Экспериментальные исследования древесины выявили, что в зависимости от уровня напряжений работа древесины при длительной нагрузке характеризуется как линейной, так и нелинейной ползучестью. Однако теоретического описания этих процессов до сих пор представлено не было. В связи с этим, одним из важнейших направлений в расчетах деревянных конструкций является составление уравнений нелинейной ползучести для различных видов напряженно-деформированного состояния деревянных стержней.
Теория нелинейной ползучести древесины
В работе А.С. Вареника и К.А. Вареника [1] на основе обработки экспериментальных данных различных ученых была обнаружена существенная нелинейность ползучести древесины и получены аналитические выражения характеристик ползучести в зависимости от уровня напряжений.
До настоящего времени, в основном, использовалось описание ползучести уравнением А.Р. Ржаницына. Предложения А.Р. Ржаницына по замене вопроса о нелинейной ползучести различными вариантами линейных задач ползучести вызвало отрицательную реакцию А.А. Гвоздева [2]. Испытывая на ползучесть какой-либо образец даже при высоких напряжениях, можно отчетливо наблюдать затухающие деформации, которые, однако, перестают быть пропорциональными напряжениям, т.е. становятся нелинейными, а это нельзя отобразить, идя по пути, предложенному А.Р. Ржаницыным. Таким образом, метод можно назвать достаточно приближенным.
При построении уравнения линейной ползучести был использован принцип наложения Больцмана, ввиду линейной связи между напряжениями σ и деформациями εМ и εП (мгновенными деформациями и деформациями ползучести):
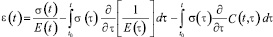, (1)
где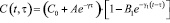 
;
C0=2,87·10-5 (МПа)-1, A=10,95 (МПа)-1; B1=1; γ=γ1=0,15 (1/сут).
В 1983 году Н.Х. Арутюнян показал, что принцип наложения может применяться и для нелинейной ползучести древесины и полимерных материалов [6]. В частности, Н.Х. Арутюнян указал, что принцип суперпозиции применим независимо от того, накапливаются в процессе ползучести необратимые деформации или все деформации ползучести полностью необратимы.
Учитывая обработку экспериментальных данных по нелинейной ползучести древесины и развивая подход И.Е. Прокоповича, В.А. Зедгенидзе [3] и А.С. Согояна [4], используем для записи теории ползучести древесины уравнение нелинейной ползучести Н.Х. Арутюняна [5]:
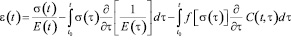, (2)
где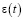 
– относительная деформация к моменту времени t под действием напряжения, приложенного в некотором возрасте τ.
Н.Х. Арутюнян отмечает, что теория ползучести в виде (2) не претендует на абсолютную точность, но может оказаться эффективной при решении прикладных задач.
Если положить, что модуль мгновенной деформации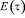 
не зависит от возраста τ (т.е. если не учитывать процесса старения материала), то 
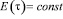. Это позволяет пренебречь вторым слагаемым в правой части (2). В результате имеем:
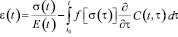. (3)
Известно, что мера ползучести С(t,τ) и характеристика ползучести φ(t,τ) связаны между собой соотношением:
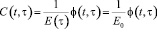. (4)
В области нелинейной ползучести Н.Х. Арутюнян ввел предположение о существовании связи:
εП=f[σ]·С(t,τ), (5)
где εП – деформация ползучести.
По аналогии с этим, введем предложение о связи:
εП=φ[σ]·φ(t,τ). (6)
Отсюда получаем уравнение связи нелинейных функций:
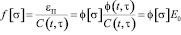. (7)
При учете старения древесины по Н.Х. Арутюняну, характеристика ползучести:
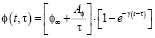. (8)
При учете старения древесины по И.Е. Прокоповичу, характеристика ползучести записывается в виде:
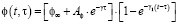. (9)
Переменность во времени модуля упругости древесины можно установить из следующих соображений.
В нормах СНиП II-25-80 «Деревянные конструкции» на основании экспериментов установлено, что величина
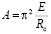(10)
является постоянной величиной, равной 3000.
В многочисленных экспериментах, проведенных Е.Н. Квасниковым [7] и Н.Л. Леонтьевым [8], установлено, что прочности древесины при сжатии Rc и растяжении Rp являются величинами, зависящими от времени. Зависимость можно представить в виде формулы:
R=a1–b1lgt, (11)
где t – время в сутках.
Например, при сжатии: Rc = 544–90lgt при влажности 20 %; Rc = 373–41lgt при влажности 56 %; Rc = 290–24lgt при влажности 62 %.
В соответствии с (10) и ввиду переменности R(t) модуль упругости E древесины также является величиной, зависящей от времени.
Однако с целью упрощений решения задач и, следуя зависимости (10), будем считать, что модуль упругости древесины E0 и прочность R не зависят от времени.
Ввиду изложенного уравнение нелинейной ползучести Н.Х. Арутюняна для древесины запишем в упрощенном виде:
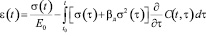. (12)
С целью получения значения коэффициента ползучести древесины βД для древесины и для использования экспериментальных данных запишем выражение для деформации ползучести:
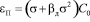, (13)
и характеристики ползучести:
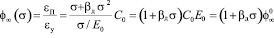. (14)
На основе обработки результатов экспериментов по ползучести древесины, в работе [1] для сжатия получено аппроксимирующее уравнение:
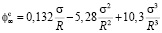. (15)
График уравнения (15) представлен на рисунке.
Полагаем, что при уровне загружения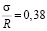 
(и ниже) наблюдается линейная
ползучесть с предельной характеристикой ползучести, равной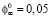 
(см. рисунок).
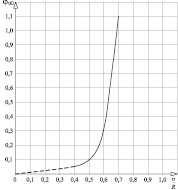
Аппроксимирующая кривая предельных значений характеристик ползучести φ∞ в зависимости от уровня напряжения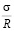 
При этом же коэффициент βД = 0 и из (13) εП = σС(t,τ).
Далее подставим в выражение (14) данные эксперимента: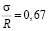 
; 
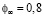. Имея
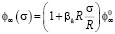, (16)
находим:
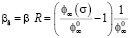(17)
и значение β1=22,38.
Если принять в соответствии с предложением К.П. Пятикрестовского и другими экспериментальными данными, что R = 550 кг/см2 (σПП = 55 МПа), то осредненный коэффициент βд для древесины в нелинейной теории Н.Х. Арутюняна следует принимать равным βд = 0,041.
Уравнение нелинейной ползучести древесины запишем в виде:
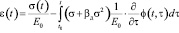, (18)
где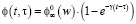 
.
Принимая значение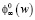 
не зависящим от времени (w – влажность в %), имеем основное уравнение нелинейной ползучести древесины:
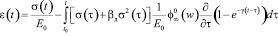. (19)
В этом уравнении можно учитывать зависимость модуля упругости древесины от влажности w, подставляя в него соответствующую эмпирическую формулу:
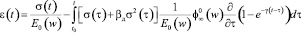. (20)
Уравнения нелинейной ползучести древесины при различных видах напряженно-деформированного состояния
Нелинейные уравнения (19) и (20) можно применять для работы древесины при сжатии, растяжении, изгибе. Отличия будут состоять в численных значениях коэффициентов βд и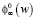 
. В этих уравнениях не учитывается старение древесины. Для учета старения необходимо использовать функции старения (8) либо (9).
Известно, что выражение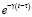 
, стоящее под интегралом в уравнении (19), позволяет преобразовать его в дифференциальное уравнение, более удобное в решении ряда практических задач расчета деревянных конструкций.
Уравнение (19) дифференцируем по времени t:
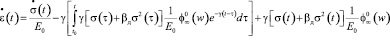. (21)
Из полученного результата находим значение интеграла, стоящего в квадратных скобках:
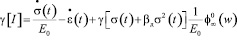. (22)
Подставляя это значение в первоначальное уравнение (19), избавляемся от интеграла и получаем основное уравнение нелинейной ползучести древесины в виде дифференциального уравнения:
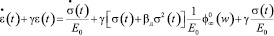. (23)
При низких уровнях загружения (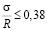
для сжатой древесины) записываем уравнение линейной ползучести древесины, полагая βд = 0:
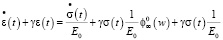. (24)
Для решения простейших задач изгиба в условиях нелинейной ползучести Н.Х. Арутюнян предлагает упростить уравнение (2), отбрасывая в правой части уравнения (23) первое и третье слагаемые. Уравнение нелинейной ползучести древесины существенно упрощается:
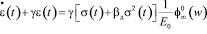. (25)
В теории ползучести такое уравнение соответствует использованию модели Фойгта с нелинейной силой.
Аналогичным приемом можно преобразовать уравнение линейной ползучести
древесины Е.Н. Квасникова:
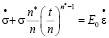, (26)
подставляя в него нелинейную функцию напряжений, полученную в данной работе:
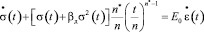. (27)
Уравнение (27) в большей степени подходит для решения задач изгиба деревянных балок.
Уравнение же (25) является более удобным для решения задач циклического загружения деревянных конструкций, в том числе для задач колебаний.
Для решения же задач расчета сжатых деревянных стоек уравнения (25) и (27) не годятся. В этом случае необходимо использовать полное уравнение нелинейной ползучести древесины (23).
Н.Х. Арутюнян указывает, что предложенная им теория нелинейной ползучести не претендует на абсолютную точность, но является эффективной при решении прикладных задач расчета конструкций.
При решении самых простейших задач расчета деревянных конструкций в условиях нелинейной ползучести можно применять теорию старения в форме, предложенной Е.Н. Квасниковым, дополнив ее нелинейной составляющей, полученной выше автором диссертации. Окончательно можно записать:
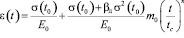, (28)
где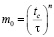 
, либо численные значения этого коэффициента, указанные для древесины Е.Н. Квасниковым.
Для случаев, учитывающих старение древесины, воспользуемся уравнением И.Е. Прокоповича и В.А. Зедгенидзе, уточнив его учетом функции нелинейной ползучести древесины. Основное уравнение в этом случае запишем в виде:
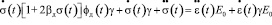, (29)
где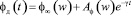 
– функция старения древесины по И.Е. Прокоповичу.
Выводы
- Экспериментальные данные по кривым характеристик ползучести древесины указывают на необходимость учета нелинейной ползучести. Обработка этих данных, а также работ известных ученых позволила описать теорию нелинейной ползучести.
- В результате работы были получены уравнения нелинейной ползучести древесины при различных напряженно-деформированных состояниях с учетом ее старения и изменения влажности. Данные уравнения можно использовать при расчетах деревянных конструкций.
Рецензенты:
Бондаренко Е.А., д.т.н., проректор по научной работе, ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород;
Санжаровский Р.С., д.т.н., профессор кафедры «Строительные конструкции», ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород.
Работа поступила в редакцию 08.08.2014.