Задача кластеризации является одной из важнейших задач интеллектуального анализа данных в различных проблемных областях – технических, естественнонаучных, социальных. Кластеризация является примером задачи обучения без учителя и сводится к разбиению исходного множества объектов на подмножества классов таким образом, что элементы одного класса были бы схожи между собой, а элементы различных классов были бы максимально различны [2].
Основной сложностью применения классических методов кластеризации для решения практических задач является то, что многие реальные объекты могут быть описаны исключительно нечеткими параметрами. В связи с этим для кластеризации подобных объектов в последнее время активно развиваются методы нечеткой кластеризации [3]. Исследованиям в данной области посвящены работы известных зарубежных и российских ученых: Bezdek J.C., Pedrycz W., Zadeh L.A., Аверкина А.Н., Батыршина И.З., Вагина В.Н., Вятченина Д.А., Ярушкиной Н.Г. и др.
Целью исследования является разработка модели, метода и комплекса программ концептуальной кластеризации объектов, характеризуемых нечеткими параметрами, на основе классического метода кластеризации COBWEB. Эффективность разрабатываемого метода концептуальной кластеризации определяется его способностью работать с объектами, характеризуемыми параметрами с нечеткими значениями, и достигаемой точностью кластеризации.
Материалы и методы исследования
В настоящее время известно множество алгоритмов нечеткой кластеризации, таких как Fuzzy C-Means, FOPTICS и др. [7]. Данные алгоритмы формируют кластеры, границы которых размыты, а объект может принадлежать более чем одному кластеру с различными степенями принадлежности. Однако следует отметить, что большинство алгоритмов нечеткой кластеризации работают с четкими значениями параметров объектов, формируя кластеры, например, на основе оценки расстояний между объектами и центром кластера. Такой подход не позволяет эффективно осуществлять кластеризацию объектов с нечетко заданными значениями параметров. В связи с этим актуальной задачей является разработка методов кластерного анализа, способных учитывать нечеткую природу объектов, то есть работать с параметрами, заданными в нечеткой форме в виде функций принадлежности.
Для решения многих практических задач в настоящее время используется концептуальная кластеризация данных, ярким представителем которой является метод COBWEB [6]. Классический вариант реализации метода COBWEB не предполагает работу с параметрами, заданными в нечеткой форме, что актуализирует решение поставленной выше задачи для данного метода.
Для формализации метода кластеризации COBWEB, обозначим через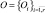 
– множество распознаваемых объектов, характеризуемое бинарными параметрами 
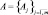, принимаемыми одно из возможных значений 
. 
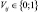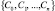– множество формируемых кластеров, где n – заранее неизвестно.
Полезность кластеризации в методе COBWEB рассматривается как функция CU, определяющая сходство объектов в рамках одного кластера, и их различие по отношению к объектам из других кластеров. Внутриклассовое сходство определяется условной вероятностью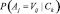 
, а межклассовое сходство условной вероятностью 
.
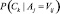Функция полезности кластеризации определяется согласно [6] в виде
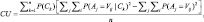(1)
где n – количество кластеров.
Метод COBWEB строит дерево классификации с вероятностными описаниями концептов. Выбор возможного способа кластеризации объектов основан на значениях функции полезности кластеризации (1). При построении дерева классификации используются следующие 4 операции [6]:
- отнесение объекта к наилучшему из существующих кластеров;
- добавление нового кластера, содержащего единственный объект;
- слияние двух существующих кластеров в один новый с добавлением в нее этого объекта;
- разбиение существующего кластера на два и отнесение объекта к лучшему из вновь созданных кластеров.
Предлагается модель концептуальной кластеризации объектов в виде дерева, представленного на рис. 1.
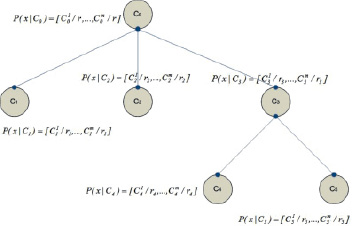
Рис. 1. Модель концептуальной кластеризации
Где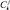 
– количество раз, когда значение параметра Aj = 1 для объектов в кластере Ck, rk – количество объектов в кластере Ck.
Пошаговое описание метода концептуальной кластеризации:
1. Вводится корневой кластер С0, свойства которого совпадают со свойствами первого объекта О1 = [V11, …, V1m]. Для каждого последующего объекта Оi = [Vi1, …, Vim] выполняется цикл, реализующий шаги 2‒6, в рамках которых выполняются 4 выше представленные операции.
2. Объект Оi добавляется поочередно в кластеры С1, C2,…, Сk. После каждого добавления вычисляется полезность кластеризации СU1,…, СUk.
3. Для объекта Оi создается новый кластер Сk + 1, объект помещается в кластер и вычисляется полезность кластеризации CUk + 1.
4. Объединяются два кластера с максимальными значением полезности кластеризации из СU1, …, СUk. Образуется новый кластер, в него добавляется объект Оi. Вычисляется полезность кластеризации CUk + 2.
5. Объект Оi добавляется в кластер с максимальным значением полезности кластеризации из СU1 ,…, СUk. Образуется новый кластер с двумя кластерами-потомками. Вычисляется полезность кластеризации CUk + 3.
6. Выбирается максимальное значение полезности кластеризации среди полезностей СU1,…, СUk,CUk + 1, CUk + 2, CUk + 3, в соответствии с ним выбирается операция разбиения объектов по кластерам.
В статье предложена модификация метода концептуальной кластеризации, основанная на методе COBWEB, позволяющая работать с объектами, характеризуемыми нечеткими параметрами. Данный метод предполагает реализацию классического метода концептуальной кластеризации COBWEB в следующих условиях:
1. Множество распознаваемых объектов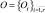 
, характеризуется нечеткими параметрами 
.
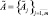2. Значение параметра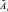 
для объекта Оi определяется в виде функции принадлежности 
.
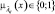3. Степень сходства двух функций принадлежност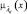и 
и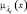 
определяется их наибольшей верхней границей [5] в виде
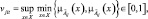(2)
где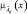 
– функция принадлежности параметра 
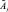для объекта Оi, а 
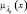– функция принадлежности параметра 
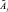для объекта Оt.
4. Основываясь на формуле полезности кластеризации (1) классического метода COBWEB и условиях 1–3, оценка полезности кластеризации осуществляется по модифицированной формуле 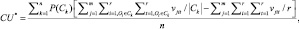(3)
(3)
где n – количество кластеров.
Также были проведены численно-параметрические исследования разработанного метода по отношению к используемым функциям принадлежности. Рассмотрено два основных типа функций принадлежности: кусочно-линейные и П-образные[1].
Наибольшая верхняя граница П-образных функци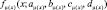й 
и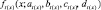 
может быть представлена в виде точки пересечения S-образных функци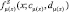й 
и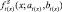 
[1]. Исходя из способа задания П-образных функций принадлежности, точку пересечения П-образных функций принадлежности можно представить как
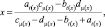(4)
Исходя из (4) получаем степень сходства функций принадлежност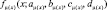и 
и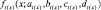 
.
Пересечение двух кусочно-линейных функций принадлежности, исходя из способа задания кусочно-линейных функций принадлежности, определяется как
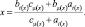(5)
Исходя из (5), получаем степень сходства функций принадлежности.
Выбор типа функции принадлежности основан на практических результатах, полученных при решении задачи кластеризации конкретных объектов. Экспериментальным путем показано, что определение значений параметров объектов в виде кусочно-линейных функций принадлежности позволяет увеличить разделяющую способность кластеров в разработанном методе по сравнению c П-образными функциями. Таким образом, использование кусочно-линейных функций принадлежности для описания нечетких параметров объектов более предпочтительно по сравнению с П-образными функциями.
Результаты исследования и их обсуждение
В качестве примера была решена задача автоматизации формирования пользовательских ролей [4] на действующей информационной системе конкретной организации. Осуществлялась кластеризация 22 пользователей: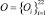 
. Для описания поведения пользователей было выделено 18 параметров 
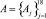. На основании анализа поведения пользователей по выделенным параметрам осуществлялась кластеризация и распределение пользователей по кластерам. В результате кластеризации было выделено 10 кластеров. Данные кластеры содержали пользователей в соответствии с их функциональными обязанностями. Также было выделено два кластера с аномальным поведением пользователей.
Решение данной задачи позволяет, с одной стороны, значительно упростить работу администратора информационной безопасности по формированию пользовательских ролей в ИС, с другой стороны, позволяет обнаруживать аномальное поведение пользователей в ИС, выявляя недобросовестных сотрудников, использующих информационные ресурсы организации не только для выполнения своих функциональных обязанностей, но и в личных целях.
Вторая практическая задача, решенная с помощью разработанного метода концептуальной кластеризации, стояла в распределении животных по кластерам на основе их параметров, заданных в нечетком виде. Для каждого семейства животных (медвежьи, зайцевые, кошачьи) взята выборка по 7 видов –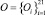 
. Каждое животное было описано 3 параметрами, описанными в нечетком виде (длина тела, вес, скорость) – 
.
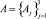В результате работы разработанного метода концептуальной кластеризации объекты были распределены по 3 кластерам в соответствии с семействами животных. На примере решения данной задачи разработанный метод нечеткой концептуальной кластеризации показал 100 % точность кластеризации.
Для сравнительного анализа данная задача также была решена с помощью известных методов кластеризации EM и g-means. При этом выполнялась дефазификация параметров объектов, заданных в нечетком виде. Результаты сравнительного анализа точности кластеризации методов представлены на рис. 2.
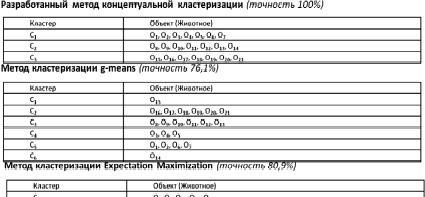
Рис. 2. Сравнительный анализ методов кластеризации
Таким образом, видим, что точность решения задачи кластеризации методами EM и g-means составила соответственно 89 и 76,1 %, что меньше точности, полученной в результате работы разработанного метода.
Заключение
Разработанный метод концептуальной кластеризации, в отличие от существующих методов кластеризации, позволяет работать с объектами, характеризуемыми нечеткими параметрами, и строить модель концептуальной кластеризации для объектов нечеткой природы. Основу метода составляет предложенная в работе модифицированная формула оценки полезности концептуальной кластеризации для объектов, характеризуемых нечеткими параметрами. Экспериментальным путем показано, что использование кусочно-линейных функций принадлежности для задания значений нечетких параметров объектов позволяет увеличить разделяющую способность кластеров в разработанном методе по сравнению с П-образными функциями. Полученные в работе теоретические результаты были использованы для решения задачи автоматизации формирования пользовательских ролей в корпоративной информационной сети, включающей в себя 22 пользователя, каждый из которых описывался 18 параметрами. Полученные результаты позволили выделить пользователей, характеризующихся аномальным поведением в компьютерной сети. На примере решения задачи кластеризации разработанный метод показал 100 % точность. На тех же данных точность известных методов кластеризации EM и g-means составила соответственно 89 и 76,1 %.
Рецензенты:
Райхлин В.А., д.ф.-м.н., профессор кафедры «Компьютерные системы», ФГБОУ ВПО «КНИТУ им. А.Н. Туполева – КАИ», г. Казань;
Захаров В.М., д.т.н., профессор кафедры «Компьютерные системы», ФГБОУ ВПО «КНИТУ им. А.Н. Туполева – КАИ», г. Казань.
Работа поступила в редакцию 15.07.2014.