Несмотря на то, что изучению структуры материалов в стеклообразном состоянии посвящено огромное количество работ, до сих пор не существует универсальной модели, которая бы полностью описывала данные системы [10, 15]. Один из подходов к решению задачи по созданию такой модели лежит в области компьютерного моделирования атомной структуры областей ближнего упорядочения. Он заключается в построении моделей структуры материалов в стеклообразном состоянии и расчете соответствующих теоретических дифракционных картин для их сравнения с экспериментом. В предыдущей работе [6] было проведено рентгенографическое исследование методом Уоррена – Финбака образцов ксерогелей, полученных из водного раствора щелочного силиката при модифицировании кобальтом, никелем и титаном.
В методе Уоррена – Финбака [1, 14] характеристики ближнего порядка определяются исходя из предположения, что система является гомогенной (с однородным на наноуровне распределением в пространстве и химического состава, и структурной организации материала). Проводится сравнение характеристик ближнего порядка с величинами, определяемыми для кристалла, у которого однородность постулируется: пространство заполняется путем трансляции одной и той же элементарной ячейки. В работе [6] было обнаружено несоответствие характеристик ближнего порядка в исследуемых образцах с таковыми в кристаллических фазах того же химического состава. Возможная причина этого – возникновение концентрационных неоднородностей по катионам (Na, Co и др.) на субнанометровом уровне.
В данной работе предпринята попытка описания этих неоднородностей (как по составу, так и по структурной организации областей ближнего упорядочения) в рамках модели механической смеси ультрамалых кристаллитов различной природы. Рассмотрение ведется на примере образцов исходного и модифицированного кобальтом ксерогеля на основе жидкого стекла (ЖС).
Построение моделей областей ближнего упорядочения исходного образца ксерогеля
В ряде случаев получить информацию об атомном строении рентгеноаморфных объектов можно путем расчета кривых распределения интенсивности рассеяния рентгеновских лучей скоплением атомных кластеров различных размеров и формы и сопоставления рассчитанных для моделей кривых с дифракционными картинами, полученными из рентгенографического эксперимента [4]. Используя данный подход и опираясь на предыдущую работу [6], в которой было установлено, что в исходном состоянии характер ближнего упорядочения ЖС подобен порядку в кристаллической фазе Na2Si3O7 [11], была подобрана модель, соответствующая структурной организации образца исходного ксерогеля. Модель представляет собой совокупность хаотически разориентированных кристаллитов, имеющих размер одной элементарной ячейки Na2Si3O7 (кластеры из 48 атомов: 8 Na, 12 Si, 28 O; размер кластеров приблизительно 6×10×10 Å3). На рис. 1 приведены кривые распределения интенсивности рассеяния I(S) экспериментальным образцом (a) и сформированным модельным объектом (b). Методика расчета распределения интенсивности рассеяния рентгеновских лучей совокупностью разориентированных кластеров атомов описана в работе [4]. Оценка качества модели производилась с помощь профильного фактора недостоверности, который рассчитывался по формуле:
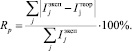(1)
Для данного варианта модели структуры профильный фактор недостоверности составил 7,8 %.
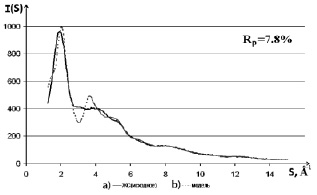
Рис. 1. Кривые распределения интенсивности рассеяния (в электронных единицах) для исходного образца ксерогеля (a) и кластера, имеющего размер одной элементарной ячейки Na2Si3O7 (координаты атомов взяты из работы [11]) (b)
Анализ кривых, представленных на рис. 1, показывает, что в областях значений модуля дифракционного вектора S от 1,2 до 2,6 Å–1 и от 5 до 15 Å–1 расхождение между теоретической и экспериментальной рентгенограммой минимально, однако в области значений S от 2,2 до 4 Å–1 теоретическая кривая рассеяния осциллирует около экспериментальной. Было сделано предположение о химической микронеоднородности исследуемых образцов [2] и сформированы ультрамалые (размеры составляли одну или несколько элементарных ячеек) кристаллиты со структурой различных фаз, из которых предположительно может состоять в среднем область ближнего упорядочения образца. Для исходного ЖС это были Na2Si3O7, SiO2 (кристобалит и тридимит), Na2Si2O5 (a- и β-модификации). Координаты атомов для построения кластеров были взяты из базы данных ICSD [9]. Структура формировалась в рамках модели «механической смеси», а итоговая картина рассеяния – путем суммирования отдельных составляющих, и в процентном отношении приведенная на формульную единицу. Наилучшего результата удалось достичь при содержании в облучаемом объеме образца 80 % Na2Si3O7, 10 % SiO2 (3 % кристобалит и 7 % тридимит), 8 % – a-Na2Si2O5 и 2 % – β-Na2Si2O5. Все указанные кристаллиты имеют размеры одной элементарной ячейки за исключением кристаллита SiO2 (кристобалит), размер которого составляет 2×2×2. Результат в виде кривых I(S) экспериментального образца (a) и от сформированного модельного объекта (b) приведен на рис. 2. Рассчитанный для данного варианта модели структуры фактор недостоверности составил 5,9 %. Осцилляции в указанной выше области на кривой, рассчитанной для модели, сохранились, хотя и уменьшились. Следовательно, введения в модель неоднородностей в виде наличия в матрице ЖС кристаллитов SiO2 и Na2Si2O5 недостаточно.
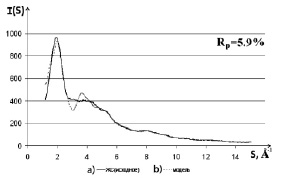
Рис. 2. Кривые распределения интенсивности рассеяния (в электронных единицах) для исходного образца ксерогеля (a) и модельного объекта, представляющего собой совокупность хаотически разориентированных кластеров состава Na2Si3O7, SiO2 и Na2Si2O5 (b)
Из зависимостей интенсивности рассеяния I(S) от длины дифракционного вектора S = (4spinq)/l, полученных в широком угловом интервале, рассчитывались функции H(s) [1]:
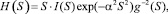(2)
где i(s) интерференционная функция рассеяния, exp(–a2S2) – множитель затухания. g(S) – коэффициент обострения, обуславливающий повышение контрастности интерференционной картины при больших значениях S. Физически введение фактора g-2(S) означает замену функций атомного рассеяния f(S) на число рассеивающих электронов в атоме (т.е. замену «размазанного» электронного облака на точечный заряд, равный Ze и помещённый в центр масс облака). Это стандартный прием, используемый в Паттерсоновском анализе монокристаллов [5].
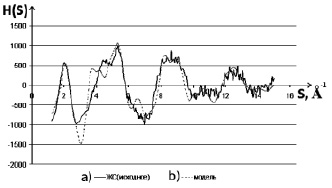
На кривых распределения S-взвешенной интерференционной функции H(S) более ярко выражены различия в дифракционной картине, чем на кривых распределения I(S). На рис. 3 приведены кривые H(S) для исходного образца ксерогеля (a) и модельного объекта, представляющего собой совокупность хаотически разориентированных кластеров состава Na2Si3O7, SiO2 и Na2Si2O5 (b). На рассчитанной для модели кривой H(S) наблюдается расхождение кривых в области 2,7–5 Å–1 и присутствует небольшой максимум в районе S ~ 6,6 Å–1, в остальном ход рассчитанной для модели кривой качественно повторяет экспериментальную. Использование профильного фактора недостоверности для оценки качества модели в данном случае затруднительно из-за достаточно высокого уровня статического шума на кривой H(S). Rp = 15 % – это минимально возможный R-фактор в данном случае. В связи с этим для анализа степени совпадения теоретической и экспериментальной кривых H(S) целесообразнее использовать коэффициент детерминации (R2), который применяется при оценке качества регрессионных моделей. Чем R2 ближе к 1, тем удачнее регрессионная модель. Вычисление R2 производилось по формуле [7]:
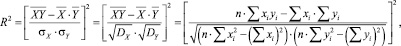(3)
где R – коэффициент корреляции;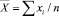 
– среднее значение Hэксп(S); 
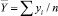– среднее значение Hтеор(S); 
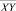– среднее значение произведения Hэксп(S)∙Hтеор(S); 
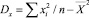– дисперсия X; 
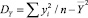– дисперсия Y; 
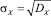– среднеквадратичное отклонение X; 
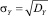– среднеквадратичное отклонение Y.
Для данной модели значение R2 составило 0,82, что свидетельствует о достаточно хорошей степени совпадения.
Далее численным интегрированием функции H(S) рассчитывали кривую распределения парных функций D(r) [1]:
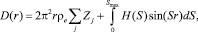(4)
где ρe – средняя электронная плотность, Zj – атомный номер j-го элемента, входящего в состав исследуемого материала.
Количественное сопоставление кривых распределения парных функций D(r), рассчитанных из H(S) для модели, с кривой, полученной из экспериментальных значений Н(S), затруднено. Причиной служит зависимость D(r), рассчитанной для модели, от размеров и формы кластера, поэтому более корректно проводить это сопоставление на уровне радиального распределения плотности вероятности W(r) = D(r)/D0(r), где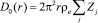 
в случае бесконечной среды. А в случае кластера конечных размеров D0(r) – плавная кривая, рассчитанная из значений интерференционной функции H(S) в интервале S от 0,01 до Smin, т.е. в области малоуглового рассеяния рентгеновских лучей [8].
На рис. 4 показаны функции радиального распределения плотности вероятности W(r), рассчитанные для исходного образца ксерогеля (a) и модельного объекта, представляющего собой совокупность хаотически разориентированных кристаллитов состава Na2Si3O7, SiO2 и Na2Si2O5 (b). Из сравнения кривых видно, что до r = 3,5 Å кривые W(r) хорошо коррелируют друг с другом. Это свидетельствует о том, что в экспериментальном образце сохраняются структурные мотивы соответствующих кристаллических фаз на расстояниях, равных первым координационным сферам Si–O, Na–O, O–O, Si–Si и Na–Na. Однако при r ~ 2,3 Å и в области r от 3,5 до 5 Å наблюдается расхождение в величине максимумов на кривых W(r). Это означает, что степень упорядочения в расположении атомов модели чуть выше, чем в образце ксерогеля.
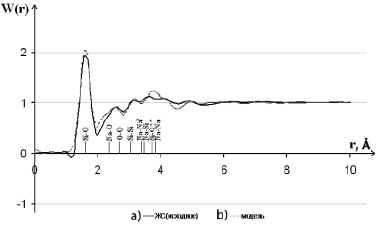
Рис. 4. Функции радиального распределения плотности вероятности W(r) для исходного образца ксерогеля (a) и модельного объекта, представляющего собой совокупность хаотически разориентированных кластеров состава Na2Si3O7, SiO2 и Na2Si2O5 (b). Штрихами обозначены рассчитанные из эксперимента в [6] радиусы координационных сфер (Na–Na* – объединённая сфера Na–O, Na–Na и O–O; Si–O** – объединенная сфера Si–O и Na–O)
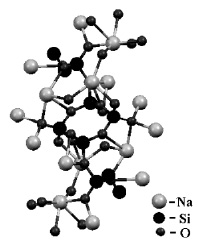
Рис. 5. Элементарная ячейка Na2Si3O7 [11]
Анализ кристаллической структуры Na2Si3O7 (рис. 5) показал, что она содержит (в пределах элементарной ячейки) четыре тетраэдра SiO4, соединенные в кольцо вершинами через общий атом кислорода. К третьему атому кислорода каждого тетраэдра присоединен тетраэдр SiO4 (из другого кольца). К четвертому атому кислорода присоединен ион Na, соседями которого являются 5 ионов кислорода, принадлежащие другим тетраэдрам. Анализ межатомных расстояний в кристаллической структуре Na2Si3O7 показал, что вклад в максимум при r = 3,8 Å на модельной кривой W(r) (рис. 4) вносят пары атомов Na–Na, Na–Si и Si–O. В образце ксерогеля (в отличие от монокристалла Na2Si3O7 ) возможны концентрационные неоднородности в распределении натрия. Нарушения равномерности в расположении натрия приводят к увеличению разброса в межатомных расстояниях пар Na–Na, Na–Si и, как следствие, к возрастанию беспорядка в разворотах тетраэдров SiO4. В результате максимум на W(r), соответствующий паре Si–O, сильно размывается. Таким образом, максимум при r = 3,8 Å и минимум при r = 4,5 Å на кривой W(r) модели являются следствием неучёта случайного разворота структурных элементов (в основном тетраэдров SiO4) друг относительно друга.
Построение моделей областей когерентного рассеяния ксерогеля на основе ЖС, модифицированного кобальтом
Следуя методике, описанной выше, для образца ксерогеля на основе ЖС, модифицированного кобальтом, были сформированы кластеры ультрамалых кристаллитов различных фаз, из которых предположительно может состоять образец. На основании сравнения картин рассеяния, рассчитанных для моделей с экспериментальной кривой, было установлено, что модель «механической смеси» состоит из кристаллитов состава Na2Si3O7, SiO2 (кристобалит и тридимит) и Na2Si2O5 (a- и β-модификации) и оксида кобальта CoO двух полиморфных модификаций (типа NaCl [12] и типа вюрцита [13]). Далее варьировалось процентное соотношение количества кристаллитов в облучаемом объеме, и для каждого варианта рассчитывалась картина рассеяния моделью. В результате формульная единица модели была записана как Na2Si3O7,78Co0,78, а экспериментальная кривая нормирована на тот же состав.
Состав кластера модели:
● 61 % механическая смесь состава Na2Si3O7 (11 % – SiO2 кристобалит, 24 % SiO2 тридимит, 28 % – a-Na2Si2O5, 7 % – β- Na2Si2O5 и 30 % Na2Si3O7);
● 31 % – слой из элементарных ячеек CoO (типа вюрцита) размером 5×1×5;
● 8 % – CoO (типа NaCl) 2x2x2.
На рис. 6 приведены кривые I(S) экспериментального образца (a) и сформированного модельного объекта (b). Для данного варианта модели структуры профильный фактор недостоверности составил 5,7 %. Сравнительный анализ кривых I(S) показывает, что максимум при значении модуля дифракционного вектора S ~ 1,7 Å–1 в модели более узкий и смещён в сторону меньших значений S по отношению к положению максимума, наблюдаемому в эксперименте.
Небольшие расхождения экспериментальной кривой I(S) и кривой I(S), рассчитанной для модели, наблюдаются в диапазоне S от 3 до 7 Å–1. На рис. 7 приведены кривые H(S) для образца ксерогеля, модифицированного кобальтом (a) и модельного объекта, представляющего собой совокупность хаотически разориентированных кристаллитов Na2Si3O7, SiO2, Na2Si2O5 и CoO (b).
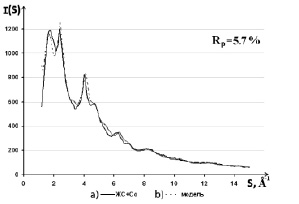
Рис. 6. Кривые распределения интенсивности рассеяния (в электронных единицах) для образца ксерогеля, модифицированного кобальтом (a), и модельного объекта (b)
Из анализа рис. 7 видно, что наибольшие расхождения теоретической и экспериментальной кривых H(S) наблюдаются в области S от 5 до 8 Å–1. На модельной кривой присутствует дополнительный пик при S ~ 5,5 Å–1, максимум при S ~ 6,3 Å–1 смещен в сторону больших значений S, а при S ~ 7,0 Å–1 – в сторону меньших. Дополнительный пик обусловлен рассеянием рентгеновских лучей от кристаллитов Na2Si3O7, SiO2 и Na2Si2O5, его отсутствие на экспериментальной кривой может быть объяснено несколькими возможными причинами. Первое, это более высокий порядок в расположении атомов в указанных модельных кластерах, чем в образце. Второй причиной может быть погасание максимума в результате наложения картин рассеяния от двух различных фаз. Третьей – неучет возможной неравноосности модельных кристаллитов. Для устранения данной неоднозначности необходимы дополнительные исследования. Степень совпадения экспериментальной и модельной кривых H(S) оценивали с помощью коэффициента детерминации (R2). Для данной модели значение R2 составило 0,71.
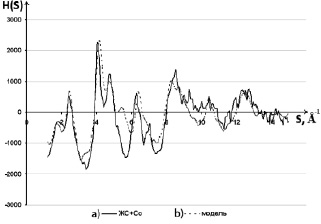
Рис. 7. S-взвешенные интерференционные функции рассеяния для образца ксерогеля, модифицированного кобальтом (a), и модельного объекта (b)
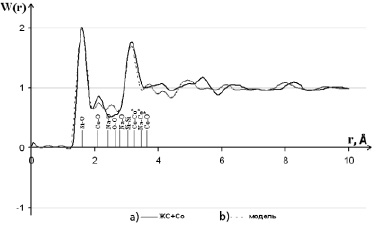
Рис. 8. Функции радиального распределения плотности вероятности W(r) для образца ксерогеля, модифицированного кобальтом (a), и модельного объекта (b). Штрихами рассчитанные из эксперимента в [6] радиусы координационных сфер (* отмечены объединенные сферы)
Анализ функций W(r) (рис. 8) показывает, что модель, представляющая собой совокупность хаотически разориентированных кристаллитов состава Na2Si3O7, SiO2, Na2Si2O5 и CoO, хорошо описывает расположение атомов в пределах первых координационных сфер (до r ≈ 3,6 Å). Небольшие расхождения в величине максимумов на W(r), соответствующим первым координационным сферам Co–O, Na–O и O–O, обусловлены нарушением равномерности в распределении Na в образце по сравнению с моделью. Осцилляции на кривых W(r) затухают при одинаковых значениях r ~ 9 Å, следовательно, дальность корреляции в расположении атомов в экспериментальном образце и модельном объекте одна и та же. При этом необходимо обратить внимание на «систематическое» смещение максимумов экспериментальной W(r) при r > 5 Å в сторону больших значений межатомных расстояний по сравнению с модельной.
Заключение
Модель хаотически ориентированных ультрамалых кристаллитов описывает структуру исследуемых ксерогелей на основе жидкого стекла в пределах первых координационных сфер. Показано, что неоднородности, как по составу, так и по структуре можно обсуждать на основе модели механической смеси кристаллитов различного состава и формы. Полученные в работе данные о фазовом составе смеси кристаллитов качественно согласуются с исследованиями образцов проведенными с помощью ИК-спектроскопии и просвечивающей электронной микроскопии [3].
Авторы выражают глубокую признательность Е.Ф. Кудиной (доктор технических наук, доцент, Институт механики металлополимерных систем НАН Беларуси) за предоставленные образцы и Л.А. Алешиной (кандидат физико-математических наук, доцент, Петрозаводский государственный университет) за ценные замечания и предложения.
Исследования проведены в рамках реализации программы стратегического развития на 2012–2016 годы «Университетский комплекс ПетрГУ в научно-образовательном пространстве Европейского Севера: стратегия инновационного развития».
Рецензенты:
Стефанович Г.Б., д.ф.-м.н., профессор, заведующий кафедрой информационно-измерительных систем и физической электроники, Петрозаводский государственный университет, г. Петрозаводск;
Белашев Б.З., д.т.н., ведущий научный сотрудник лаборатории геофизики, Институт геологии Карельского научного центра РАН, г. Петрозаводск.
Работа поступила в редакцию 28.07.2014.