Для получения двухфазных систем жидкость – твердые частицы широко используются аппараты роторного типа [1]. Процесс диспергирования может происходить как с изменением размеров твердых частиц, так и без их изменения. В данной работе рассматривается процесс получения двухфазной системы жидкость – твердые частицы с учетом дезагрегации твердых частиц.
Процесс получения двухфазной системы жидкость – твердые частицы в аппарате роторного типа осуществляется в следующей последовательности. Вначале в рабочую емкость вводят жидкий компонент. Затем при медленном вращении вводят порошкообразный компонент. Затем скорость вращения вала резко увеличивают до образования воронки (эффект Dougnut). Расчетная схема движения представлена на рис. 1.
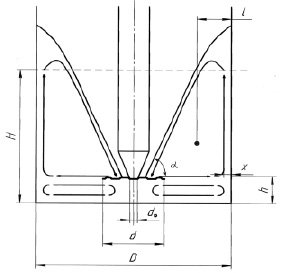
Рис. 1. Расчетная схема движения в аппарате роторного типа
Для удобства описания процесса смешения перейдем в систему координат, вращающуюся вместе с валом. В выбранной системе координат при вращении турбинной мешалки выделяются два циркуляционных контура: верхний и нижний (рис. 1). Верхний циркуляционный контур можно аппроксимировать в виде треугольника. Соответственно, линии тока в данном контуре будут представлять собой также треугольники.
Процесс смешения происходит преимущественно в верхнем и контуре за счет случайного блуждания частиц твердой фазы в направлении, перпендикулярном к направлению потока. В силу геометрии задачи площадь поверхности циркуляционного контура складывается из площадей поверхностей горизонтального диска, вертикальной цилиндрической обечайки и усеченного конуса, величина которых зависит от координаты x. Для удобства эту координату будем отсчитывать от стенки аппарата.
Поток массы твердых частиц через поверхность циркуляционного контура определяется выражением [2]:
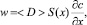(1)
где c – концентрация твердой фазы; ⟨D⟩ – среднестатистический коэффициент макродиффузии; x – координата, определяющая положение циркуляционного контура; S(x) – площадь поверхности циркуляционного контура, которая определяется уравнением
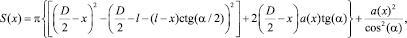(2)
где 
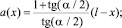
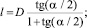
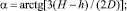(3)
l – максимальное значение координаты x, которое будет определяться центром циркуляции.
Изменение количества твердой фазы в единицу времени в циркуляционном слое толщиной dx будет определяться разностью потоков массы:
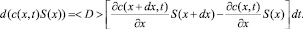(4)
Выполняя предельный переход, получим следующее уравнение:
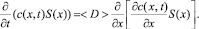(5)
Граничное условие составляется из тех соображений, что на границе циркуляционных контуров у твердой стенки перенос твердой фазы во внешнюю среду отсутствует, и записывается в виде
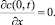(6)
Начальное условие строится из предположения, что в начале процесса твердые частицы подаются сверху на движущийся слой жидкости и, следовательно, полностью заполняют все циркуляционные контуры, граничащие со стенкой аппарата, и записывается в виде
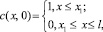(7)
где значение координаты x1 определяется из равенства
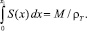(8)
Нетрудно убедиться, что уравнение (5) полностью соответствует условию сохранения массы
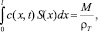(9)
где M – масса твердой фазы; ρт – истинная плотность твердой фазы.
Среднестатистический коэффициент макродиффузии ⟨D⟩ существенно зависит от размера частиц твердой фазы. Чем меньше размеры частиц твердой фазы, тем выше их подвижность в хаотическом движении. В связи с этим величина ⟨D⟩ может быть представлена в виде
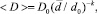(10)
где D0 – коэффициент макродиффузии при размере частиц размером d0;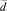 
– средний размер частиц твердой фазы, k – некоторая константа, определяемая в рамках модели. Экспериментальные исследования показывают, что величина коэффициента макродиффузии D0 определяется числом оборотов ротора и конструктивными особенностями диспергатора.
Предполагаем, что процесс смешения практически не влияет на процесс диспергирования твердой фазы, так как за счет высокой турбулентности распределение частиц по объему жидкой фазы практически равномерно.
В работе [2] показано, что процесс диспергирования твердой фазы может быть описан уравнением
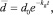(11)
где kg – коэффициент скорости диспергирования; n – константа, определяемая природой материала твердой фазы; d0 – начальный средний размер частиц твердой фазы. Параметры уравнения (10) определяются регрессионными методами на основе обработки экспериментальных данных.
Насосная производительность в верхнем контуре определяется известной формулой [1]:
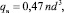(12)
где n – число оборотов ротора; d – диаметр мешалки. В соответствии с формулой (9) время движения в верхнем циркуляционном контуре будет равно
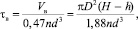(13)
где Vв – объем верхнего циркуляционного контура.
Для решения дифференциального уравнения в частных производных (5) относительно c(x, t) будем использовать численный анализ для значений x ∈ [0, l] и t ∈ [0, T] методом сеток, сделав следующие разбиения x и t с шагами, которые определяются следующими формулами:
hx = l/m; ht = τв, (14)
где m – соответственно число точек для переменных x и t, которое определяется качеством смеси, о котором будет сказано позднее; определяется формулой (13).
В соответствии с численным анализом используем приближенные выражения для производных:
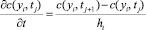(i = 0, 1, 2, ..., n; j = 0, 1, 2, ..., m); (15)
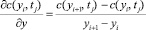(i = 0, 1, 2, ..., n; j = 0, 1, 2, ..., m); (16)
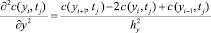(i = 0, 1, 2, ..., n; j = 0, 1, 2, ..., m). (17)
Подставляя формулы (15)–(17) в уравнение (5), получим:
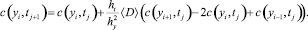(18)
Решение модели осуществляется численно стандартным сеточным методом. Время перемешивания T (число N) определяется качеством смеси, которое оценивается по величине коэффициента неоднородности:
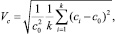(19)
где k – количество проб; ci – концентрация твердой фазы в i-м циркуляционном контуре; c0 – среднее значение концентрации твердой фазы по объему аппарата.
На рис. 2 представлено сопоставление теоретических и расчетных данных по качеству смеси при различных значениях времени процесса смешения.
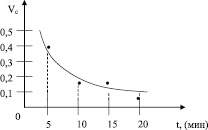
Рис. 2. Зависимость качества смешения от времени процесса перемешивания
Расчет производился для получения двухфазной системы вода ‒ кальцит с процентным содержанием кальцита 40 %. В процессе диспергирования отношение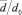 
составило 0,76. Процесс производился при следующих параметрах аппарата: D = 1,5 м, H = 2,0 м, d = 0,4 м, h = 0,15 м. При числе оборотов ротора n = 1500 об/мин коэффициент диффузии составил ⟨D⟩ = 0,57⋅10–3, k = 1,27.
Параметры модели дезагрегации твердых частиц определяются методами статистического анализа на основе экспериментальных данных в программе Statistica 6.0. В результате получено уравнение
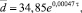(20)
где τ – время диспергирования (с).
Значение коэффициента неоднородности рассчитывалось по массе твердой фазы. Пробоотборником отбиралось 30 проб из различных точек объема смеси, положение которых определялось расстоянием от стенки аппарата. Все точки находились на одной высоте над мешалкой со значением равным величине 0,3 м. Масса кальцита в пробе определялась путем полного выпаривания воды. Дисперсность кальцита определялась микроскопическим методом. Расхождение теоретических и экспериментальных данных не превышает 12 %.
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Ярославского филиала МИИТ, г. Ярославль;
Смирнов А.Д., д.ф.-м.н., профессор Ярославского государственного университета им. П.Г. Демидова, г. Ярославль.
Работа поступила в редакцию 28.07.2014.