Лесовозный транспорт оказывает существенное воздействие на территориальное размещение лесопромышленных предприятий, на процессы специализации и кооперирования производства. Влияние его проявляется в двух направлениях. С одной стороны, транспорт выступает как производственный ресурс (ограничивающий фактор), с другой – транспортные расходы выступают как составляющая затрат и, следовательно, влияющие на размещение производства, его специализацию и кооперирование.
При учёте транспортного фактора при планировании выделяются два круга методических вопросов: как оценить существенность транспортного фактора и как формировать нормативную базу по транспорту для задач размещения и развития производства (то есть определить величины транспортных расходов по элементам транспортной сети). Чем меньше требуется дополнительных затрат на транспорт, тем относительно выгоднее большие расстояния транспортировки лесопродукции. С другой стороны, чем больше требуется затрат на транспорт, тем выгоднее сокращать дальность перевозки (целесообразнее рассредоточивать производство) [1].
Рассматриваемую проблему можно решить с помощью класса задач нелинейного программирования, представленных в виде
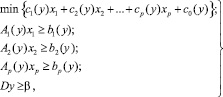 (1)
(1)
где коэффициенты целевой функции сi, технологические матрицы Аi и векторы bi являются функциями вектора связывающих переменных у. Если зафиксировать значения этих переменных, то задача (1) становится задачей линейного программирования с переменными х. Эта задача имеет блочно-диагональную структуру технологической матрицы и поэтому распадается на р независимых подзадач. Задачи подобного типа являются нелинейным обобщением блочных линейных задач со связывающими переменными. Большинство методов решения таких задач основано на идеях декомпозиции и сводится к решению последовательности линейных подзадач для различных фиксированных значений вектора у.
Задачи типа (1) часто возникают при составлении графиков производства и распределения продукции лесоперерабатывающих комплексов, когда оптимальный план составлен для целого комплекса предприятий. При планировании производства возникают следующие задачи:
1. Наилучшим образом распределить различные виды лесопродукции между ЛПК, а внутри – между технологическими установками.
2. Рационализировать материальные потоки между различными установками. (Решение задачи усложняется наличием промежуточных видов продукции, которые могут быть направлены на другие ЛПК для дальнейшей переработки.)
3. Определить оптимальные варианты, режимы использования технологических установок с учетом различных факторов и условий. Зависимость свойств потоков от этих переменных, как правило, носит ярко выраженный нелинейный характер.
4. Обосновать наилучшие схемы транспортировки лесопродукции при определенных ограничениях на объемы потребления.
5. Найти рациональный вариант закрепления потребителей за лесопромышленным комплексом ЛПК.
Все эти вопросы взаимосвязаны. Так, решение последнего зависит не только от транспортных затрат, но и от производственных мощностей по различным видам лесопродукции на предприятиях и от относительной эффективности их производства. Решение осложняется еще и тем обстоятельством, что ЛПК различаются возрастом и структурой оборудования основного и вспомогательного производств. Будем в дальнейшем плановый горизонт (период) принимать равным кварталу или полугодию, что избавляет от необходимости y1 рассмотрения специальных вопросов оперативно-календарного планирования.
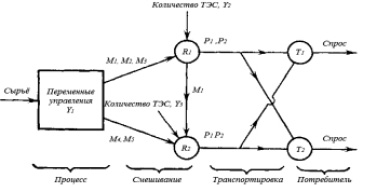
Рис. 1. Система производства и распределения лесопродукции
Рассмотрим теперь возможность использования нелинейной модели (1) для решения последней задачи. Пусть предприятия R1 и R2 производят продукты P1 и Р2 и отправляют их в пункты потребления T1 и Т2. Суммарный спрос (за весь период) на продукцию в этих пунктах предполагается известным и пусть D(Pi, Тj) – величина спроса на продукт Рi в пункте Тj. На предприятии R1 три вида лесоматериалов (сырья) М1, М2, М3 могут быть использованы для получения продуктов P1 и Р2. Кроме того, лесоматериал M1 может быть использован на предприятии R2 для смешения с лесоматериалами М4 и М5. Эту ситуацию схематически можно представить в виде схемы, представленной на рис. 1. Исходя из общей постановки задачи модель оптимального размещения выпуска однородной продукции с учётом минимизации совокупных затрат на производство и транспорт может быть записана в следующем виде:
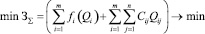 (2)
(2)
при ограничениях
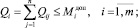 (3)
(3)
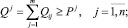 (4)
(4)
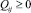 , (5)
, (5)
где i, j – индексы возможных пунктов производства и соответственно пунктов потребления продукции; 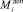 – объёмы производства и соответственно предельно допустимые их величины в i-м пункте; Qij – интенсивность транспортно-экономической связи между пунктами i и пунктами j; fi(Qi) – функция производственных затрат в i-м пункте; Cij – удельные транспортные затраты на перевозки между пунктами i и j; Pj, Qj – необходимый объём потребления и соответственно объём доставляемой в j-й пункт продукции.
– объёмы производства и соответственно предельно допустимые их величины в i-м пункте; Qij – интенсивность транспортно-экономической связи между пунктами i и пунктами j; fi(Qi) – функция производственных затрат в i-м пункте; Cij – удельные транспортные затраты на перевозки между пунктами i и j; Pj, Qj – необходимый объём потребления и соответственно объём доставляемой в j-й пункт продукции.
Из анализа модели (2)–(5) можно установить, что определяющее влияние на размещение производства оказывает не абсолютный уровень транспортных затрат, а дифференциация их по различным связям: чем меньше эта дифференциация, тем слабее влияние транспорта. При малых или относительно постоянных затратах оптимальный план определяется из условия минимума только производственных затрат.
На практике задача размещения и развития производства решается при следующих условиях.
1. Пункты и объёмы потребления рассматриваемой продукции фиксированы, критерий – минимум приведённых затрат на производство и транспортировку лесопродукции.
2. Оптимизация размещения производств выполняется по всему предполагаемому объёму выпуска лесопродукции (а не только по его приросту).
3. В экономико-математических моделях транспортные блоки имеют линейную структуру с постоянными коэффициентами целевой функции – значениями удельных показателей транспортных затрат, не зависящими от объёма перевозок.
4. Расчёты выполняются изолировано по отдельным вариантам без непрерывного обмена информацией, поэтому суммарные загрузки всех видов транспортных потоков лесопродукции ещё неизвестны.
Показатели транспортных затрат должны отражать лишь дополнительные составляющие объёмов и направлений перевозок лесопродукции.
При решении транспортных оптимизационных задач предполагается, что найденные транспортно-экономические связи на этом этапе и транспортные потоки будут осуществляться в реальных текущих грузопотоках. Возникает проблема модификации исходной информации и процедуры решения с целью снижения отрицательного влияния хозяйственного механизма при реализации решения. Здесь можно выделить три следующих этапа:
а) подготовка информации для решения задачи о размещении;
б) выбор решения по минимуму приведенных затрат;
в) реализация принятого решения (определение рациональных потоков сырья и готовой продукции по минимуму тарифных затрат).
Если тарифы совпадают с соответствующими дифференциальными удельными приведёнными транспортными затратами, то потери качества решения не происходит.
Таким образом, проблема учёта транспортного фактора в рассматриваемых задачах требует не только оптимизационного подхода на основе критериев экономической эффективности, но и учёта особенностей, которые вносит в реализацию оптимизационных планов специфика действующего производственного процесса.
Рассмотрим модель размещения пунктов потребления (хранения, переработки) лесопродукции и задачи функционирования лесопромышленных предприятий в разных условиях хозяйствования.
Все они преобразуются в блочно-диагональные линейные задачи, если зафиксировать значения некоторых переменных. Рассмотрим проблему в общем сетевом ракурсе.
Минимизировать
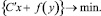 (6)
(6)
При ограничениях
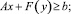 (7)
(7)
x ≥ 0, y ∈ S, (8)
где x – n-мерный вектор; А – постоянная диагональная матрица; C – n-мерный вектор констант.
Если зафиксировать значение у, то (1)–(3) переходят в задачу линейного программирования. Величина f(y) – функция (возможно нелинейная) р-мерного вектора у; F(y) – вектор-функция; S – произвольное подмножество Ep.
Многие важные в практическом отношении задачи могут быть приведены к виду (1)–(3). Если S′ – множество р-векторов с неотрицательными целочисленными компонентами, а F, f – линейны, то (1)–(3) окажется задачей линейного программирования.
В соответствии с этим алгоритм задачи (1)–(3) решают в следующей последовательности: вначале фиксируется некоторое значение y* ∈ S и решается задача: минимизировать C′x при ограничениях
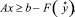 (9)
(9)
Затем на основе решения двойственной задачи декомпозиции определяется возможность улучшения решения, полученного на первом шаге и находится новое значение вектора у. Таким образом, полностью используются преимущества частичной линейной задачи, что особенно важно, когда матрица А имеет специальную структуру (например, блочно-диагональную или транспортного типа). В этом случае задача (4) сравнительно легко решается. Эти преимущества не реализуются при использовании алгоритмов, в которых х и у изменяются одновременно [1].
При формулировке задачи используются как дискретные, так и непрерывные переменные (дискретные – строить или не строить предприятие или склад, непрерывные соответствуют объёмам производства и поставок лесопродукции).
Функция текущих затрат, представленная на рис. 2, учитывает хорошо известный факт: с увеличением мощности предприятия возрастают условно-постоянные затраты, однако их увеличение компенсируется снижением условно-переменных затрат, что отражает преимущества крупных предприятий (то есть на таких предприятиях затраты на единицу продукции меньше, чем на мелких предприятиях). Сведение задачи размещения предприятий к задаче линейного программирования позволяет, как правило, сделать процедуру перебора вариантов более эффективной [2].
Введём обозначения: rj – спрос j-го потребителя; Cij – удельные транспортные затраты на перевозку единицы лесопродукции из пункта i потребителю j; xij – объём перевозок из пункта i в пункт j; mik – количество лесопродукции, привозимой (накапливаемой) предприятием i (складом i) при работе по k-му варианту (с затратами на прирост единицы продукта, равными Sik); Jp, Jw, Jc – множества номеров пунктов производства, складов и потребителей соответственно.
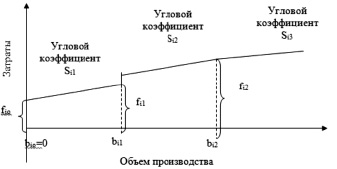
Рис. 2. Кусочно-линейная разрывная функция затрат
Переменные mik ограничены сверху и снизу и должны удовлетворять дополнительным условиям из-за наличия взаимоисключающих вариантов мощности k.
Чтобы учесть условия, введём переменные yik, принимающие значения нуль или единица (0 или 1), так что
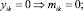 (10)
(10)
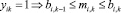 (11)
(11)
и не более чем одна переменная yik = 1 для каждого пункта производства i. Соответствующие ограничения можно представить в виде
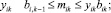 (12)
(12)
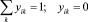 или 1.
или 1.
Так как спрос должен быть удовлетворен полностью, возникают ограничения
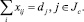 (13)
(13)
Переменные xij и mik связаны между собой ограничением
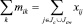 (14)
(14)
или вида
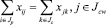 (15)
(15)
(то есть с каждого склада входящие и выходящие потоки лесопродукции равны между собой). Ёмкость склада ограничена, поэтому должно соблюдаться ограничение
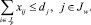 (16)
(16)
Общие затраты должны быть минимальными, то есть
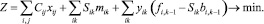 (17)
(17)
Первый член этого выражения – транспортные издержки, а второй и третий соответствуют затратам на строительство предприятия и производство продукции. Выражения (12)–(17) могут быть приведены к виду (6)–(8), в которых F и f – линейные функции, а S – множество возможных значений переменных yik. Выражения (12)–(17) решаются в два приёма: вначале фиксируются некоторые значения переменных yik, и решается линейная задача. Затем в результате решения целочисленной задачи определяются новые значения yik.
Выводы
Оптимальные решения задачи, двойственной к линейной, используются для построения дополнительных ограничений в целочисленной задаче, что уменьшает множество допустимых альтернатив, проверяемых на оптимальность. Таким образом, эта процедура может быть рассмотрена как схема, «автоматизирующая» перебор вариантов, в которой информация о ранее рассмотренных случаях используется для выделения случаев, которые следует рассматривать далее.
Рецензенты:
Сушков С.И., д.т.н., профессор кафедры технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Павлов А.И., д.т.н., профессор кафедры лесных, деревообрабатывающих машин и материаловедения, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Работа поступила в редакцию 28.07.2014.



