Необходимым условием эффективной политики социально-экономического развития является правильная диагностика проблем и постановка задач, умение выбрать приоритеты. В качестве стратегических целей развития страны выдвигается повышение благосостояния населения на основе динамичного и устойчивого экономического роста [1].
Следует отметить, что повышение благосостояния населения (уровня жизни) не всегда можно связывать с ростом ВВП. Задача увеличения ВВП может быть реализована при условии эффективно работающих производственных фондов, имеющих отдачу, превышающую расходы на их обслуживание. В противном случае подобное увеличение приводит к падению уровня жизни населения.
Формирование стратегии развития, цель которой – повышение благосостояния населения, качества жизни на фоне устойчивого экономического роста, является управленческой задачей. Данная задача оптимального распределения ресурсов заключается в определении научно обоснованных объемов финансирования социальной и производственной сфер.
Во многих практических приложениях при построении стратегии оптимального управления экономическими системами используется одномерная макромодель экономической динамики, известная как модель Рамсея-Касса-Купманса (РКК-модель) [2-4]. Развитие РКК-модели представлено работами Макарова В.Л., Рубинова А.М., Беленького В.З., Матвеенко В.Д. [5-8].
В большинстве работ рассматриваются одномерные модели [9] либо, гораздо реже, двумерные [10]. Многомерные задачи в большинстве случаев решаются сведением к одномерным. Развитие математического аппарата для решения n-мерных задач дает возможность рассматривать более широкий спектр прикладных проблем.
При рассмотрении процесса производства однородного валового регионального продукта (ВРП) предусмотрим возможность учета произвольного числа факторов; 
– вектор факторов производства, причем 
. Объем выпуска определяется n-факторной производственной функцией 
. Каждый год происходит распределение произведенного продукта на 
часть: инвестиции в развитие 
факторов производства согласно вектору управления 
и потребление. В качестве критерия оптимальности выберем максимальное накопленное за весь период планирования потребление на душу населения. Будем различать население трудоспособного возраста 
, задействованное в создании ВРП, и все население региона 
, на которое распространяется потребление в экономической системе [11]. Тогда 
– доля трудоспособного населения в общей численности.
Введем в рассмотрение множество допустимых векторов управления 
:
.
Функции управления определим как линейные функции относительно переменных управления 
: 
, где 
– показатель степени эффективности инвестиций в 
-й фактор; 
– параметр, учитывающий возможность обеспечения минимальных ежепериодных вложений для фактора (если существует такая необходимость). Заметим, что 
.
Накопленное за 
лет среднедушевое потребление определим как интеграл вида
,
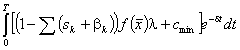где множитель 
– доля потребления в произведенном удельном (на одного работающего) ВРП за вычетом гарантированного минимального уровня потребления:
.
Тогда критериальный функционал задачи:
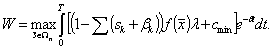
Фазовые уравнения системы, описывающие динамику факторов производства (фазовых координат), имеют вид:
,
где 
– составляющие вектора коэффициентов амортизации, согласно которым происходит выбытие факторов производства; 
и 
– начальные и конечные условия соответственно.
Для построения оптимальной стратегии воспользуемся принципом максимума Понтрягина [12]. В результате решения определим координаты квазистационарной траектории 
и реализующее ее оптимальное управление 
. Решение задачи показало, что в общем случае движение макроэкономической системы состоит из трех этапов: этап выравнивания уровней значимости факторов, выход на квазистационарную траекторию и движение по ней.
Таким образом, предложена многофакторная макроэкономическая модель, предназначенная для проведения прогнозных научно-аналитических расчетов развития экономики, позволяющая проводить расчеты траектории развития региона при различных вариантах социально-экономической политики.
СПИСОК ЛИТЕРАТУРЫ:
- Послание Федеральному Собранию Российской Федерации, 10 мая 2006 года // Официальный сайт Президента России htpp://www.kremlin.ru/text/appears/2006/05/105546.shtml
- Ramsey F.P. A mathematical theory of saving. Econ. Journ., December 1928. - с.543-559.
- Koopmans T.C. On the concept of optimal economic growth. Ex Aedibvs Academicis in Civitate Vaticana, 1965. – с.225-287.
- Cass D. Optimum saving in an Aggregative Model of Capital Accumulation, - 1963.
- Макаров В.Л., Рубинов А.М. Математическая теория экономической динамики и равновесия. – М.: Наука, 1973.
- Беленький В.З. Стационарные модели экономической динамики. – М.: ЦЭМИ РАН, 1981.
- Беленький В.З. Оптимальное управление: принцип максимума и динамическое программирование. М., ЦЭМИ РАН - РЭШ, 2001.
- Матвеенко В.Д. Эффективный функционал и магистраль в моделях экономической динамики // В сб. “Математические модели экономической динамики”, Вильнюс: ИЭ АН Лит.ССР, 1988.
- Беленький В.З., Кетова К.В. Полное аналитическое решение макромодели развития региона при экзогенном демографическом прогнозе. ЭММ, 2006, вып. 4.
- Кетова К.В., Сабирова О.Р. Макромодель развития региона с учетом повышения качества трудовых ресурсов // Анализ и моделирование экономических процессов / Сборник статей под ред. В.З.Беленького. Выпуск 3 -М.: ЦЭМИ РАН, 2006.-С. 83-98.
- Русяк И.Г., Кетова К.В. Анализ решения задачи управления демоэкономическим состоянием региона // В сб. Интеллектуальные системы в производстве.– Москва (МГУ)-Ижевск (ИжГТУ): Изд-во ИжГТУ, 2003.– №2.– С. 151-160.
- Понтрягин Л.С. Принцип максимума в оптимальном управлении. – М.: Наука, 1989.