Электромембранные системы широко используются для обессоливания растворов, для извлечения определенных типов ионов, для создания микро- и нанокинетических устройств [1]. Для повышения эффективности этих процессов и устройств используются математические модели. В настоящее время для математического моделирования процессов переноса в электромембранных системах используется система уравнений Нернста ‒ Планка и Пуассона [2]. Однако эта система уравнений неудобна для численного и асимптотического решения. В работах [3, 4] нами была предложена новая математическая модель переноса тернарного электролита на основе разработанного нами метода декомпозиции системы уравнений Нернста ‒ Планка и Пуассона и обоснована ее адекватность. В данной статье предлагается асимптотическое решение двумерной краевой задачи, соответствующей модели переноса тернарного электролита в приближении обобщенного закона Ома. Основная идея решения заключается в разбиении области решения, например канала обессоливания электродиализного аппарата, на несколько областей: область электронейтральности, область пространственного заряда, промежуточная область. Особенностью предлагаемого асимптотического метода является то, что в области пространственного заряда для однозначной разрешимости уравнений для текущего приближения необходимо использовать условие разрешимости уравнений для следующего приближения. Границы областей электронейтральности и пространственного заряда определяются по ходу решения. Однако для канала обессоливания можно указать, что область электронейтральности расположена в ядре потока, а область пространственного слоя примыкает к границам ионообменная мембрана/раствор (рисунок).
Постановка задачи
Система декомпозиционных уравнений в приближении закона Ома тернарного электролита имеет безразмерный вид [5]:
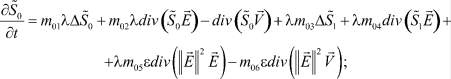 (1)
(1)
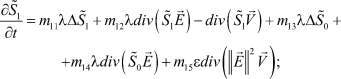 (2)
(2)
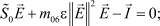 (3)
(3)
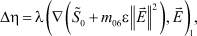 (4)
(4)
где 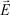 – искомая напряженность;
– искомая напряженность; 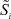 – обобщенные суммарные концентрации ионов;
– обобщенные суммарные концентрации ионов; 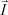 – плотность тока; η – функция тока для плотности тока
– плотность тока; η – функция тока для плотности тока 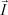 , т.е. I1 = –ηy, I2 = –ηx; ε > 0 – безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала; λ = 1/Pe, Pe – число Пекле;
, т.е. I1 = –ηy, I2 = –ηx; ε > 0 – безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала; λ = 1/Pe, Pe – число Пекле; 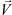 – заданная скорость протока электролита в камере обессоливания; L – длина канала, m i,j – некоторые постоянные зависящие от зарядовых чисел ионов zi и коэффициентов диффузии ионов Di,
– заданная скорость протока электролита в камере обессоливания; L – длина канала, m i,j – некоторые постоянные зависящие от зарядовых чисел ионов zi и коэффициентов диффузии ионов Di, 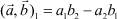 – кососимметрическое скалярное произведение.
– кососимметрическое скалярное произведение.
Для рассматриваемой системы уравнений (1)–(4) можно поставить различные краевые условия в зависимости от цели конкретного исследования. Мы здесь ограничимся формальным асимптотическим решением без конкретизации краевых условий.
Асимптотическое решение в области электронейтральности
Асимптотическое разложение
Для нахождения решения в области U2 используем разложение:
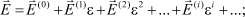
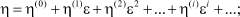
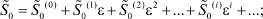
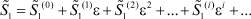
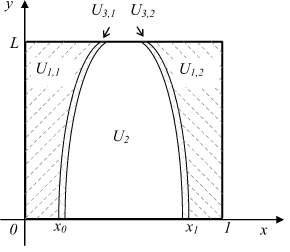
Схема разбиения области решения 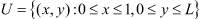 на подобласти по знаку функции
на подобласти по знаку функции 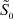 :
: 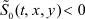 , при
, при 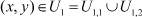 для любого t ≥ 0 (область пространственного заряда, примыкающая к ионообменным мембранам);
для любого t ≥ 0 (область пространственного заряда, примыкающая к ионообменным мембранам); 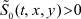 , при (x, y) ∈ U2 (область электронейтральности, расположенная в ядре потока);
, при (x, y) ∈ U2 (область электронейтральности, расположенная в ядре потока); 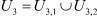 – промежуточный слой (
– промежуточный слой (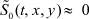 ). Здесь x = 0 – соответствует анионообменной, x = 1,– катионообменной x = 1 мембранам, y = 0, – входу, а y = L ‒ выходу из канала обессоливания
). Здесь x = 0 – соответствует анионообменной, x = 1,– катионообменной x = 1 мембранам, y = 0, – входу, а y = L ‒ выходу из канала обессоливания
Ниже приведены уравнения для начального приближения и показан алгоритм их решения. Уравнения произвольного приближения выписываются и решаются аналогично и здесь не приводятся из-за их громоздкости.
Алгоритм решения начального приближения
Для начального приближения получается следующая система уравнений:
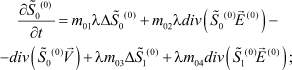 (5)
(5)
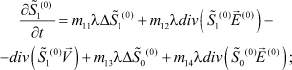 (6)
(6)
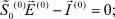 (7)
(7)
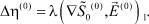 (8)
(8)
После ряда преобразований получаем систему уравнений для начального приближения:
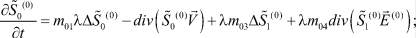 (9)
(9)
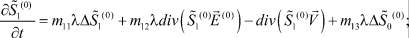 (10)
(10)
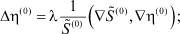 (11)
(11)
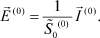 (12)
(12)
Заметим, что (9)–(12) является системой нестационарных квазилинейных уравнений второго порядка в каноническом виде и поэтому их исследование и решения возможны с использованием стандартных методов математической физики.
Асимптотическое решение в области пространственного заряда
Асимптотическое разложение
Для удобства асимптотического разложения в системе декомпозиционных уравнений (1)–(4) сделаем замену 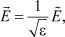 , тогда система примет вид
, тогда система примет вид
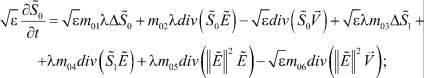 (13)
(13)
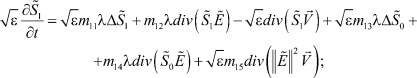 (14)
(14)
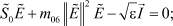 (15)
(15)
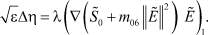 (16)
(16)
Для асимптотического решения используем разложения искомых функций в ряд по дробным степеням малого параметра ε:
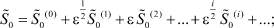 (17)
(17)
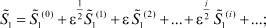 (18)
(18)
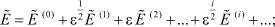 (19)
(19)
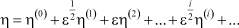 (20)
(20)
Ниже будет показано, что для нахождения начального приближения необходимо использовать уравнения для следующего приближения, поэтому необходимо записать системы уравнений для первых двух приближений.
Алгоритм решения начального приближения
Система уравнений, полученная подстановкой (17)–(20) в (13)–(16) и приравниванием слагаемых, не содержащих малого параметра, имеет вид
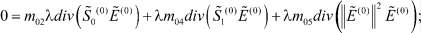 (21)
(21)
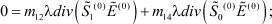 (22)
(22)
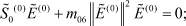 (23)
(23)
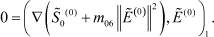 (24)
(24)
Ниже будет показано, что этой системы уравнений недостаточно для нахождения начального приближения. Для этого потребуется еще система уравнений приравниванием слагаемых при 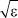 , которая имеет вид
, которая имеет вид
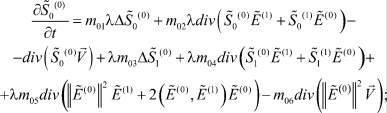 (25)
(25)
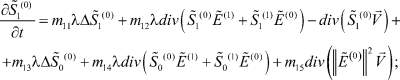 (26)
(26)
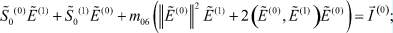 (27)
(27)
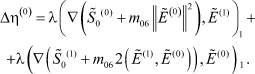 (28)
(28)
1. Рассмотрим уравнения (21), (22) для функций 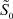 и
и 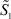 :
:
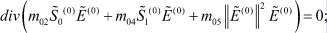
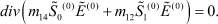
Из этих уравнений, после ряда преобразований с учетом 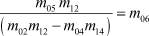 , получаем:
, получаем:
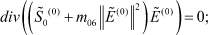
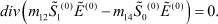 (29)
(29)
С учетом уравнения (23) первое уравнение является тождеством.
Следовательно, система уравнений (21)–(24) не позволяет однозначно найти решение для начального приближения системы.
Из уравнения (23) для функции 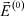 получаем уравнение, имеющее физический смысл:
получаем уравнение, имеющее физический смысл:
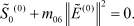 (30)
(30)
Уравнение (30) не позволяет однозначно определить нулевое приближение для функции 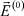 , поэтому необходимо еще одно скалярное уравнение, которое получается из условия разрешимости следующего приближения.
, поэтому необходимо еще одно скалярное уравнение, которое получается из условия разрешимости следующего приближения.
Из уравнения (27) для функции 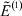 с учетом уравнения (23) имеем
с учетом уравнения (23) имеем
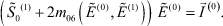 (31)
(31)
Это уравнение можно записать в виде
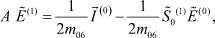 (32)
(32)
где 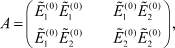 причем det A = 0.
причем det A = 0.
Условие разрешимости (32) имеет вид
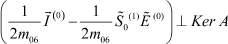
или, с учетом 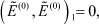 , получаем следующее условие разрешимости:
, получаем следующее условие разрешимости:
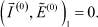 (33)
(33)
Итак, для 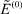 имеем систему, состоящую из уравнений (30) и (33), откуда
имеем систему, состоящую из уравнений (30) и (33), откуда
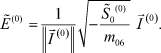 (34)
(34)
Из уравнения (28) для функции η(0) с учетом (23), имеем
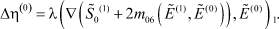 (35)
(35)
В правой части этого уравнения избавляемся от функций 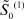 и
и 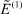 и получаем
и получаем
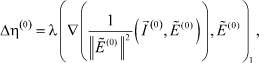 (36)
(36)
или с учетом (34), имеем
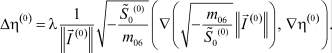 (37)
(37)
Рассмотрим уравнения (25), (26) и выведем из них еще одно уравнение для функций 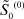 и
и 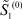 . В уравнении (26) избавимся от слагаемого
. В уравнении (26) избавимся от слагаемого 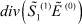 . После ряда преобразований получим
. После ряда преобразований получим
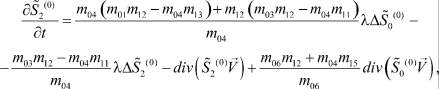
где 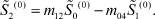 (38)
(38)
Уравнение (25) для функции 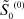 с учетом (46) запишется в виде
с учетом (46) запишется в виде
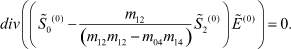 (39)
(39)
Таким образом, для нахождения начального приближения имеем следующую систему уравнений:
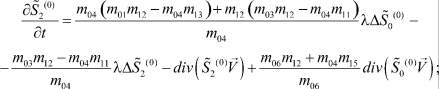
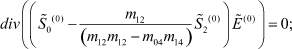
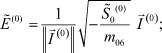
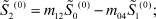
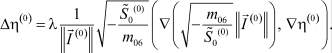
Промежуточные слои
Из асимптотических решений, приведенных выше, следует, что они не могут быть справедливыми в некоторой области (промежуточном слое), где 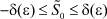 , причем δ(ε) → 0 при ε → 0. Для построения асимптотического разложения в этой области воспользуемся малостью функции
, причем δ(ε) → 0 при ε → 0. Для построения асимптотического разложения в этой области воспользуемся малостью функции 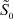 , тогда для нулевого приближения получим систему уравнений
, тогда для нулевого приближения получим систему уравнений
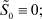
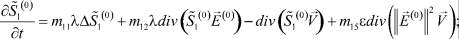 (40)
(40)
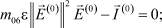 (41)
(41)
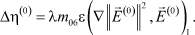 (42)
(42)
Систему уравнений после ряда преобразований можно привести к виду
 (43)
(43)
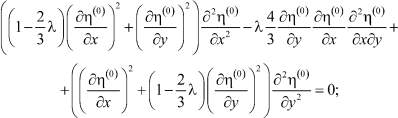 (44)
(44)
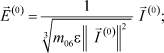 (45)
(45)
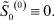 (46)
(46)
Из условия сращивания решений из области электронейтральности и промежуточного слоя, а также из области пространственного заряда и промежуточного слоя следует, что
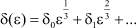 ,
,
где δ0, δ1, ... произвольные постоянные.
Заключение
Основная идея асимптотического решения заключается в разбиении области решения на несколько областей: область электронейтральности, область пространственного заряда, промежуточная область, границы которых определяются по ходу решения [5]. Особенностью предлагаемого асимптотического метода является то, что в области пространственного заряда для однозначной разрешимости уравнений для текущего приближения необходимо использовать условие разрешимости уравнений для следующего приближения.
Предложенное выше асимптотическое решение, в отличие от метода численного решения, позволяет находить решение при произвольно малых значениях параметра ε. Уравнения для коэффициентов разложения являются стандартными уравнениями математической физики, что упрощает их исследование, приближенное аналитическое и численное решения. Кроме того, формулы (12) и (34) дают аналитическое соотношение между плотностью тока и напряженностью электрического поля в областях электронейтральности и пространственного заряда.
Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов № 13-08-93106-НЦНИЛ_а, 13-08-93105-НЦНИЛ_а и № 13-08-00464 А.
Рецензенты:
Семенчин Е.А., д.ф.-м.н., профессор, заведующий кафедрой математических и компьютерных методов, Кубанский государственный университет, г. Краснодар;
Лебедев К.А., д.ф.-м.н., доцент, профессор кафедры вычислительной математики и математики, Кубанский государственный университет, г. Краснодар;
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения г. Хабаровск, профессор Университета Kwangwoon University, Korea.
Работа поступила в редакцию 28.05.2014.



