Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Обычно в литературе, например в [6], утверждается, что теплоёмкость жидкости близка к 3R, как у твёрдых тел. Однако таблицы теплоёмкости C_p, приведенные в [2], показывают, что эта теплоёмкость далека от 3R (в связи с малой расширяемостью жидкости C_v ≈ C_p). Так, теплоёмкость жидкого аргона при давлении 20 бар и температуре 85°К равна 4,7R, а при Т = 120°К – 6,32R, а при давлении 40 бар и Т = 145°К теплоёмкость С_р достигает значения 11,45R. Оказалось, что теплоёмкость жидкости зависит как от Т, так и от Р. При повышении температуры при том же давлении Р теплоёмкость увеличивается, а при повышении давления при Т = const она уменьшается.

На мой взгляд, изменение теплоёмкости связано с изменением числа ближайших соседей, т.е. координационного числа. В статье [5] была получена формула теплоёмкости С_v с учетом изменения координационного числа. Изменение этого числа при изменении температуры, т.е. df/dT, подсчитывалось с использованием идеи Я.И. Френкеля о разбиении жидкости на Z областей, каждая из которых содержит f частиц. Подсчитав увеличение энтропии и свободной энергии, там была получена следующая формула для f:

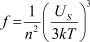, (1)

где U_S – энергия единицы поверхности; n – число частиц в единице объёма. Однако полученная из (1) формула для df/dT давала завышенные результаты. В данной статье сделана попытка найти df/dT с учетом другой связи U_S и f, а также зависимости U_S от σ и Т. Зависимость σ(Т), приведенная в [3] не дала желаемого результата. Поэтому использовалась формула σ(Т), взятая в [4].

Вывод формулы для С_v

В [7] приводится следующая формула для потенциальной энергии молекулы жидкости, окруженной f соседними молекулами:

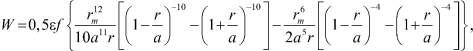(2)

где r_m – равновесное расстояние в потенциале Леннарда-Джонса; «a» – равновесное расстояние между молекулами в жидкости, ε – глубина потенциальной ямы в потенциале Леннарда-Джонса. Эта формула получена в результате усреднения потенциала взаимодействия частицы, находящейся в центре сферы, на которой находится f молекул, по всем направлениям колебания выбранной частицы. Если круглые скобки разложить в ряд по степеням 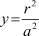, то, учитывая малость y, получим

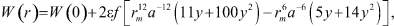(3)

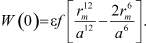где (4)

Выражение в квадратной скобке можно представить в ином виде:

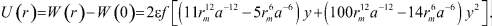(5)

Как известно, 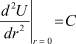 – есть коэффициент жёсткости молекулярных квазипружин:

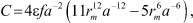(6)

с помощью которого определяется частота колебаний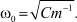

Хотя наличие слагаемого с r4 указывает на то, что колебания молекул нелинейные с частотой ω ≠ ω₀, тем не менее будем считать, что все молекулы колеблются с одинаковой частотой ω = ω₀, т.е. воспользуемся моделью А. Эйнштейна.

В этом случае свободная энергия, приходящаяся на одну частицу, имеет вид

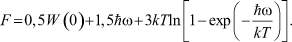(7)

Тогда, учитывая, что U = F + TS и 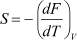, для внутренней энергии, приходящейся на одну частицу, получаем:

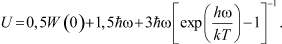(8)

Дифференцируя (8) по Т с учётом того, что W(0) зависит от координационного числа f, являющегося функцией температуры, получим:

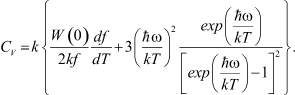(9)

В W(0) и С можно сделать замену: 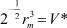 – собственный объём молекулы, a₃ = V₁ – объём, приходящийся на одну частицу. В этом случае

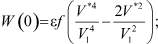(10)

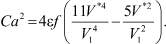(11)

Объём V₁ находится из таблиц, например [2] по удельному объёму:

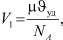(12)

где N_A – число Авогадро.

Зависимость координационного числа от температуры

В статье [5] для получения такой зависимости, как выше было сказано, использовалась идея Я.И. Френкеля, которая дала завышенное значение теплоёмкости. Здесь предлагается использовать зависимость коэффициента поверхностного натяжения от температуры. Будем исходить из того, что жидкость кластеризована и кластер представляет собой капельку жидкости. Если энергию одной частицы, находящейся на поверхности, обозначить через W, то энергия всей поверхности будет

U = WN_пов,

где N_пов – число поверхностных молекул. Энергия единицы поверхности равна

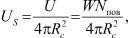
где R_c – радиус кластера. Пусть эффективный радиус молекулы (радиус Вигнера ‒ Зейтца) равен R₀. Тогда

R_c = R₀n ^2/3,

где n – число частиц в кластере.

Следовательно

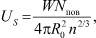
но 4n ^2/3 = N_пов. Поэтому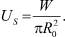

Энергия молекулы на поверхности и энергия молекулы, находящейся внутри кластера, связаны некоторым образом. Будем считать, что энергия поверхностной молекулы составляет часть α от энергии внутренней частицы. Тогда

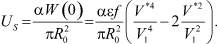
Дифференцируя это равенство по Т, нетрудно получить:

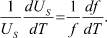(13)

Согласно [4]

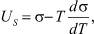(14)

а

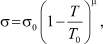(15)

где Т₀ – критическая температура; σ – коэффициент поверхностного натяжения; σ₀ и μ – константы, причем μ = 1,24.

Используя равенства (13)‒(15), можно определить df/dT. Так как

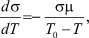
то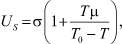

или

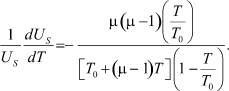(16)

Поскольку U_S пропорционально f, то это же выражение будет определять и df/dT:

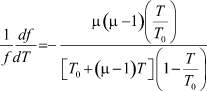
или, подставив μ = 1,24, можно записать

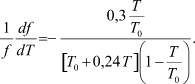(17)

После интегрирования получается следующее выражение для f:

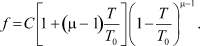(18)

Постоянную С можно определить, если известно f при какой-либо температуре. Согласно [1] координационное число у аргона равно 10,3. Хотя температура там не указана, будем считать Т = 85°К. Тогда получается С = 11,18 и при Т = 120°К f = 9,06, а при 140°К f = 7,15. При 85°К (17) оказалось равным 0,0023, т.е. величиной, существенно меньшей единицы. Это позволяет считать, что df/dT практически не сказывается на частоте колебаний.

Вычисление теплоёмкости CV с помощью (9) и (17)

Чтобы воспользоваться формулой (9), необходимо определить частоту колебаний, которая зависит от отношения 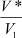и от координационного числа. Используя (12), найдем частоту колебаний:

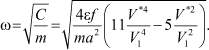
Обозначим диаметр молекулы буквой D. Тогда V* = D3, 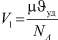и 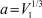. При 85°К и Р = 20 бар получаем: ω0 = 3,847∙1012; 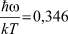; ; 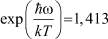f = 10,3. Тогда первое слагаемое в (9) равно 1,42, а второе слагаемое ‒ 2,975. Следовательно, теплоёмкость C_V = 4,39R.

Произведем эти же вычисления при Р = 20 бар и Т = 120°К. Первое слагаемое в (9) равно 2,64, а второе – 3,044. Таким образом, C_V = 5,68R.

Табличное значение C_P при этих температурах равно 4,7R и 6,3R соответственно. Таким образом, при 85°К погрешность вычислений составляет 6,5 %, а при 120°К – 9,8 %. Это в том случае, если C_V ≈ C_P. На самом деле C_V несколько меньше, чем С_Р и, следовательно, погрешность будет меньше. При Р = 40 бар и Т = 140°К наши вычисления дают C_V = 8,35R, а табличное значение C_V = 9R, т.е. погрешность равна 7,2 %.

Погрешность формулы, возможно, определяется неточностью вычисления координационного числа. Так, если при 85°К считать число соседних молекул равным 12, то постоянная С в (18) будет иметь значение 12,9 и координационное число при Т = 120°К и Т = 140°К увеличивается до 10,47 и 8,25 соответственно. Погрешность формулы (9) при этом сокращается. Поэтому определение координационного числа в жидкости и его зависимости от температуры остаётся актуальной задачей. Кроме этого, уменьшить погрешность можно, подбирая число μ.

Выводы

1. Вклад колебательного движения молекул жидкости в теплоёмкость составляет 3R, если частота колебаний не зависит от температуры.
2. Существенный вклад в теплоёмкость жидкостей даёт потенциальная энергия взаимодействия молекул. При низких температурах он составляет более 1,5R, а при высоких температурах – от 3R до 6R и более.
3. Разработанный способ подсчёта зависимости координационного числа от температуры даёт удовлетворительные результаты. Погрешность подсчёта теплоёмкости с помощью рассчитанных значений f и df/dT не превышает 10 %.

Рецензенты:

Плотников С.В., д.ф.-м.н., профессор, заведующий кафедрой «Техническая физика», Восточно-Казахстанский государственный технический университет им. Д. Серикбаева, г. Усть-Каменогорск;

Алонцева Д.Л., д.ф.-м.н., профессор кафедры «Программирование и автоматизация технологических процессов», Восточно-Казахстанский государственный технический университет им. Д. Серикбаева, г. Усть-Каменогорск;

Бичурин М.И., д.ф.-м.н., профессор, зав. кафедрой «Проектирование и технология радиоаппаратуры», Новгородский государственный университет, г. Великий Новгород.

Работа поступила в редакцию 30.04.2014.