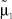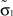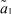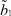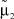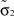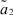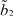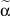Восстановление функции распределения по выборке случайных данных, полученных в результате проведения тех или иных экспериментов, является основной задачей математической статистики [1], которая имеет важное практическое значение, например, при решении задач прочностной надежности элементов и объектов нефтегазового оборудования [2]. Обсуждаемая задача имеет следующую постановку: по экспериментальной выборке значений случайной величины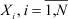 
из генеральной совокупности найти функцию распределения F(y) = Pr{X ≤ y}, связанную с плотностью распределения f(y) интегральным отношением:
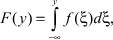. (1)
Известны два основных подхода к решению этой задачи: параметрический и непараметрический.
Параметрический подход предусматривает выбор на основе той априорной информации вида функции распределения случайной величины F(y), зависящей от некоторого набора параметров, и получении оценок их значений по имеющейся выборке данных, обеспечивающих максимальную близость теоретической функции распределения F(y) и эмпирической функции распределения
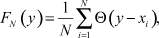(2)
где функция Хэвисайда
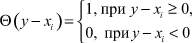
в соответствии с выбранной мерой близости, зависящей, вообще говоря, от вида распределения [3].
Существование решения обсуждаемой задачи обеспечивает центральная теорема математической статистики, согласно которой с ростом объема выборки N функция FN(y) с вероятностью, равной единице, равномерно приближается к F(y):
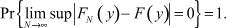
В основе непараметрической статистики лежит подход, позволяющий получать адаптивные оценки эмпирических распределений в виде некоторых функционалов, не зависящих от вида неизвестного априорного распределения [4]. Для восстановления неизвестной функции распределения в непараметрической статистике известен ряд методов и алгоритмов [4]: метод гистограмм, «гребенка», метод ближайших соседей, метод разложения по базисным функциям, аппроксимация Розенблатта – Парзена и ряд других. Работоспособность методов непараметрической статистики и целесообразность их применения при анализе экспериментальных данных подтверждается результатами, полученными различными исследователями (см. список литературы к разделу «Введение» в [4]). Например, в [2] показано, что аппроксимация Розенблатта – Парзена оказывается весьма эффективной в задаче оценки долговечности нефте- и газопроводов на основе анализа накопленной статистической информации.
Результаты исследования особенностей аппроксимации Розенблатта – Парзена в задаче аппроксимации одномодальных распределений дискретных и непрерывных случайных величин с ограниченной областью изложены в [5, 6] соответственно.
В связи с тем, что на практике, например при оценке прочностной надежности изделий [2] или анализе суточной выработки экскаваторов на горных работах [3], требуется получение оценок распределений случайных величин с двумодальными законами распределения, разработка методов оценки их параметров является актуальной задачей.
В данной статье приведено описание и обоснование методики оценки параметров двумодального распределения случайной величины, каждая мода которого имеет нормальный закон распределения с ограниченной областью рассеяния.
Функция изучаемого распределения записывается в следующем виде:
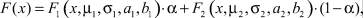(3)
где μ1 – математическое ожидание первой составляющей; σ1 – математическое ожидание первой составляющей; a1, b1 – границы области рассеяния первой составляющей; μ2 – математическое ожидание первой составляющей; σ2 – математическое ожидание первой составляющей; a2, b2 – границы области рассеяния первой составляющей; α – доля первой составляющей в общем распределении.
Пример двумодальной функции распределения случайной величины, каждая мода которого имеет нормальный закон распределения с ограниченной областью рассеяния, представлен на рис. 1.
Отметим, что в общем случае задача оценки параметров распределения сводится к решению той или иной системы нелинейных уравнений, для которых в подавляющем большинстве случаев приходится использовать соответствующие численные методы, например, итерационный метод Ньютона. Однако сходимость интеграционной последовательности к истинному решению оказывается очень сильно зависящей от выбора начального приближения. Вследствие этого в рассматриваемой задаче представляется перспективным использовать эвристические методы случайного поиска, результативность которых, как утверждается, не зависит от начального приближения и позволяет найти оптимальное решение при любых начальных условиях. Одним из таких методов являются генетические алгоритмы (ГА) [7], которые были использованы в проведенном исследовании.
На первом этапе исследования была изучена возможность одновременного получения оценок всех значений параметров двумодального распределения μ1, σ1, a1, b1, μ2, σ2, a2, b2, α с помощью ГА, в котором в качестве целевой функции использовались среднеквадратические отклонения отсортированной по возрастанию исходной последовательности и отсортированной по возрастанию последовательности, сгенерированной в соответствии с экспериментальным законом распределения (3):
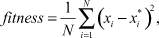(4)
где N – число элементов в исходной выборке; x – исходная выборка; x* – выборка, сгенерированная с помощью метода обратного преобразования в соответствии с законом (3) и текущими значениями параметров распределения, задаваемых ГА.
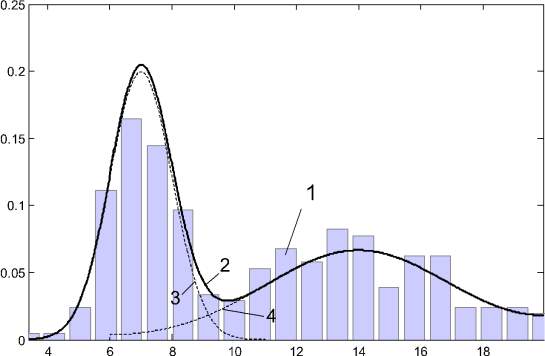
Рис. 1. Пример двумодального распределения: 1 – гистограмма случайной последовательности; 2 – плотность распределения случайной величины; 3 – график функции dF1(x, μ1, σ1, a1, b1)/dx; 4 – график функции dF2(x, μ2, σ2, a2, b2)/dx
Методика оценивания параметров двумодального распределения
Результаты многочисленных вычислительных экспериментов, проведенных при различных настройках ГА, показали, что получаемые значения были далеки от истинных – средняя погрешность вычислений составила боле 50 %. Этот результат, с нашей точки зрения, объясняется высокой размерностью пространства, в котором ищется минимум функции (7). Таким образом, прямое решение данной задачи с помощью ГА не является приемлемым. В этой связи возникла необходимость разработки методики решения рассматриваемой задачи, позволяющей уменьшить размерность пространства, в котором ищется минимум функции (4), за счет оценки одного или нескольких параметров, не используя ГА.
Для реализации данной идеи было предложено использовать метод Розенблатта ‒ Парзена, позволяющий аппроксимировать функции плотности распределения [8, 9, 6]. Результаты применения метода Розенблатта – Парзена к случайной последовательности с двумодальным распределением представлен на рис. 2.
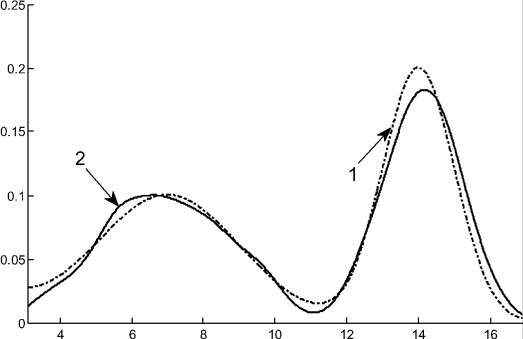
Рис. 2. Плотность двумодального распределения: 1 – теоретическая плотность двумодального распределения; 2 – аппроксимация Розенблатта – Парзена плотности распределения случайной последовательности, сгенерированной в соответствии с теоретическим законом распределения
Из рис. 2 видно, что на основе анализа аппроксимирующей кривой можно получать оценки математических ожиданий каждой из мод исходного распределения μ1,2, а также левую границу первой составляющей a1 и правую границу второй составляющей b2. Таким образом, с помощью ГА остается вычислить следующие параметры распределения σ1, b1, σ2, a2, α, т.е. удается уменьшить размерность задачи с 9 до 5.
Таким образом, методика нахождения параметров двумодального распределения случайной последовательности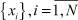 
(3) реализуется выполнением следующей последовательности действий:
1. Вычисление в соответствии с методом Розенблатта – Парзена значений функции, аппроксимирующей плотность распределения (3), – FRP(x).
2. Вычисление оценок значений параметров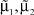 
– абсцисс локальных максимумов функции FRP(x).
3. Вычисление оценки левой границы области рассеяния моды распределения (3), описываемой функцией
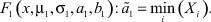
4. Вычисление оценки правой границы области рассеяния моды распределения (3), описываемой функцией
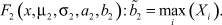
5. Вычислить, используя ГА, значения параметров σ1, b1, σ2, a2, α.
В ходе проведенных исследований мы использовали следующие настройки ГА:
- селекция: S = <равномерная; турнирная; на основе рулетки>;
- мутация: M = <адаптивная>, т.к. в задаче присутствуют ограничения;
- кроссовер: C = <одноточечный; двухточечный; усредненный; разбросанный, эвристический>;
- доля кроссовера: Cfr = <0,3; 0,6; 0,9> (оставшаяся часть приходилась на мутацию);
- размер популяции: P = <5, 15, 30>.
Таким образом, каждому из проведенных экспериментов можно поставить в соответствие определенный набор настроек – кортеж ⟨SS, Mm, CC, Cfrf, PPñ. Всего в проведенных экспериментах было рассмотрено
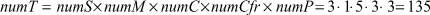
различных комбинаций настроек. Для каждого набора настроек было выполнено 50 независимых испытаний. Для повышения достоверности в качестве значений параметров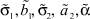 
принимались средние по ансамблю испытаний значения.
Для количественной оценки качества найденных значений параметров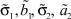 
решения мы использовали величину Δx:
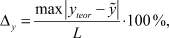(5)
где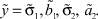 
Для количественной оценки качества найденного значения параметра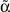 
мы использовали величину Δα:
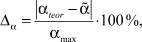(6)
где αmax = 1.
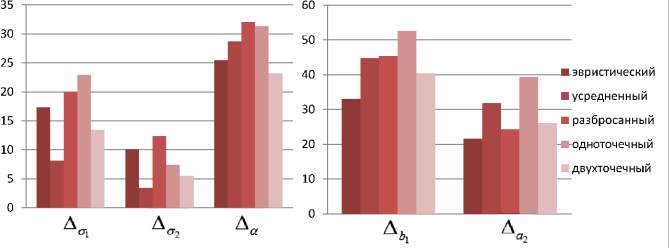
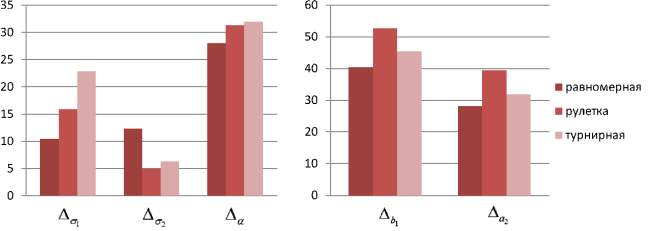
Результаты расчетов погрешностей параметров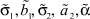 
в соответствии с (5), (6) для тестовых последовательностей, генерируемых в соответствии с (3), где μ1 = 7, σ1 = 2, a1 = 3, b1 = 14, μ2 = 714, σ2 = 1, a2 = 6, b2 = 18, α = 0,5, представлены на рис. 3.
Из рис. 3 видно, что виды селекции и кроссовера не оказывают существенного влияния на погрешность вычисления параметров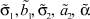 
. В то время как при увеличении доли кроссовера и числа особей в популяции точность вычисления ключевых параметров σ1, σ2, α увеличивается при одновременном увеличении времени расчетов. Приведем средние значения погрешностей параметров:
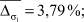
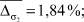
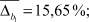
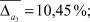
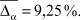
Для интегрального оценивания качества предложенной методики был использован следующий показатель:
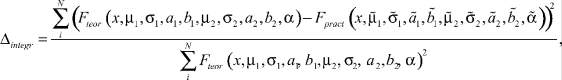
значения которого в проведенных вычислительных экспериментах изменялись в диапазоне
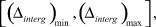
где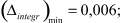 
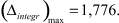Наилучший результат 
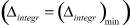получен при следующих настройках ГА:
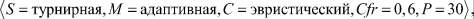
наихудший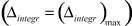 
‒
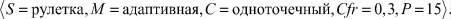
б
г
Рис. 3. а – погрешности в разрезе вида селекции – равномерной, на основе рулетки и турнирной селекции; б – погрешности в разрезе вида кроссовера – эвристический, усредненный, разбросанный, одноточечный и двухточечный; в – погрешности в разрезе доли кроссовера – 0,3; 0,6 и 0,9; г – погрешности в разрезе размера популяции – 5, 15 и 30 особей
Соответствующие параметры распределений представлены в таблице.
Теоретическая и экспериментальная плотности распределения представлены на рис. 4.
Наилучший и наихудший интегральные показатели
|
Параметры |
|
|
|
|
|
|
|
|
|
Δintegr |
|
Теоретические значения |
7 |
2 |
3 |
14 |
14 |
1 |
6 |
18 |
0,5 |
− |
|
Наихудший результат |
7,225 |
1,869 |
3,023 |
6,109 |
14,014 |
0,956 |
9,014 |
17,977 |
0,813 |
1,776 |
|
Наилучший результат |
7,225 |
2,113 |
3,023 |
15,203 |
14,014 |
1,051 |
5,269 |
17,977 |
0,474 |
0,006 |
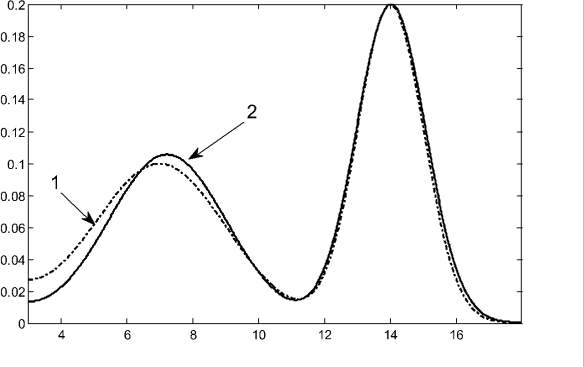
Рис. 4. 1 – Теоретическая и экспериментальная 
плотности: теоретическая плотность распределения; 2 – экспериментальная плотность распределения
Таким образом, полученные результаты позволяют сделать вывод о том, что предложенная методика в целом обеспечивает вполне приемлемый результат и ее можно использовать для оценивания параметров двумодальных распределений вида (3).
Выводы
Анализ результатов совместного применения аппроксимации Розенблатта – Парзена, метода мнимых источников и генетических алгоритмов в задаче оценивания значений параметров распределений случайных последовательностей двумодальными законами распределения вида (3), относящегося к классу 9-ти параметрических распределений, позволяет сделать следующие выводы:
- При использовании генетических алгоритмов для нахождения одновременно всех параметров изучаемого распределения погрешности оценок превышают 50 %, что является следствием высокой размерности решаемой задачи.
- Предложена методика нахождения параметров изучаемого двумодального распределения случайных последовательностей, основанная на совместном использовании аппроксимации Розенблатта – Парзена и ГА, и получено подтверждение ее работоспособности.
- Получены оценки точности нахождения параметров распределения, а также интегрального показателя, характеризующего в целом качество оценки плотности распределения случайной последовательности с изученным законом распределения.
Рецензенты:
Кубланов В.С., д.т.н., доцент, профессор кафедры радиоэлектроники информационных систем, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой информационных технологий, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 28.05.2014.