Любая радиоэлектронная система (РЭС) характеризуется набором случайных значений выходных параметров Yi (i = 1, k), которые отражают степень соответствия системы заданным техническим характеристикам. Система считается работоспособной, если эти параметры лежат в заданных пределах, т.е.
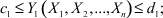
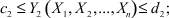
………………………………
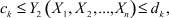
где Xj (j = 1, n) – параметры элементов системы, входных сигналов, внешних мешающих факторов, ci и di – верхняя и нижняя граница допустимых значений параметров системы. Контроль большого числа параметров требует значительных затрат, которые могут составлять от 30 до 40 % расходов на разработку и производство РЭС [6]. Поэтому актуальной является задача минимизировать данные расходы за счет повышения эффективности моделирования РЭС.
Моделирование является важнейшим этапом процесса разработки современных РЭС. Оно включает в себя определенный набор работ и этапов, который может существенно различаться для конкретных классов РЭС, что обусловлено их спецификой. Типичными этапами моделирования РЭС являются анализ технического задания, моделирование электрических схем и процессов в них, исследование разбросов и надежности, анализ результатов моделирования и т.д.
Несмотря на определенные различия, методология моделирования РЭС включает ряд базовых принципов, к которым относятся декомпозиция и иерархичность описаний, многоэтапность и итерационность моделирования, типизация и унификация полученных решений. Это, в свою очередь, позволяет говорить о целесообразности применения интеллектуальных систем моделирования сложных РЭС, опирающихся на анализ структурированных баз данных (БД) с целью ограничения круга сущностей, рассматриваемых при моделировании, и таким образом сократить перебор при выборе решения. Наиболее перспективным является применение интеллектуальных методов моделирования на таких этапах, как структурный синтез РЭС, особенно на ранних стадиях проектирования, а также расчет и анализ параметров объекта проектирования в различных режимах с учетом разброса параметров компонентов и наличия дестабилизирующих факторов.
Применение современных подходов для обработки БД, полученных по результатам измерений сложных РЭС и комплексов, требует дальнейшего развития. При этом важно отметить, что число измерений только для одной системы, например фазированной антенной решетки, может превышать 10 миллионов.
Интеллектуальные методы в задачах моделирования сложных РЭС
На каждом этапе производства сложных РЭС, начиная от гибридных и монолитных интегральных схем и заканчивая комплексом в целом, выделяются ключевые контролируемые параметры, которые позволяют при оптимальном объеме измерений обеспечить полный цикл отработки, настройки и выпуска готового изделия, полностью соответствующего требованиям технического задания. При этом на каждом этапе используются автоматизируемые, тестируемые измерительные комплексы и аппаратура для испытания на воздействие дестабилизирующих факторов (температура, влага, радиация, вибрация, ударная нагрузка и т.п.). Число измерений при изготовлении РЭС может превышать 10–15 миллионов. Поэтому все рабочие места от субмодулей до РЭС должны быть обеспечены аппаратурой с автоматизированным режимом измерения и регистрации данных, на основе которых формируются БД, где содержатся скрытые зависимости и закономерности между параметрами, знание которых позволяет повысить эффективность моделирования и разработки РЭС.
Построение моделей сложных РЭС электродинамическими методами, методами теории цепей и др., особенно с учетом влияния дестабилизирующих факторов, вызывает значительные математические трудности, требует существенных временных и человеческих ресурсов. Кроме этого, анализируемые данные могут оказаться неполными и неточными. Поэтому актуальной задачей моделирования РЭС является поиск методов анализа результатов контрольных измерений на основе методов и моделей, особенно в условиях неполной и неточной информации, воздействия различного рода мешающих и трудно поддающихся учету факторов.
Одним из направлений решения данной проблемы является использование интеллектуальных методов моделирования на основе алгоритмов и моделей машинного обучения (МО). Как известно, интеллектуальные методы в большинстве случаев являются эвристическими, т.е. не являясь полностью математически обоснованными и точными, позволяют тем не менее получить приемлемый результат в большинстве практически значимых случаев [2]. При этом они обладают значительно меньшей трудоемкостью, высокой прозрачностью для исследователя и обеспечивают хорошие возможности для автоматизации исследований. Недостатками эвристических моделей являются относительно низкая точность и неоднозначность решений, сильная зависимость от исходных данных.
Тем не менее данные недостатки отчасти компенсируются возможностью получения решений даже в условиях неполных, неточных и противоречивых данных, когда более точные методы оказываются бесполезными. Это достигается за счет высокой обобщающей способности, приобретаемой эвристическими моделями на основе обучения с использованием большого числа наблюдений, полученных по результатам измерений.
Краткий обзор интеллектуальных методов, используемых в моделировании РЭС
Наиболее часто используемыми видами эвристических моделей, применяемых для анализа больших структурированных массивов данных, являются модели, основанные на машинном обучении, такие, как нейронные сети (НС), деревья решений, самоорганизующиеся карты признаков, ассоциативные модели и другие. Данные модели также известны как интеллектуальные, поскольку кроме чисто математического аспекта позволяют исследователю дополнять решение своим опытом и знаниями, что и обеспечивает возможность получения решений даже в очень плохо формализованных случаях. Интеллектуальные модели позволяют решать задачи численного предсказания, классификации, кластеризации и ассоциации.
Численное предсказание обеспечивает моделирование непрерывных зависимостей между параметрами сложных РЭС, например, выходной мощности от уровня согласования между устройствами системы, контролируемых параметров гибридных и монолитных схем (фазовращателей, аттенюаторов, переключателей, усилителей и др.), условий эксплуатации и т.д. Обычно данная задача решается с помощью нейронной сети.
Нейронные сети. Как известно, НС представляет собой совокупность простейших вычислительных элементов, называемых искусственными нейронами, каждый из которых выполняет операцию взвешенного суммирования своих входов с последующим нелинейным преобразованием полученной суммы. Построение нейросетевой модели состоит из двух этапов [3]:
- задание параметров модели – определение числа нейронов и межнейронных связей, вида нелинейного преобразователя (активационной функции);
- обучение модели – итерационная корректировка весов межнейронных связей на основе алгоритма обучения, где на каждой итерации модели предъявляется обучающий пример.
Каждый обучающий пример представляет собой строку БД в которой хранится набор значений входных и выходных параметров РЭС, зарегистрированных при одном измерении. Алгоритмы обучения НС обычно основаны на градиентных методах оптимизации (например, наискорейшего спуска). Обучение продолжается до тех пор, пока отклик модели на заданный входной вектор значений параметров не окажется достаточно близким (например, в среднеквадратическом смысле) к фактически наблюдаемому выходному значению. Поэтому данный метод известен как «обучение с учителем».
Преимущество нейросетевых моделей заключается в том, что исследователь, подбирая параметры модели и контролируя процесс обучения, добивается необходимого уровня её точности и обобщающей способности (возможности работать с искаженными и неполными данными). При этом может использоваться опыт, полученный ранее при решении аналогичных задач. Практическое использование нейросетевых моделей заключается в том, что, подав на ее вход вектора параметров, зафиксированных в новом измерении или для нового устройства, сеть автоматически рассчитывает соответствующее выходное значение.
Деревья решений. При решении задач анализа данных большой размерности в условиях неполных, неточных данных и плохой формализуемости целей, что характерно для моделирования сложных технических систем вообще и РЭС в частности, улучшить обобщающую способность и понимаемость модели специалистом можно за счет категоризации целевых переменных, т.е. формирования классов, логически отражающих проблематику задачи, например классы устройств по точности, надежности и т.д. Система классификации разрабатывается экспертами и должна быть сформирована до начала моделирования.
Для решения задач классификации из интеллектуальных моделей наиболее часто используются деревья решений [4] – структуры индуктивных решающих правил вида «если – то», состоящие из узлов, где содержатся правила, и листьев, где формируется класс объекта, распределенного в данный лист. При этом правила формируются на естественном языке, что позволяет исследователю использовать модель не только как классификатор, но и извлекать полезные знания из самой структуры модели – отслеживать правила, через которые «прошёл» объект по данной ветви дерева, прежде чем был распределен в лист, ассоциированный с определенным классом. Это выгодно отличает деревья решений от НС, в которых извлечение полезной информации (вербализация) из структуры модели (весов межнейронных связей, вида функции активации и т.д.) невозможно. Поэтому деревья решений обладают высокой объясняющей способностью, что очень важно при моделировании сложных систем на основе данных большой размерности.
Самоорганизующиеся карты признаков. В задачах моделирования технических систем на основе данных тестовых измерений, полученных в реальных условиях (в особенности при воздействии мешающих факторов), часто оказывается, что значения целевой переменной частично отсутствуют или измерены с недостаточной точностью. Возможны задачи, когда целевую переменную вообще указать невозможно (т.е. нельзя выбрать параметр системы, который по логике задачи можно рассматривать как выходной). Следствием этого является невозможность формирования классов или целевой переменной для моделей, использующих обучение с учителем, к которым относятся НС и деревья решений.
В этом случае для интеллектуального моделирования РЭС удобно использовать кластеризацию – разбиение всего набора наблюдений, каждое из которых представляет собой серию измерений параметров устройств или системы в целом на однородные группы, называемые кластерами. Группировка в кластеры осуществляется на основе меры (например Евклида) расстояния между векторами наблюдений в многомерном пространстве по принципу: различие между двумя наблюдениями внутри кластера всегда меньше, чем различие между двумя наблюдениями из разных кластеров. Поскольку в процессе кластеризации целевая переменная не используется, ее называют обучением без учителя.
Результатом кластеризации является формирование однородных групп тестовых испытаний или технических объектов с однородными свойствами и типичными особенностями (например, похожими искажениями сигнала, одинаковыми условиями проведения испытаний, ухудшением отношения сигнал-шум при воздействии помех и т.д.). Изучив свойства кластера и выполнив его содержательную интерпретацию, исследователь может делать суждения о качественном и количественном влиянии одних параметров системы на другие, условий, при которых они возникают, разрабатывать меры по исключению негативных факторов. Практическое использование кластерной модели заключается в предъявлении ей векторов новых объектов или наблюдений, которые она распределит в один из кластеров, свойства которого могут быть обобщены на этот объект.
Одним из наиболее мощных и эффективных методов кластеризации многомерных данных являются самоорганизующиеся карты признаков (карты Кохонена) [5]. Они представляют собой специальный тип НС (сети Кохонена), обучаемых на основе конкурентного обучения (алгоритм Кохонена). Структура кластеров представляется в виде набора карт, каждая из которых отображает распределение одного из параметров, а весь набор ‒ распределение всех параметров по структуре кластеров. Основная задача карты Кохонена – представление результатов кластеризации многомерных данных, которая позволяет производить эффективное исследование свойств кластеров и их содержательную интерпретацию.
Инструменты интеллектуального моделирования РЭС
Одно из главных преимуществ интеллектуальных методов моделирования РЭС заключается в том, что они не требуют использования дорогостоящих специализированных систем, а могут быть реализованы на основе достаточно распространенного класса программных средств, реализующих технологии машинного обучения и построения моделей на их основе. Данный класс ПО известен как аналитические платформы и изначально предназначен для реализации проектов интеллектуального анализа данных (Data Mining) – методологии обнаружения зависимостей и закономерностей в многомерных массивах данных с целью получения знаний, необходимых для поддержки принятия решений в различных предметных областях. Наиболее типичными приложениями интеллектуальных платформ являются бизнес-аналитика, управление производством, прогнозирование в экономике и финансовой сфере, а также в медицине, биологии, науке и технике.
В настоящее время интеллектуальные платформы [1] достаточно широко представлены на рынке как свободно распространяемые (Veka, Rapid Mainer и др.), так и коммерческие (SAS Enterprise Miner, SPSS Data Modeler). Кроме этого модули интеллектуального моделирования реализованы в большинстве современных пакетов компьютерной математики, таких как MatLab и Statistica.
В данной работе была использована аналитическая платформа «Deductor» российской компании BaseGroup Labs в конфигурации, представленной на рисунке. Результаты тестовых измерений поступают в специализированное хранилище данных (ХД) Deductor Warehouse, в котором была сформирована соответствующая структура метаданных. Преимуществом использования ХД в сравнении с обычными БД является автоматическая поддержка целостности и непротиворечивости данных, на основе которых производится интеллектуальное моделирование, а также принцип их хронологичности, неизменчивости и интегрируемости из различных типов и источников.
Модуль Deductor Studio представляет собой рабочее место аналитика, который управляет процессом моделирования на основе технического задания и запросов, предоставленных техническими специалистами, занятыми непосредственно в разработке и конструировании устройств. Аналитик разрабатывает сценарий обработки данных и реализует построение и верификацию моделей, а также вспомогательные операции – очистку и предобработку данных.
По результатам моделирования формируются технические отчеты регламентированных форм, которые используются техническими специалистами для принятия решений в процессе разработки, конструирования и технологии производства РЭС. Рабочим местом технических специалистов является модуль Deductor Wiewer, который позволяет управлять техническими отчетами. Преимуществом данной конфигурации является разделение функций аналитика и инженерных работников, что позволяет сосредоточиться каждой из этих категорий на решении своего блока задач.
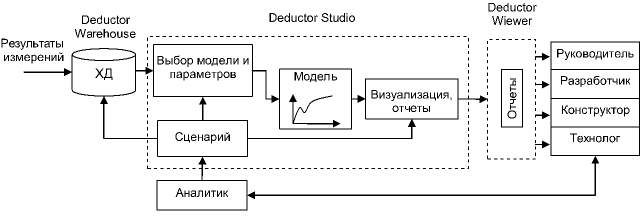
Конфигурация аналитической платформы, использованной в процессе моделирования РЭС
Например, зная зависимость выходной мощности РЭС от радиации, можно оценить критическое значение её уровня, при котором выходной параметр системы выходит за допустимые пределы, и соответствующим образом оптимизировать конструктивно-технологические решения для РЭС. При этом, работая с готовой моделью, построенной аналитиком, разработчику, конструктору и технологу не требуется вникать во все детали процесса моделирования.
Экспериментальная часть
Пусть имеется набор из k измерений состояния параметров моделируемой РЭС, содержащий n параметров. Например, если таким набором является БД результатов измерений параметров однотипных РЭС, то каждым наблюдением будет являться серия измерений n параметров устройств, входящих в систему. В процессе исследования производились измерения параметров для фазовращателей – среднеквадратическое отклонение (СКО) по разрядам фазы, начальные потери (Lн), коэффициент стоячей волны (КСВН); для аттенюаторов – СКО по разрядам амплитуды, Lн, КСВН; для усилителей мощности – выходная мощность, ток потребления, коэффициент усиления, уровень компрессии, КСВН; выходные параметры всей системы – выходная мощность, фаза, КПД, КСВН, коэффициенты усиления, шума и др. Тогда каждое наблюдение может быть представлено в виде n-элементного вектора z. В соответствии с логикой решаемой задачи параметры моделируемой системы разделяются на две группы: входные (независимые) и выходные (зависимые). Например, выходная мощность зависит от потерь.
Вектор признаков z может быть разделен на два вектора: входных x = (x1, x2, ..., xn) и выходных y = (y1, y2, ..., yn) параметров. Таким образом, каждое наблюдение, сформированное на основе серии измерений набора параметров для конкретного устройства, представляет собой обучающий пример zi = (xi, yi), в котором для каждого входного воздействия x определено значение целевого вектора y. Задача заключается в том, чтобы, последовательно предъявляя модели наблюдения, обучить ее на каждое входное воздействие xi формировать отклик 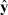 , максимально близкий к фактическому yi.
, максимально близкий к фактическому yi.
Зависимость между множеством входных параметров РЭС и выходными характеристиками обычно носит сложный нелинейный характер. Это вызвано совместным влиянием параметров, а также наличием других факторов, влияющих на результирующие характеристики (несовершенство технологии, температура, радиация, влага, вибрация, ударная нагрузка и другие). Поэтому для восстановления зависимости между выходными характеристиками и множеством входных параметров РЭС использовалась нейросетевая модель.
На основе результатов измерений 50 изделий был сформирован обучающий набор примеров, содержащих шесть признаков. В качестве нейросетевой архитектуры модели была выбрана плоскослоистая НС следующей конфигурации: число входных нейронов равно числу входных параметров модели – 6, а выходных – одному (коэффициент усиления). Число скрытых нейронов выбиралось исходя из правила, что общее количество связей НС должно быть в 2–3 раза меньше числа примеров обучающего множества. Поэтому была выбрана сеть с одним скрытым слоем, содержащим 5 нейронов (что обеспечивает 25 связей) и логистической активационной функцией.
Обучение НС производилось по алгоритму обратного распространения ошибки с использованием 10000 итераций. Среднеквадратическая ошибка оценивания между фактическими и предсказанными значениями выходного параметра составила 5 %. Практическое использование модели при дальнейших исследованиях РЭС позволило снизить требуемое число измерений на 23 %.
Заключение
В статье рассмотрена возможность использования интеллектуальных методов моделирования при разработке сложных РЭС. Целью исследования являлось изучение перспектив снижения затрат на контроль параметров устройств РЭС на основе моделирования зависимостей между ними. Предложена конфигурация аналитической платформы с разделением функций аналитика и инженерных специалистов. Проведены экспериментальные исследования моделирования РЭС по шести входным параметрам на основе нейронной сети. Практическое использование модели подтвердило эффективность и адекватность подходов и методов, предложенных в работе.
Рецензенты:
Жулев В.И., д.т.н., заведующий кафедрой информационно-измерительной и биомедицинской техники, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань;
Корячко В.П., д.т.н., профессор, заведующий кафедрой «Системы автоматизированного проектирования вычислительных средств», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Работа поступила в редакцию 28.05.2014.



