Пусть A дифференциальный оператор
(1)
определенный на множестве функций D(A) ∈ L2 [0, 1] и непрерывные на [0, 1] вместе со своими производными до четвертого порядка включительно и удовлетворяют некоторым граничным условиям, например
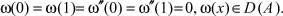(2)
И пусть q(x) ≥ 0 на интервале (0, 1).
Такое множество D(A) является линейным многообразием, всюду плотным в гильбертовом пространстве L2[0, 1].
Определение. Линейный симметричный оператор A называется положительным, если для любого u ∈ D(A) выполняется неравенство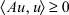 
, причем 
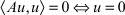[1, 2].
Из определения следует, что A –положительно определенный оператор.
Рассмотрим операторное уравнение в гильбертовом пространстве L2 [0, 1] с оператором (1)
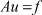. (3)
Теорема. Уравнение (3) с положительным оператором A имеет не более одного решения в D(A).
Доказательство. Допустим, что операторное уравнение (2) имеет два решения u1 и u2. Тогда Au1 = f или
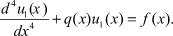
Аналогично Au2 = f или
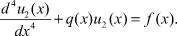
Вычи:
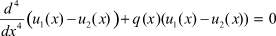
или
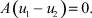
Из последнего равенства следует, что
Из приведенного выше определения положительности получаем, что и это равносильно тому что
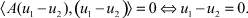
Таким образом, u1 = u2.
Уравнением (1) описывается, например, поперечный прогиб u(x) балки [3] под действием распределенной поперечной нагрузки f(x), f(x) ∈ L2(0, 1), где балка имеет постоянную жесткость на изгиб и лежит на упругом основании, реакцию которого определяет слагаемое q(x)u(x), q(x) ≥ 0 на интервале (0, 1).
При таком физическом смысле постановки задачи граничные условия отражают то, как закреплены ее концы. Так, для консольной балки с жестко защемленным левым и свободным правым концами граничные условия имеют вид
Если балка имеет на концах опоры, допускающие (в отличие от жесткого защемления) поворот ее поперечного сечения, пропорциональный в этом сечении изгибающему моменту, то в этом случае граничные условия принимают следующий вид:
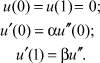
Из этих уравнений при α = β = 0 вытекают условия жесткого защемления, а при α → ∞ и β → ∞ – шарнирного опирания, и условия принимают вид (2).
Рассмотрим функционал вида
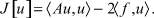(4)
Справедлива следующая теорема о квадратичном функционале.
Теорема. Для того, чтобы элемент u0 ∈ D(A) был решением операторного уравнения (1) необходимо и достаточно, чтобы квадратичный функционал (4) на u0 принимал свое минимальное значение в D(A), т.е.
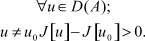
Доказательство: Необходимость. Пусть на элементе u0 функционал (4) принимает минимальное значение в D(A), т.е.
Используя свойства скалярного произведения и симметричности положительного оператора, получаем:
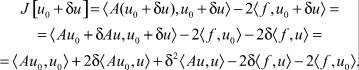
При u ≠ 0;
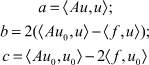
правая часть полученного выражения является квадратным трехчленом
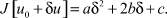
Данный трехчлен свое минимальное значение принимает при δ = 0
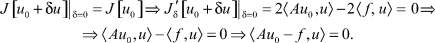
Последнее равенство означает, что элемент Au0 – f ∈ L2[0, 1] является нулевым элементом этого пространства, так как оно верно ∀u ∈ D(A) ⊂ L2[0, 1], т.е. Au0 – f = 0, а значит u0 ∈ D(A) является решением (1).
Достаточность. Функционал (4) определен при всех u ∈ D(A). Пусть u0 удовлетворяет (1): Au0 = f. Подставляя это значение вместо f в (4), получаем:
Отсюда
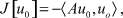
и в силу положительности оператора A имеем
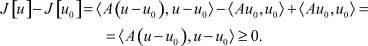
Так как
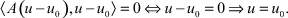
Теорема доказана.
При таком раскладе решения операторного уравнения (3) можно построить итерационный процесс [1] со скоростью геометрической прогрессии, с помощью которого можно найти минимальный элемент специального вида функционала, поиск которого является эквивалентным поиску минимального элемента функционала (4).
Введем оператор А0 следующим образом: обозначим
u(4) = v,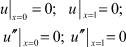 
или в операторной форме
A0u = ν,
где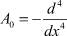 
– оператор однозначно разрешим в пространстве L2(0, 1) с заданными краевыми условиями.
Тогда уравнение (3) примет вид
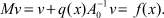(5)
Если v найдено, то u вычисляется по формуле
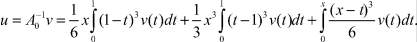
Обозначим
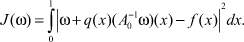(6)
При ω = ν, где ν ‒ решение (5), имеем J(ω) = 0 и наоборот.
Будем предполагать, что уравнение (5) для любой правой части f(x) ∈ L2(0, 1) имеет единственное решение. Следовательно, из теоремы Банаха вытекает, что
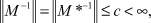(7)
где 
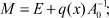(8)
и норма 
– вычисляется явно в пространстве L2(0, 1).
причем
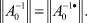
Построим итерационный процесс.
Пусть ωn n-е приближенное решение уравнения J(ωn) = 0.
Положим
ω n+1 = ωn – εω,
где ε – положительное число.
Тогда
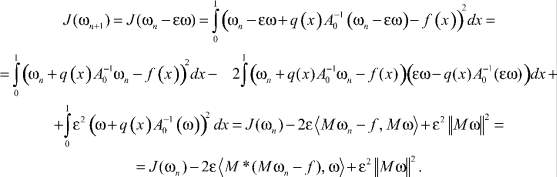
Мы воспользовались линейностью интегрального оператора A0.
Выберем
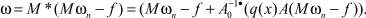
Тогда
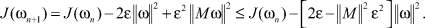(9)
В силу условия (1.11) имеем
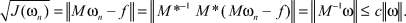
Поэтому из (1.13) следует
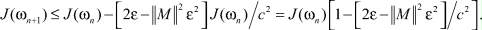
Выберем
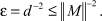
Тогда получим
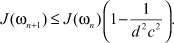(10)
Для разности ωn+1 – ωn имеем
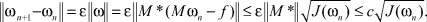
Это неравенство и (10) дают следующий результат:
Теорема 1.2.1. Пусть для любого f(x) ∈ L2(0, 1) задача (3) имеет единственное решение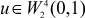 
, причем оператор M, определенный по (5), удовлетворяет условиям 
, причем справедливо неравенство cd > 1. Тогда для любого ω0 ∈ L2(0, 1) последовательность, определяемая по формулам
,
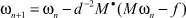сходится к решению ω• уравнения (1.9’), причем выполнены оценки
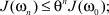
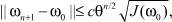
где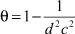 
. При этом функция u = A–1 ω• будет решением задачи (5).
Доказательство. Из (10) и последующих неравенств следует, что
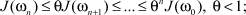
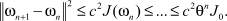
Докажем сходимость приближенного решения к решению исходной задачи:
{ωn} – фундаментальная последовательность, L2(0, 1) – полное гильбертово пространство, тогда существует такой элемент ω•, что ωn → ω• в L2(0, 1) и из непрерывности оператора M получим J(ωn) → J(ω•). Тогда из первого неравенства теоремы следует, что J(ω•) = 0, то есть Mω• = f и u = A–1ω•.
Теорема доказана.
Рецензенты:
Оразбаев Б.Б., д.т.н., профессор, Атырауский институт нефти и газа, академик ИА РК, г. Атырау;
Хасанов А., д.ф.-м.н., профессор, Актюбинский университет им. С. Баишева, г. Актобе.
Работа поступила в редакцию 21.05.2014.