В данной работе рассматриваются аспекты моделирования сетевых систем, причем именно сетевые признаки являются наиболее существенными для адекватного составления математических моделей. Эти признаки существенно отличают предлагаемый далее подход от методов моделирования, общепринятых, например, в теории систем и теории автоматического управления, основными инструментами которых являются интегро-дифференциальные уравнения, методы теории вероятностей, математической статистики и случайных процессов. В теории систем и теории автоматического управления обычным описанием исследуемой системы является описание «вход-выход», а изменение выхода относительно входа, то есть пространство состояний системы задается передаточными функциями в матричном виде. Большинство систем, являющихся объектами моделирования, являются нелинейными, и в данном случае существенные усилия моделирования направлены на линеаризацию систем, выполняемую путем решения систем дифференциальных уравнений в матричном виде. Результатами моделирования являются восстановленное фазовое пространство моделируемых систем и характеристики звеньев управления и регулирования.
Другой подход к моделированию сетевых систем использует методы теории систем и сетей массового обслуживания, в которых рассматриваются различные модели входных, выходных потоков и правил обслуживания, построенных на базе соответствующих законов распределения случайных величин и процессов. В данном случае методами моделирования являются генераторы некоторых типов случайных процессов (имитирующих моменты времени поступления заявок на обслуживание), а результатами моделирования являются (часто усредненные) времена пребывания заявки в очереди, системе, времена обслуживания, вероятности пребывания в очереди, вероятности обслуживания (за некоторый период) и другие вероятностные и статистические характеристики.
Заметим следующее: и в общей теории систем, и в теории систем и сетей массового обслуживания неявно предполагается использование процессного времени. Это означает, что в первом случае принимается, что процессы в системах протекают по возможности мгновенно (хотя в некоторых случаях допустима их инерционность), а во втором случае принимается, что процессы подчинены некоторому вероятностному закону. Однако во втором случае иногда рассматривают потоки general (общего) типа, в которых основным соотношением является рекуррентное уравнение Линдли [7], что по сути близко к рассматриваемому нами далее подходу с идейной стороны, но не со стороны реализации методов моделирования. В целом процессное время означает, что изменение состояний системы, а также её модели можно отметить на некоторой временной шкале, если шкала является непрерывной, то естественным будет непрерывное моделирование состояний системы, иначе – дискретное моделирование состояний системы, а также соответствующий им математический аппарат.
В основу дискретно-событийного моделирования, развиваемого появления известной системы GPSS [1] и сетей Петри [5] положена другая концепция: состояния системы изменяются под воздействием некоторых событий, в общем случае безотносительно их точной привязки к временной шкале. Существенными являются лишь факты наличия возникновения этих событий и взаимодействие их между собой, то есть синхронизация (некоторое событие предшествует другому, некоторое событие вызывает возникновение другого, либо других событий и так далее). Для сетевых компьютерных систем как многопользовательских многозадачных, многомашинных, многопроцессорных систем характерным является еще один аспект событийности – конкуренция за сетевые распределенные вычислительные ресурсы, с целью увеличения производительности, минимизации простоев и тому подобное. Оба этих аспекта – синхронизация и конкуренция – делают сетевые компьютерные системы существенно нелинейными, что усложняет их аналитическое и имитационное моделирование, а рассматриваемый далее в работе подход можно рассматривать как возможную линеаризацию таких систем.
В итоге введения к статье следует заметить, что научные исследования в области дискретно-событийного моделирования сейчас достаточно широко развиты в различных направлениях [13, 10], а также служат как существенное дополнение методов имитационного моделирования систем. Существуют также программные реализации дискретно-событийных систем моделирования, например AnyLogic, SimPy, SimEvents и другие. Однако в рамках данной статьи нас интересует вполне самостоятельное направление дискретно-событийного моделирования с применением алгебраических структур (max,+) подхода [9], который, на наш взгляд, адекватно отражает поставленную в названии статьи проблему – моделирование высоконагруженных сетевых компьютерных систем.
Применение метода (max,+) алгебры в дискретно-событийном моделировании
Основной структурой в рассматриваемом подходе является (max,+) полукольцо [9], являющееся числовым множеством (с элементами из множества ¡, включая –∞ и не включая +∞ ), снабженным операциями «максимума», играющего роль «сложения» и «сложения», играющего роль «умножения». Указанные операции (max,+) в специализированной литературе [9, 6] обозначаются соответственно ⊕ и ⊗ (то есть имеют другое значение в отличие от общепринятых – прямой суммы и прямого произведения матриц), то есть x⊕y = max{x, y}, x⊗y = x + y. Данное (mах,+) полукольцо является идемпотентным [6], то есть сложение a⊕a = a является идемпотентным, нулем считается ε = –∞, единицей, считается e = 0, которая нейтральна по операции ⊗, а для каждого ненулевого элемента по этой операции имеется обратный элемент. Для обеих операций выполняется коммутативность и ассоциативность, а операция ⊗ дистрибутивна относительно ⊕. Такая алгебраическая структура часто называется диоидом [11]. Аналогичный подход с использованием (min,+) алгебраических структур рассмотрен в работе автора [8].
Данные свойства указанной алгебраической структуры оказываются существенно полезными для дискретно-событийного моделирования сетевых компьютерных систем с точки зрения оценки и достижения их максимальной производительности. Рассмотрим простой пример дискретно-событийного моделирования автоматизированной системы управления контейнерными перевозками (АСУ КП) на железнодорожном транспорте. В моделируемой системе имеются автоматизированные рабочие места (АРМ) работников АСУ КП на двух железнодорожных станциях:
1) узловой станции Ростов-Товарная;
2) припортовой станции Новороссийск.
Посредством единой сети передачи данных ОАО «РЖД» АРМы АСУ КП работают в сетевом режиме и между ними передается информация, сопутствующая технологическому процессу обработки документов. Будем рассматривать 4 события (конечно, в существенно упрощенной форме), соответствующие работе оператора АРМ АСУ КП:
1) подготовка пакета исходной документации с телеграмм-натурным листом поезда;
2) ввод и передача информации в сетевом режиме АРМ АСУ КП на первой станции;
3) прием и распечатка входящей документации с телеграмм-натурным листом поезда;
4) подтверждение и корректировка принятых данных в АРМ АСУ КП на второй станции.
Естественным образом устанавливается порядок синхронизации событий, так, например, подтверждение и корректировка данных могут произойти не ранее, чем данные вообще будут получены, а подготовка документации может происходить не ранее прибытия поезда с контейнерами. Для того, чтобы не ограничиваться одним направлением и подчиняться общим принципам моделирования систем на рисунке показаны технологические процессы с АРМ АСУ КП на станциях и названы в целом «подготовкой данных». Различное время технологических операций на станциях, а также приема и передачи в разных направлениях может быть обусловлено различной производительностью АРМов, различным опытом операторов и другими аналогичными причинами. Приемы моделирования различных событий, связанных с интенсивной нагрузкой информационных систем и программного обеспечения, рассматривались ранее в работах автора [2, 4].
Для дальнейшей определенности и конкретных расчетов положим, что время подготовки документации на железнодорожные платформы с контейнерами в АРМ АСУ КП занимает у оператора xA = 3 минуты; ввод данных на каждый вагон формируемого поезда из 60 вагонов на станции Ростов-Товарная составляет yBA = 12 минут при отправке телеграмм-натурного листа на станцию Новороссийск. Время, затрачиваемое на формирование принятого на припортовой станции Новороссийск телеграмм-натурного листа контейнерного поезда, составляет xB = 2 минуты, а время, затрачиваемое на согласование корректировок со станцией Ростов-на-Дону и внесение их в АРМ АСУ КП на станции Новороссийск, составляет yBA = 10 минут.
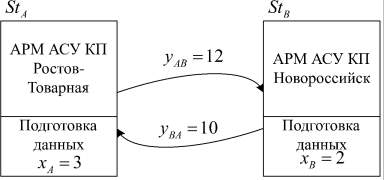
Графическая иллюстрация упрощенного технологического процесса контейнерной перевозки между станциями StA и StB
Поставим цели моделирования, состоящие в нахождении максимальных нагрузок на сетевые компьютерные АРМы АСУ КП при выполнении следующих ограничений:
1) нормативы времени на технологические операции, выполняемые операторами АРМ АСУ КП на станциях, являются максимально допустимыми;
2) операторы АРМов приступают к формированию пакетов поездной документации только после прибытия поезда, однако между технологическими операциями задержек не возникает;
3) интенсивность обработки документаций в АРМах должна учитывать максимальную производительность контейнерных перевозок, а следовательно, и максимально возможное количество поездов, курсирующих на участке между StA и StB.
Смоделируем времена tA отправления пакетов с телеграмм-натурными листами поездной документации со станции StA. Пусть для начального условия tA(0) = 0, а, учитывая заданные ранее значения времени подготовки, ввода, обработки и корректировки данных, следует, что очередной пакет поездных документов отправится не ранее, чем будет сформирован, то есть
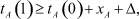 (1)
(1)
а очередной прибывший пакет поездных документов будет обработан не ранее, чем будут переданы предыдущие корректировки на станцию StA со станции StB:
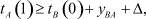 (2)
(2)
где tB(0) – начальный момент времени отправления корректировок со станции StB, который можно принять tB(0) = 0, Δ – некоторая временная задержка в технологических процессах на транспорте. Выражения (1) и (2) можно записать в более общем виде:
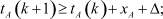 (3)
(3)
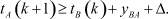 (4)
(4)
Приняв Δ = 0 и подставив значения из примера из (3) и (4), получим, что максимальная задержка отправления составит
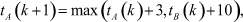 (5)
(5)
а для станции StB аналогично (1)–(4)
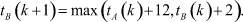 (6)
(6)
Так же как и в работе [12], для k = 0, 1, 2, ... по (5) и (6) рассчитаем последовательность tA = {0, 10, 22, 32, ...} и tB = {0, 12, 22, 34, ...}.
Заметим, что выражения (3)–(4) и соответствующие им выражения (5)–(6) с подставленными в них максимальными значениями временных интервалов xA, xB, yAB, yBA можно переписать в общем виде следующим образом.
Пусть имеется n станций ti, t = 1, ..., n, а времена, необходимые на технологические операции по перемещению контейнерной документации между i-й и j-й станциями, обозначим zij, тогда (5) и (6) имеет вид
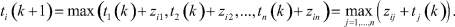 (7)
(7)
Выражение (7) можно сравнить с выражением для линейной рекуррентной последовательности [3] следующим образом:
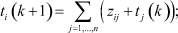 (8)
(8)
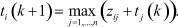 (9)
(9)
В (9) применим метод (max, +)-алгебры, а для того, чтобы подчеркнуть дальнейшую возможность использования методов линейной алгебры в (max, +)-алгебре, выражение (9) запишем как
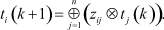 (10)
(10)
Также, по аналогии с линейной алгеброй, выражение (10) можно записать в матричном виде:
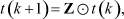 (11)
(11)
где e – (max, +) – операции; Z – матрица, содержащая коэффициенты преобразований.
Рассчитаем в соответствии со значениями в приведенном выше примере по (11) матрица коэффициентов преобразований будет содержать времена технологических операций, поэтому
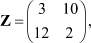
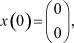
таким образом,
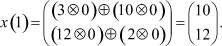
Далее, принимая во внимание, что
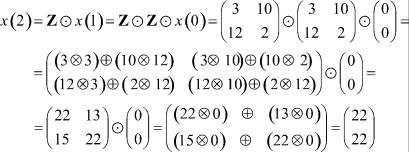
и так далее.
Заключение
Дискретно-событийное моделирование с использованием (max,+) подхода является достаточно эффективной технологией моделирования систем с синхронизацией событий, Эта технология является пригодной для моделирования сетевых компьютерных систем, в частности АРМов и АСУ, применяемых на железнодорожном транспорте для определения режимов их функционирования в условиях максимальных нагрузок.
Работа выполнена при финансовой поддержке РФФИ, проекты 13-01-00325-а, 13-01-00637-а.
Рецензенты:
Павлов И.В., д.ф.-м.н., профессор, заведующий кафедрой высшей математики Ростовского государственного строительного университета, г. Ростов-на-Дону;
Чернов А.В., д.т.н., профессор, заведующий кафедрой прикладной математики и вычислительной техники Ростовского государственного строительного университета, г. Ростов-на-Дону.
Работа поступила в редакцию 21.05.2014.



