В настоящей работе проводится определение основных параметров распространяющихся в земной коре сейсмо-акустических волн путем решения обратной задачи [2, 5]. Для регистрации сейсмо-акустических волн на основе явления двойной модуляции мессбауэровского излучения [6] в ИППФ НАН РА были разработаны уникальные детекторы. Полученные результаты теоретических расчетов достаточно близки с полученными экспериментальными данными.
Определение параметров и вида сейсмо-акустических волн на основании мессбауэровских спектров поглощения, модулированных акустическими колебаниями, часто сводятся к решению обратных задач. Трудности решения обратных задач во многих случаях обусловлены их некорректной постановкой [2, 4, 5].
Для определения закона возбуждения рассмотрим форму линии поглощения при внешнем периодическом возбуждении [1, 3, 6, 7]
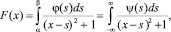(1)
где F(x) – мессбауэровский спектр поглощения с некоторой ошибкой; φ(s) – закон возбуждения,
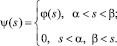
Умножая обе части уравнения (1) на exp(+ipx), интегрируя по x и используя обратное Фурье преобразование, получаем
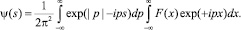(2)
Однако вычисление Ψ(s) из (2) представляет определенные трудности, т.к. для сходимости интеграла необходимо, чтобы экспериментальная функция F(x) была гладкой функцией. Даже маленькая ошибка в F(x) приводит к большому искажению Ψ(s) из-за члена exp|p|. Эти трудности можно преодолеть при помощи метода регуляризации [5], развитой для решения некорректно поставленных обратных задач.
Для определения значения Ψ(s) рассмотрим «регуляризационный» функционал
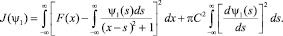(3)
Функция Ψ1 является регуляризованным решением и лишена вышеуказанных недостатков.
Таким образом, учитывая, что функционал J имеет минимум и что Ψ1 (±∞) = 0 или Ψ′1(±∞) = 0, из условия минимума J имеем
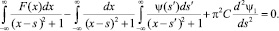(4)
Для ψ1(s) получаем
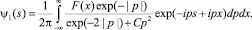(5)
Как и ожидалось, это выражение совпадает с выражением (2) при условии C = 0. Анализируя далее экспериментальные случаи с четной функцией F(x), имеем
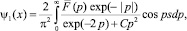(6)
где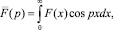 
которая вычисляется метод Филона и значение C определяется из экспериментальной ошибки.
При некоторых асимметричных случаях закона возбуждения задача сводится к решению интегрального уравнения
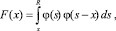
который решается численными методами.
Метод математической обработки модулированных временных мессбауэровских спектров для определения неизвестных параметров внешних возбуждений заключается в согласовании экспериментальных точек Nk = N(tk) некой аналитической функцией Ñ = Ñ(tk; α1, α2,…, αn), где tk – время, α1, α2,…, αn – неизвестные параметры внешних возбуждений. Точное определение параметров α1, α2,…, αn сводится к подбору согласующей функции для получения наилучших совпадений экспериментальных точек Nk с согласующими функциями Ñ(tk; α1, α2,…, αn).
Согласующую функцию для временных мессбауэровских спектров можно описать следующим выражением
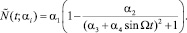(7)
Для подбора параметров аппроксимирующей функции минимизируется следующий неотрицательный функционал
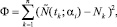
где n – число экспериментальных точек, для которых выполняется условие
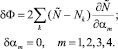(8)
Отсюда для параметров αi получаем следующую систему уравнений
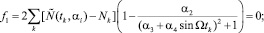
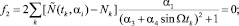
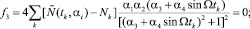
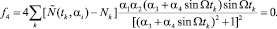(9)
Получается система нелинейных алгебраических уравнений для параметров α1, α2, α3 и α4, при решении которой используется метод квазилинеаризации Ньютона – Рапсона, т.е. выбираются начальные приближенные значения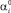 
и разлагается fj(αi) в ряд в окрестности точки 
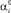. Оставляя только линейный член, получаем
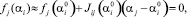i = 1, 2, 3, 4, (10)
где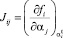 
– матрица Якоби.
Решение этой системы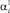 
является первым приближением параметров αi
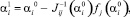(11)
где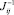 
– обратная матрица Якоби.
Найденные таким образом решения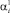 
снова подставляются в первоначальную систему уравнений (9) для нахождения второго приближения 
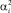. Решения 
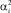снова подставляются в (9) и находится следующее приближение и т.д. Окончательно для α1, α2, α3 и α4 в n-м приближении имеем
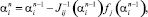, i,j = 1, 2, 3, 4. (12)
а
б
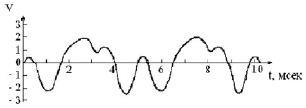
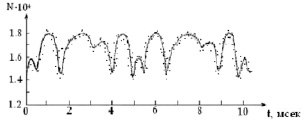
Закон движения источника гамма-квантов (а) и временной мессбауэровский спектр поглощения (б): V – скорость движения источника гамма-квантов; t – время; N – количество гамма-квантов, зарегистрированных детектором
Точность определения исходных параметров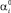 
зависит от реальных условий эксперимента и полученных экспериментальных данных, так как в реальном физическом эксперименте величины Nk определяются с некоторой погрешностью, определяемой статистическим набором гамма-квантов, которая и может привести к соответсвующим ошибкам в определении αi.
На рисунке а приведено заданное нами движение источника гамма-квантов, а на рисунке б – временной мессбауэровский спектр поглощения гамма-квантов, регистрированных с помощью детекторов, разработанных в ИППФ НАН РА. Как видно из этих рисунков, имеется достаточно хорошее совпадение измеряемого сигнала с законом движения источников гамма-квантов.
Заключение
Проведенный сравнительный анализ показывает, что, применяя представленный математический аппарат при обработке экспериментальных данных временной мессбауэровской спектроскопии путем решения обратной задачи можно определить основные параметры низкочастотных сейсмо-акустических колебаний и восстановить вид колебаний.
Рецензенты:
Ванцян А.А., д.ф.-м.н., профессор, ведущий научный сотрудник, Институт прикладных проблем физики Национальной академии наук Республики Армения, г. Ереван;
Саарян А.А., д.ф.-м.н., профессор, Ереванский государственный университет, г. Ереван.
Работа поступила в редакцию 15.05.2014.