Методам построения уравнений динамики шарнирных многозвенных механизмов, являющихся механической основой манипуляционных систем промышленных роботов, посвящена обширная литература. Одна из основных целей авторов, работающих в этом направлении, – создание наиболее эффективных алгоритмов формирования динамических уравнений для таких механизмов. Сравнительный анализ [1] показывает существенную зависимость эффективности различных подходов от числа N звеньев кинематической цепи механизма и его геометрии; для N = 2−6 вполне приемлемым оказывается использование Лагранжевского описания динамики механизма.
В данной работе дифференциальные уравнения динамики механизма строятся на основе уравнений Лагранжа 2-го рода, в которых для выражения кинетической энергии использован набор линейно независимых тригонометрических функций обобщенных координат [3]. Использование таких функций существенно упрощает алгоритм формирования системы дифференциальных уравнений динамики механизма.
Построение математической модели
Рассматривается движение плоского трехзвенного механизма, шарнирно связанного с неподвижным основанием (рис. 1). Звенья 1, 2, 3 - абсолютно твердые тела, которые перемещаются в горизонтальной плоскости под действием моментов М1, М2, М3 в шарнирных сочленениях О1, О2, О3 (рис. 1). С каждым звеном свяжем локальную систему координат Оkxkyk, ось Оk xk которой проходит через оси сочленений звена, а для конечного звена (k = 3) направляется произвольно (рис. 1); О0x0y0 - неподвижная инерциальная система координат. Известны массы звеньев mk, положения их центров масс Ck, и центральные моменты инерции Ik относительно осей перпендикулярных плоскости движения; считаем эти оси главными осями инерции звеньев.
За обобщенные координаты приняты углы взаимного поворота звеньев q1, q2, q3, отсчитываемые против хода часовой стрелки (рис. 1).
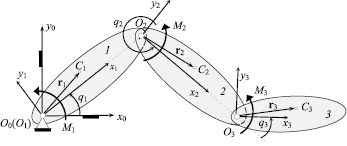
Рис. 1. Расчетная схема механизма
Кинетическая энергия Т механизма складывается из кинетических энергий его звеньев:
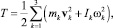(1)
где vk – скорость центра масс k-го звена, а
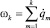(2)
‒ угловая скорость k-го звена в неподвижной системе отсчета О0 x0y0.
Кинетическая энергия рассматриваемой механической системы является положительно определенной квадратичной формой обобщенных скоростей, коэффициенты которой зависят от обобщенных координат [4]:
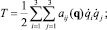
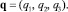(3)
Чтобы исследовать структуру выражений aij(q), представим скорости vk центров масс звеньев в виде рекурсивных соотношений:
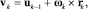(k = 1, 2, 3);
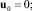
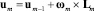(m = 1, 2), (4)
где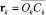 
– радиус-векторы центров масс звеньев; 
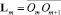– радиус-векторы центров шарнирных сочленений звеньев; um – скорости центров сочленений Оm; ωk – вектор угловой скорости k-го звена.
При использовании плоских систем координат Оkxkyk и двухкомпонентных векторов удобно представить (4) в матричной форме
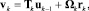(k = 1, 2, 3);
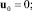
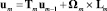(m = 1, 2). (5)
Здесь координаты векторов скоростей vk и um представлены в локальных системах координат Оkxkyk и Оmxmym соответственно;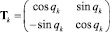 
– матрица преобразования координат вектора из системы Оk−1xk−1yk−1 в Оkxkyk ; 
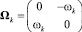– кососимметричная матрица угловой скорости k-го звена;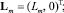 
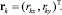Последовательно применяя (5), получаем:
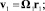
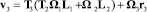
или в покомпонентной записи
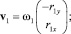
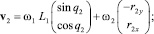
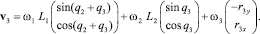(6)
Используя (6), находим выражения для квадратов скоростей центров масс звеньев:
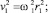
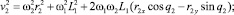
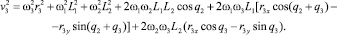(7)
Равенства (7) (2) и (1) позволяют установить, что в выражении (3) для кинетической энергии механизма коэффициенты аij(q) при обобщенных скоростях могут содержать линейные комбинации только следующих семи линейно независимых функций обобщенных координат
α1 = 1, α2(q2) = cos q2; a3(q2) = sin q2;
α4(q3) = cos q3; α5(q3) = sin q3;
α6(q2, q3) = cos (q2 + q3);
α7(q2, q3) = sin (q2 + q3), (8)
которые назовем базисными функциями, т.е.:
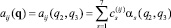
(i, j = 1, 2, 3). (9)
Чтобы найти постоянные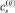 
в (9), воспользуемся приемом, предложенным в работе [5] для вычисления элементов матрицы инерции системы сочлененных тел.
Обозначим Tij(q) величину кинетической энергии механической системы, находящейся в произвольной заданной конфигурации q = (q1, q2, q3) и имеющей обобщенные скорости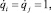 
(k ≠ i, j). Значения Tij(q) нетрудно вычислить с помощью полученных ранее соотношений (1), (2) и (6). После этого числовые значения всех коэффициентов aij(q) можно последовательно найти, используя равенства
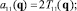
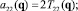
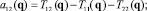
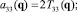
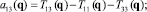
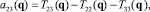
следующие из (3).
Пусть найдены значения aij(q) для семи различных конфигураций рассматриваемой механической системы, тогда постоянные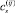 
(s = 1, …, 7) в разложении (9) можно найти, решая систему линейных алгебраических уравнений
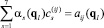(l = 1, …, 7)
с ненулевым определителем
,
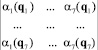где q1, ..., q7 – различные конфигурации манипулятора. Чтобы отыскать все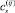 
, учитывая симметрию коэффициентов aij(q), достаточно сформировать и решить 6 таких систем.
Для описания динамики механизма воспользуемся уравнениями Лагранжа 2-го рода:
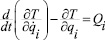(i = 1, 2, 3), (10)
где Qi = Mi – обобщенные силы, равные моментам, действующим в сочленениях.
Вычисляем производные, входящие в левые части уравнений (8):
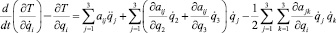
или, учитывая (9) и (8):
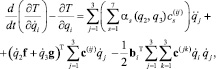(11)
где
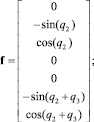
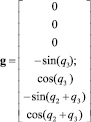
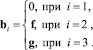
С учетом (11) дифференциальные уравнения (9) принимают вид:
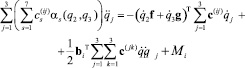(i = 1, 2, 3). (12)
Система трех обыкновенных дифференциальных уравнений 6-го порядка (12) с начальными условиями
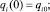
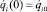(i = 1, 2, 3) (13)
является математической моделью, описывающей динамическое поведение плоского шарнирного трехзвенника при заданных моментах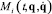 
в сочленениях.
Численная реализация модели
Для интегрирования полученной системы дифференциальных уравнений была использована явная конечно-разностная схема Рунге ‒ Кутты 4-го порядка с постоянным временным шагом. Размер шага интегрирования выбирался в ходе численных экспериментов. Дифференциальные уравнения динамики манипулятора (13) не являются разрешенными относительно вторых производных, поэтому на каждом временном шаге значения обобщенных ускорений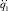 
, 
, 
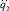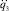находились в результате решения линейной системы
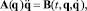
где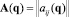 
– матрица инерции механизма; B – вектор правых частей уравнений (12).
В приводимом ниже примере расчета использовались следующие значения геометрических и инерционных параметров звеньев механизма: m1 = 10 кг, m2 = 10 кг, m3 = 8 кг; Lk = 1 м;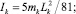 
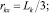
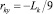(k = 1, 2, 3).
Момент M1, действующий в сочленении O1, задавался в виде
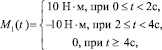(13)
т.е. соответствовал управляющему моменту, который обеспечивает поворот твердого тела вокруг неподвижной оси на конечный угол.
Для моментов, действующих в сочленениях O2 и O3, принималось соответственно:
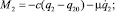
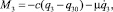(14)
где с = 10 Н∙м/рад; m = 20 Н∙м/рад∙с−1.
Первые слагаемые в выражениях (14) соответствуют моментам упругой реакции сочленений, препятствующей взаимному повороту звеньев, зафиксированных в положениях q2 = q20, q3 = q30. Вторые слагаемые в (14) соответствуют моментам сил сопротивления пропорциональным угловым скоростям взаимного поворота звеньев.
Начальные значения обобщенных координат и скоростей механизма:
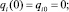
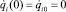
(i = 1, 2, 3). (15)
На рис. 2 представлены результаты численного интегрирования уравнений (11) при начальных условиях (15) и обобщенных силах (13), (14).
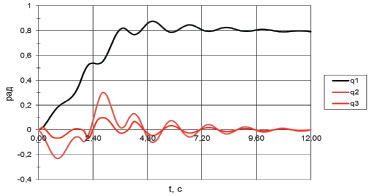
Рис. 2. Изменение обобщенных координат трехзвенника: q1(t), q2(t), q3(t)
Кривые на рис. 2 изображают происходящие со временем изменения обобщенных координат q1, q2, q3 соответственно. Поведение механизма соответствует ожидаемому повороту на конечный угол. Наблюдаемое затухание колебаний обусловлено диссипативными моментами (14), действующими в сочленениях О2 и О3.
На компьютере с процессором Intel, имеющем рабочую частоту 2,8 ГГц при временном шаге интегрирования Δt = 0,02 с, расчет движения механизма продолжительностью 12 с в среде Mathcad 7.0 занимает около 1 с машинного времени.
Заключение
Предложенный способ формирования дифференциальных уравнений динамики плоского шарнирного многозвенного механизма позволяет избежать вывода громоздких символьных выражений [2] для вычисления элементов матрицы инерции, а также центробежных и гироскопических членов. В то же время в ходе численного интегрирования уравнений динамики расчет текущих значений всех членов и коэффициентов уравнений на каждом временном шаге выполняется по явно заданным конечным формулам без использования рекурсивных алгоритмов [5]. Представляется перспективным использование данного подхода для описания динамики плоских шарнирных механизмов с числом звеньев N > 3.
Работа выполнена в рамках задания № 2014/217 на выполнение государственных работ в сфере научной деятельности в рамках базовой части государственного задания Минобрнауки России.
Рецензенты:
Полянин И.А., д.т.н., профессор кафедры транспортных и технологических машин, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;
Сидыганов Ю.Н., д.т.н., профессор кафедры эксплуатации машин и оборудования, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Работа поступила в редакцию 15.05.2014.