Проблема природных катаклизмов крайне важна, так как последствия данных явлений очень тяжелы во многих сферах жизни общества, как с точки зрения биологических жертв, так и с точки зрения экономического ущерба. В частности, к таким проблемам относят и проблему лесных пожаров. При возгорании леса, где убытки становятся колоссальными, в целых краях и областях объявляется режим чрезвычайного положения. Вследствие этого перед наукой стоит проблема моделирования пожаров и способов его тушения.
Лесной массив будем моделировать многофазной однотемпературной однородной пористой реагирующей средой [5]. Положим лес продуваемым массивом, по сравнению с объемной долей газовой фазы будем считать объёмную долю конденсированной фазы лесных горючих материалов пренебрежимо малой [2, 4]. Будем считать, что пожар начинается в условиях уже сформировавшегося поля скоростей. Температуру очага в течение заданного времени примем постоянной величиной, его форму будем считать прямоугольной, давление в начальный момент времени полагается равным атмосферному [3]. Процесс считаем независимым от координаты y. Расчеты проводились для характерных типов растительности Высокоборского лесхоза Нижегородской области [6]. Лес считается однородным по всей высоте. Предполагаем, что вода подается в точку прицела с заданной интенсивностью, а размер капель таков, что они долетают до цели и полностью испаряются.
Высокоборское лесничество находится в заволжской части Нижегородской области. Его географические координаты 56°30′ с. ш. и 44°50′ в. д. По ботанико-географическому районированию оно располагается в пределах подзоны хвойно-широколиственных (подтаежных) лесов. Преобладающими почвообразующими породами являются флювиогляциальные пески. Ландшафтная структура территории лесничества такова. В центральной его части распространены сосновые молодняки и болота на флювиогляциальных песках. Это зандровая равнина, сформированная во время таяния московского ледника. В северной части заповедника распространены леса со значительным участием неморальных видов, что обуславливается произрастанием их на двучленных отложениях, состоящих из моренного суглинка или супеси, перекрытых сверху истонченным плащом флювиогляциального песка [7]. Рельеф лесничества в основном равнинный, но встречаются нерезкие холмы и овраги. По климатическим условиям территория лесничества может быть отнесена к атлантико-континентальной климатической области [1]. Средняя температура января – –10 °С, июля – 18,1 °С, средняя годовая – 3,6 °С. Осадки выпадают преимущественно в теплый период года. Среднегодовое количество осадков составляет 628 мм.
Для моделирования тушения фронта пожара будем использовать характеристики водных пушек. Будем считать, что в наличии имеется достаточное количество пушек, расположенных вдоль всей линии фронта пожара с заданным интервалом так, чтобы вода подавалась с максимально эффективной интенсивностью. Считаем, что подача заданного количества воды водной пушкой осуществляется в точку прицела с разбросом по нормальному закону:
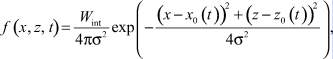
где x0(t), z0(t) – координаты точки прицела водной пушки; Wint – массовый расход воды на метр фронта, кг/(м·с); σ, м – среднеквадратическое отклонение, обуславливающее дальность разлёта частиц воды от точки прицела.
В качестве точки прицела используется ближайшая к водной пушке по оси x точка в слое леса, температура которой больше критической величины Tcr. В случае, когда несколько точек удовлетворяют данному условию, в качестве прицела выбирается точка с наибольшей высотой. Данная двумерная постановка своим главным достоинством имеет возможность выбора критического значения температуры и анализа алгоритмов подачи воды в область пожара, а также позволяет выбирать высоту подачи воды. Если вода подается недостаточно интенсивно, чтобы потушить пожар, пламя продвигается, но много медленней.
Рассмотрим динамику огня при Tcr = 450 К и Wint = 1,25 кг/(м·с). Результаты показали, что в данном случае при подаче такого количества воды тушения не происходит.
По мере распространения пламени несущественно меняются области высоких температур. В очаге пожара и потоке продуктов горения значительно возрастает скорость газовой фазы.
Расчеты показали, что для эффективного тушения при Tcr = 450 К необходимо Wint = 2,38 кг/(м·с). При таком раскладе точка разрыва фронта пожара появляется в момент времени 6 с. Потери энергии во фронте пожара на испарение попавшей воды приводят к замедлению скорости его распространения. Часть фронта огня в середине полога леса тушит вода при 6,8 с, причем оставшиеся части очага не могут выделить достаточной энергии для продолжения пожара и компенсации энергии, затраченной на испарение поступающей воды. Вследствие этого лесной пожар довольно быстро затухает.
Как показали расчеты, тушение пожара при Tcr = 800 К требует меньше воды (Wint = 1,73 кг/(м·с) и более эффективно. Динамика тушения при вышеописанных параметрах представлена на рис. 1.
Верхняя часть фронта пожара срезается на первоначальном этапе, но из-за того, что конвекция быстро разогревает верхнюю часть слоя лесных горючих материалов, это не ведет к тушению огня. В момент времени 1,2 с фронт пожара становится устойчивым. Однако уже при 1,6 с температура уменьшается, вследствие чего скорость распространения огня и способность противостоять поступающей воде уменьшаются. Как видно из рисунка, на момент времени 2,8 с, в нижней части фронта пожара имеет место вспышка, но так как там сконцентрирован обстрел водной пушкой, пламя затухает.
При Tcr = 1500 К динамика распространения пожара описана ниже, при этом Wint = 2,68 кг/(м·с). Разрыв фронта пожара происходит на начальном этапе подачи воды при 0,8 с, температура в верхней части полога леса значительно падает. В приземную зону перемещается прицел подачи воды при 1,6 с.
При температуре ниже 1500 К вода прекращает подаваться. Однако во фронте пожара температура достаточно высокая для возобновления горения, а в момент времени 2,4 с повышается по всей высоте огня. Прицел водной пушки перемещается в приземный слой, и температура в нём существенно снижается при 3,2–4,8 с, после чего распространение пламени прекращается, так как температура огня недостаточна для его продолжения.
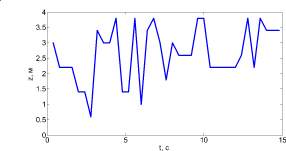
Случай, когда интенсивность подачи воды выше и ниже критической, показан на рис. 2. До 0,3 с на графиках отсутствуют линии, так как на момент готовности водной пушки пожар вне зоны досягаемости струи воды.
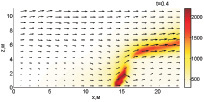
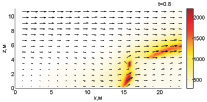
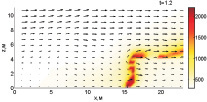
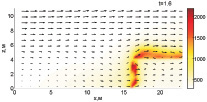
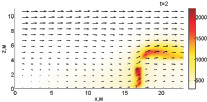
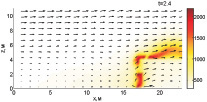
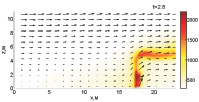
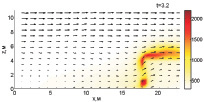
Рис. 1. Динамика распространения пожара при Tcr = 800 К, Wint = 1,73 кг/(м·с)
 а
а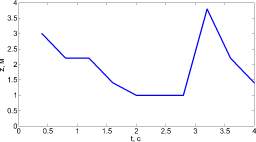 б
б
Рис. 2. Динамика движения точки прицела подачи воды при Tcr = 800 К:
а – Wint = 1,72кг/(м·с); б – Wint = 1,73кг/(м·с)
Рис. 2, а показывает, что при малой интенсивности подачи воды, точка прицела носит хаотичный характер. В таком случае классически точкой прицела выбираются точки из верхней части полога лесного массива. На рис. 2, б на начальном этапе подачи воды динамика точки прицела аналогична рис. 2, а, однако можно наблюдать достаточно долгий промежуток времени подачи воды в нижнюю часть фронта пожара (2–2,8 с) рис. 2, б. Малые температуры сосредоточены в нижней части полога лесного массива к моменту 2 с. Энергия в меньшей степени распространяется вверх из-за подачи воды, что тормозит распространение пожара.
Таблица демонстрирует результаты численных экспериментов по моделированию тушения пожара при помощи заданного потока воды в данной постановке.
Зависимость эффективности подачи воды в зависимости от значения критической температуры
|
Критическая температура, К |
Критическая интенсивность подачи воды, кг/(м·с) |
|
500 |
2,111 |
|
600 |
1,885 |
|
800 |
1,726 |
|
900 |
1,759 |
|
1500 |
2,677 |
Итак, полученные результаты показали, что тушение пожара максимально эффективно при температуре 800 К, а использование в качестве прицела точек с температурой ниже или выше 800 К приводит к увеличению интенсивности подачи воды. Это связано с тем, что вода расходуется на охлаждение растительности в кромке пожара.
Если в данную область не подавать воду, то часть энергии теряется за счет внешнего поля скоростей. Выбор зоны низких температур в качестве точки прицела не ведет к сильному росту необходимой интенсивности подачи воды. Если точкой обстрела принять область высоких температур, то есть ядро очага, тогда энергия, затрачиваемая на излучение, приводит к уменьшению рассеивания.
Важно отметить, что интенсивность излучения, в соответствии с законом Стефана ‒ Больцмана, пропорциональна четвёртой степени температуры, что предполагает увеличение интенсивности подачи воды. Распространение лучистой энергии происходит менее интенсивно, это ведет к уменьшению её потерь и некоторому торможению распространения пожара. Увеличение количества воды позволяет остановить распространение пожара.
Рецензенты:
Петрухин Н.С., д.ф.-м.н., ординарный профессор Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород;
Карпухин В.Б., д.ф.-м.н., доцент, профессор Московского государственного университета путей сообщения, Российская открытая академия транспорта, г. Москва.
Работа поступила в редакцию 07.05.2014.



