Лесные пожары зачастую являются источником чрезвычайных экологических ситуаций и всегда наносят огромный вред окружающей среде — от выбросов продуктов горения в атмосферу до полного уничтожения растительного покрова на значительных площадях. Лесные пожары нарушают сложившееся экологическое равновесие и наносят экономический ущерб лесному хозяйству, а также угрожают жизни местного населения [1, 2]. В разных типах лесов и местности развитие пожара может происходить по различным сценариям, поэтому при их моделировании необходимо учитывать как внешние факторы, так и структуру лесного ландшафта [3].
Проблема борьбы с лесными пожарами была и остаётся актуальной. Важной составляющей её эффективного решения является прогнозирование развития пожаров, позволяющее принять наиболее эффективные меры по их тушению. Численное моделирование лесных пожаров, благодаря современным высокопроизводительным электронным вычислительным машинам, позволяет проанализировать ключевые сценарии развития ситуации. Несмотря на высокую производительность современных компьютеров, для таких задач, как моделирование распространения лесных пожаров, остаётся актуальной проблема оптимизации, которая помимо алгоритмических подходов может решаться за счёт размещения данных в памяти [4, 8]. Для решения задачи был использован метод крупных частиц [6].
Для тушения пожара используется водяная пушка, которая движется вдоль фронта пожара с заданной скоростью. Для моделирования такого сценария тушения используется физико-математическая постановка [5, 8], применяемая к плоскости y = y1, где ось Oy направлена горизонтально поперёк фронта пожара. В дальнейшем y = y1 будем называть плоскостью моделирования. Для учёта воды, попадающей в плоскость моделирования, используется двумерное изотропное распределение Гаусса с точкой прицела (x0, y0), где y0 определяется движением водяной пушки вдоль фронта пожара, а x0 по максимальной температуре в плоскости моделирования. Для моделирования взаимодействия воды, падающей сверху, используется алгоритм, приведённый в работе [5, 7].
При моделировании тушения пожара с помощью источника подачи воды предполагалось, что её составляющая скорости вдоль фронта пожара не может превышать 20 м/с, что связано с техническими сложностями в обеспечении подачи достаточного количества воды. Минимальная рассматриваемая скорость составила 0,5 м/с. Это обусловлено увеличением времени подачи воды в плоскость y = y1, которое обратно пропорционально скорости движения источника подачи воды и необходимостью увеличения размеров расчётной области для моделирования распространения пожара в течение больших промежутков времени. С другой стороны, передвижение источника подачи воды с такой низкой скоростью нецелесообразно, так как расход воды на тушение фронта заданной длины многократно возрастает в таком случае.
На рис. 1–2 показана динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 60 кг/с и скоростью движения водяной пушки 3,13 м/с. В момент времени 1 с в плоскость y1 попадает незначительное количество воды, что приводит лишь к некоторому снижению температуры. По мере увеличения количества поступающей в плоскость моделирования пожара воды существенно уменьшается интенсивность пожара в его верхней части. Также можно видеть разрыв конвективной колонки. В результате интенсивной подачи воды в зону горения очаг сужается и становится ниже к моменту 3 с.
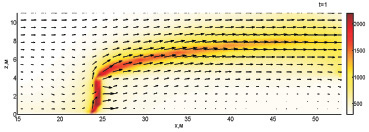
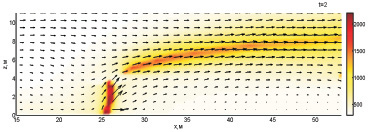
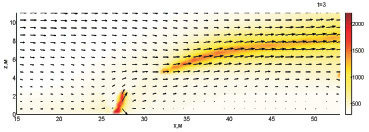
Рис. 1. Динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 60 кг/с и скоростью движения водяной пушки 3,13 м/с (1–3 с)
Даже при некотором удалении водяной пушки от плоскости y1 небольшая интенсивность брызг, долетающих до очага горения, препятствует его разгоранию. В результате этого на момент 4 с очаг продолжает сжиматься. Тем не менее в дальнейшем очаг расширяется (5 с) и происходит
его развитие.
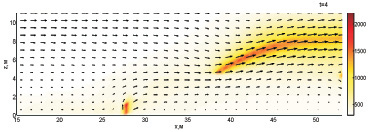
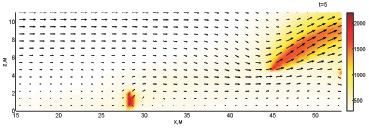
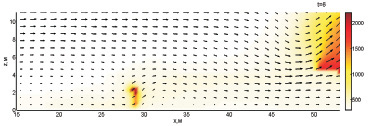
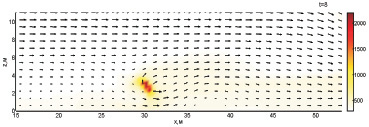
Рис. 2. Динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 60 кг/с и скоростью движения водяной пушки 3,13 м/с (4-8 с)
Численное моделирование взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 60 кг/с и скоростью движения водяной пушки 3,128 м/с показало, что до момента 2 с его поведение практически идентично результатам, приведённым на рис. 2. Это связано с незначительностью отличия в количестве воды, поданной в область пожара. Однако уже на момент времени 3 с можно заметить некоторые отличия от аналогичного результата для случая с более быстрым движением водяной пушки. Тем не менее такие, казалось бы, незначительные отличия в динамике пожара приводят в дальнейшем к существенным отличиям. Более слабый очаг пожара, оставшийся на момент 3 с, уже не обеспечивает достаточное количество энергии для поддержки своей температуры при подаче воды. С другой стороны, меньшая скорость движения пушки увеличивает время подачи воды, хотя и незначительно в данном случае, но вполне достаточно, чтобы прекратить горение. После момента 4 с происходит рассеивание остатков тепла и продуктов горения.
Динамика пожара в большой степени зависит от интенсивности потока воды и времени его действия. В связи с этим интерес представляет динамика пожара при потоке воды 120 кг/с и высоких скоростях движения водяной пушки. На рис. 3 показана динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 120 кг/с и скоростью движения водяной пушки 15,567 м/с.
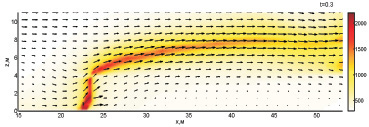
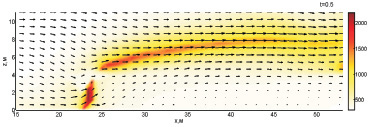
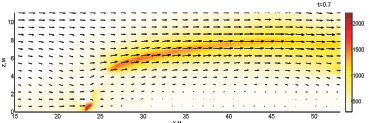
Рис. 3. Динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 120 кг/с и скоростью движения водяной пушки 15,567 м/с (0,3–0,7 с)
Как следует из постановки задачи, прицел водяной пушки оказывается в плоскости моделирования пожара в момент 0,5 с. Ключевое отличие динамики пожара при большей интенсивности потока воды сводится к изменению масштабов времени процессов кипения подаваемой в пожар воды и развития пожара. При большей интенсивности подачи воды пожар не успевает существенно развиться и выделить энергию, защищающую его очаг от капель воды.
На рис. 4 можно видеть динамику восстановления пожара из очага, оставшегося после тушения.
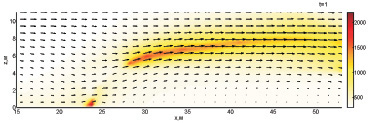
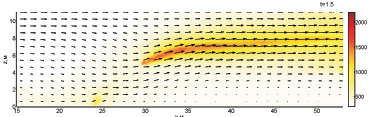
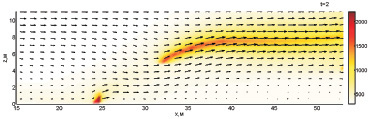
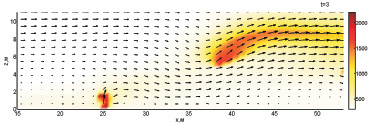
Рис. 4. Динамика взаимодействия пожара с водой при обстреле по центру ядра пожара с интенсивностью 120 кг/с и скоростью движения водяной пушки 15,567 м/с (1–4 с)
На момент 1 с подача воды в плоскость моделирования пожара прекращается практически полностью. Энергия оставшегося очага пожара сначала распределяется на прогрев впереди находящегося слоя растительности (1,5 с), затем очаг пожара
существенно нагревается к моменту 2 с. На момент 3 с очаг начинает распространяться вперёд и вверх, после чего фронт восстанавливается и процесс пожара продолжается.
Как можно видеть, динамика пожара при различных значениях интенсивности подачи свободной воды имеет много общего. По мере приближения точки прицела к плоскости моделирования происходит тушение верхней части слоя лесных горючих материалов. Основная часть очага пожара тушится, когда прицел близок к плоскости моделирования. Оставшаяся часть очага тушится, когда пушка вновь отдаляется от плоскости. В случае, если скорость движения водяной пушки существенно ниже критической, прекращение пожара происходит намного раньше. Это уменьшает скорость тушения пожара и снижает эффективность использования воды.
Следует отметить, что увеличение расхода воды, подаваемой водяной пушкой, приводит к значительному увеличению критической скорости её движения. Вода поступает сверху, расходуясь на охлаждение конвективной колонки, и в случае меньшей интенсивности подачи до очага пожара доходит лишь небольшая часть воды. Это приводит к уменьшению требуемого на метр длины фронта количества воды.
Согласно данным, приведённым в работе [2], расход воды на площадь кромки лесного пожара составляет около 5 кг/м2. По расчётам, приведённым в работе Абдурагимова [1], на прекращение пламенного килограмма топлива с теплотой сгорания 40–50 МДж/кг за счёт охлаждения пламени требуется 2 литра воды, отмечая, что на практике это значение в 5–10 раз выше, Принимая во внимание, что в проведённых расчётах плотность лесных горючих материалов составляет 8 кг/м2, а их теплотворная способность 11 МДж/кг. Таким образом, принимая во внимание плотность и учитывая поправку на его теплотворную способность, можно получить расчётное значение требуемого количества воды на уровне 4 кг/м2. Учитывая ширину кромки пожара 1–1,5 м, расход воды составит 4–6 кг/м. Расчёты, представленные в работе, учитывают не все факторы, приводящие к недостаточному эффективному использованию воды, имеющие место на практике. Так, например, в данной статье учитывается расход воды на преодоление области нагретой газовой фазы в верхней части полога леса, но используется упрощённая модель рассеивания воды на основе изотропного двумерного распределения Гаусса, то есть с одинаковой дисперсией по каждой из координат. В модели не рассматривается динамика капель различных размеров, вместо этого предполагается, что капли долетают до цели и там полностью испаряются.
Рецензенты:
Карпухин В.Б., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика», Российской открытой академии транспорта Московского государственного университета путей сообщения, г. Москва;
Петрухин Н.С., д.ф.-м.н., ординарный профессор Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород.
Работа поступила в редакцию 07.05.2014.



