Присоединенной массой называется величина, имеющая размерность массы, которая добавляется к массе тела, движущегося неравномерно в жидкой или газообразной среде, для учета воздействия среды на это тело. При этом считается, что тело в жидкости или газе движется под действием внешних сил так же, как оно двигалось бы под действием этих сил в пустоте, если бы его масса изменилась на величину присоединенной массы [1]. Для сферы присоединенная масса составляет половину массы среды, вытесненной сферой. Для плоской квадратной пластины с площадью сечения S эта эффективная масса составляет μ=πρS3/2/4 , где ρ - плотность среды [2]. То есть для пластины площадью S=0.038м2, движущейся в воздухе, это - 7.5г. Существенно отметить, что присоединенная масса является постоянной величиной, не зависящей ни от скорости, ни от характера движения. Если это действительно так, если учет присоединенной массы полностью описывает воздействие среды на движущееся тело, то колебания протяженного тела массой m в воздухе (рис. 1) должны быть незатухающими:
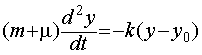 , (1)
, (1)
где k - жесткость пружины, у0 - положение равновесия, отвечающее условию
![]() ,
,
у0 - длина нерастянутой пружины.
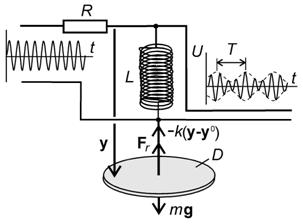
Рис. 1. Схема эксперимента
Совершенно очевидно, что уравнение (1) должно быть дополнено силой аэродинамического сопротивления [3]:
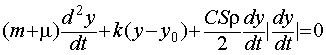 . (2)
. (2)
При этом снова возникает противоречие: коэффициенты аэродинамического сопротивления C [4] получены продувкой тел различной формы в аэродинамической трубе, что соответствуют установившемуся режиму обтекания. Колебательный характер движения тела установившимся можно назвать с очень большой натяжкой. Для плоского диска такой коэффициент аэродинамического сопротивления составляет C≈1.1. Однако, в динамическом режиме, то есть при падении тела в поле гравитационных и диссипативных сил он оказался равным 2.7 [5]. Различие оказалось слишком большим, чтобы на него не обратить внимание. К сожалению, остался открытым вопрос и о влиянии присоединенной массы на параметры, характеризующие падение тел при наличии сил сопротивления воздуха. Указанные выше противоречия могут быть устранены только экспериментально.
Схема эксперимента достаточно проста и показана, по существу, на рис. 1. Это - простейшая RL-цепь, в которой роль индуктивности играет упругий элемент (пружина) L, а сопротивление резистора составляет величину около 1кОм. Коэффициент жесткости пружины k=9.6 Н/м, коэффициент затухания гармонических колебаний (величина обратная промежутку времени, за который амплитуда уменьшается в e раз) не более 0.005. Эффективная масса тела, участвующего в гармонических колебаниях, учитывающая, в том числе и массу пружины, поэтому, равна
![]() , (3)
, (3)
где T0 - экспериментальное значение периода гармонических колебаний. Примерно таким же выражением определяется период затухающих колебаний, в которых должна участвовать присоединенная масса m, следовательно
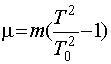 . (4)
. (4)
Здесь T - экспериментальное значение периода затухающих колебаний. Разумеется, выражение (4), определяющее присоединенную массу, предполагает, что увеличение периода, обусловленное затуханием, мало. Это допущение, после того как будет определен коэффициент аэродинамического сопротивления, должно быть специально аргументировано. Амплитуду падения переменного напряжения U с несущей частотой 4 кГц на индуктивности можно существенно увеличить, установив внутрь пружины ферритовый сердечник с достаточно большой магнитной проницаемостью.
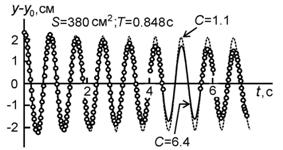
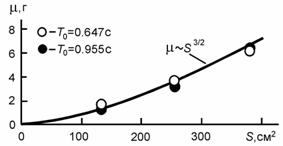
На рис. 2 показана восстановленная зависимость удлинения пружины от времени для T0=0.833 с, что соответствует массе m=169 г. Отсюда μ=6.1 г. Это - первый результат. Следующий вывод оказался оказался более, чем неожиданным. Традиционные экспериментальные данные по коэффициентам аэродинамического сопротивления [4] неприменимы для описания колебаний протяженных тел. В данном случае колебания происходят с коэффициентом сопротивления, почти в шесть раз превышающем значение C, полученное продувкой пластины в аэродинамической трубе. Этот эффект является чрезвычайно важным, поэтому должен быть подробно изучен. Однако, сначала следует вернуться к полученному значению присоединенной массы и проверить, насколько корректна оценка (4). Здесь достаточно добавить, что решение дифференциального уравнения (2) при указанных выше параметрах, но T=0.840c, дает увеличение периода, обусловленное затуханием, не более чем на 0.06%. Оценка присоединенной массы, судя по всему, является достаточно правильной. Это позволяет определить величину присоединенной массы для других размеров тонкого диска и частот колебаний. На рис. 3 показаны экспериментальные значения присоединенной массы в зависимости от площади диска S для двух значений периода T0. Похоже, что присоединенная масса действительно является постоянной для данного тела величиной. Однако к количественному совпадению c теоретическими выводами [2] следует, вероятно, относиться как к случайному. В появлении присоединенной массы нет ничего необычного. Это - эффективная масса среды, которой тело передает импульс при своем движении. Присоединенная масса в данной задаче определяет изменение частоты колебаний и не более.
|
|
|
|
Рис. 2. Пример зависимости удлинения пружины от времени. Точки - экспериментальные результаты, штриховая кривая - решение дифференциального уравнения (2) для коэффициента аэродинамического сопротивления C=1.1 , сплошная кривая - то же для С=6.4 |
Рис. 3. Присоединенная масса тонкого диска при различных периодах колебаний и площадях сечения |
Следующий, достаточно важный результат, - независимость коэффициента аэродинамического сопротивления от площади сечения S и сравнительно слабая зависимость от частоты затухающих колебаний (рис. 4). Основное здесь даже не в том, что в зависимости от периода колебаний T коэффициент C имеет экстремум, а в необычно большом его значении. Среднее значение коэффициента С составляет величину 6.5 , превышающее традиционное значение CT=1.1 почти в шесть раз. По крайней мере это так, при частотах колебаний около 1 Гц. Судя по всему, мы имеем дело с динамическим режимом, существенно отличающимся от статического, которому отвечают результаты измерений в аэродинамических трубах.
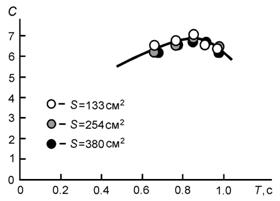
Рис. 4. Экспериментальная зависимость коэффициента аэродинамического сопротивления С от периода затухающих колебаний T при различных площадях диска S
Следует признать, что пока не понятно, как строго решить обратную задачу: их экспериментальных данных, аналогичных представленным на рис. 2, получить зависимость силы аэродинамического сопротивления от скорости. Поэтому в данной работе был использован наиболее простой подход. Предполагая, что зависимость силы сопротивления от скорости является квадратичной, определялись такие значения T и C, при которых согласие экспериментальных результатов с решением дифференциального уравнения (2) оказывается наилучшим. Конечно, такой подход может встретить много нареканий. Но именно квадратичная зависимость силы сопротивления от скорости используется в большинстве аэродинамических расчетов. В том числе это относится и к вибрационному режиму [6].
СПИСОК ЛИТЕРАТУРЫ
- Седов Л.И. Механика сплошной среды. Том. 2. М.: "Лань", 2004. 560 c.
- Седов Л.И. Плоские задачи гидродинамики и аэродинамики. М.: Наука, 1966. 448 с.
- Стрелков С.П. Механика. М.: Наука, 1975. 560 с.
- Sovran G., Morel T., Mason W.T. Aerodynamic Drag Mechanisms of Bluff Bodies and Road Vehicles. New York: Plenum Press, 1978. 360 p.
- Герасимов С.А. Аэродинамика зонтообразного тела с квадратичным сопротивлением движению. // Полет. 2006. № 10. С. 55-57.
- Герасимов С.А., Удалова Е.С. Критический режим вибрационного полета с квадратичным сопротивлением движению. // Техника и технология. 2005. № 1. С. 17-20.