Работа выполнена в «МАТИ» – Российском государственном технологическом университете им. К.Э. Циолковского. При раскатке (рис. 1, а) элемент трубчатой заготовки помещают между двумя роликами, которые под действием усилия Р деформируют стенку заготовки, увеличивая ее диаметр. Известна раскатка заготовок, когда взамен наружного ролика используется вращающее кольцо или матрица (рис. 1, б) [1, 2]. В последнем случае исходная заготовка имеет первоначально меньший диаметр и раскатывается до внутреннего диаметра кольца (матрицы), что повышает точность изготовления детали.
Недостатком приведенных схем, изображенных на рис. 1, является то, что они предназначены для деформирования элементов трубчатых заготовок.
Для деформирования концевых участков длинномерных труб перспективными являются процессы раскатки, изображенные на рис. 2–3 [5, 6].
Эти процессы раскатки дают принципиальную возможность получать детали типа переходник в условиях сжатия материала в очаге деформации, что, как известно, значительно повышает предельные возможности формоизменения концевого участка трубы. Кроме того, они могут применяться после традиционного процесса раздачи труб на жестком пуансоне, что даст возможность получать переходники с большим суммарным перепадом диаметров. Однако процессы, приведенные на рис. 2 и 3, еще не достаточно исследованы в технологическом плане.
Таким образом, проведенный литературный анализ технологии получения деталей типа переходник показал, что наибольшее распространение получили процессы раздачи труб на жестком пуансоне. Процессы локального деформирования, включая раскатку труб, в настоящее время практически не используются. Не используются также процессы последовательного совмещения раздачи и раскатки труб.
Исходные уравнения равновесия для решения плоской задачи в цилиндрических координатах имеют вид (рис. 4).
а б
Рис. 1. Схема раскатки кольцевых заготовок: а – между двумя роликами; б – между кольцом и роликом; 1 – ролики; 2 – заготовка; 3 – кольцо (матрица)
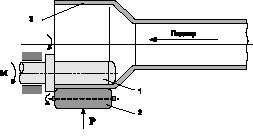
Рис. 2. Схема перспективного процесса раскатки труб с подпором кромки по патенту РФ № 2104112: 1 – ведущая оправка; 2 – ведомая давильная оправка; 3 – деформируемая заготовка
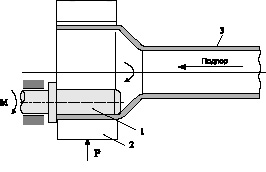
Рис. 3. Схема перспективного процесса раскатки труб с подпором кромки и давильным кольцом: 1 – ведущая оправка; 2 – ведомое давильное кольцо; 3 – деформируемая заготовка
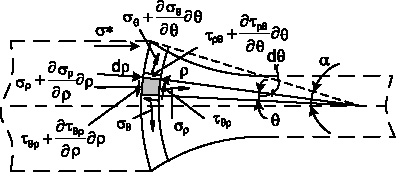
Рис. 4. К расчету напряженно-деформированного состояния
(1)
Приближенное условие пластичности для зон отставания и опережения запишем в виде
(2)
Поставим (2) в первое уравнение системы (1), получим расчетные выражения для расчета напряженного состояния внутренних слоев заготовки в виде
(3)
(4)
Совместное решение (3) и (4) может быть приведено к виду [2]:
(5)
Решение уравнения (5) относительно τρθ приводится к выражениям:
(6)
где С1, С2 – произвольные постоянные, определяемые из граничных условий по ρ; С3, С4 – произвольные постоянные, определяемые из граничных условий по Θ; n1, n2, m – коэффициенты, причем 
; σ* – напряжение подпора при ρ = R, причем σ* = σ*(θ).
Точное аналитическое решение системы (6) практически не представляется возможным из-за большого числа произвольных постоянных, включая неизвестную функцию подпора σ* = σ*(θ).
В ряде работ систему (6) решают, вводя дополнительные допущения. Поэтому решим исходную систему уравнений (3) и (4) применительно к плоскости симметрии заготовки, допуская различный линейный закон изменения τρθ по координатам.
Допустим, что для заготовок, когда длина очага деформации «а» соизмерима с толщиной стенки S, величина τρθ по толщине (по Θ) и по радиусу ρ не меняется в середине очага деформации. Тогда уравнения (1) и (2) запишутся в виде
(7)
(8)
(9)
Совместное решение (7) и (9) приводится к виду
(10)
где σ* – напряжение подпора на входе в середине очага деформации.
Заметим, что из условия равновесия величина напряжения подпора σ* в середине очага деформации и на свободных поверхностях при линейном распределении σ* будет отличать знаком (рис. 5).
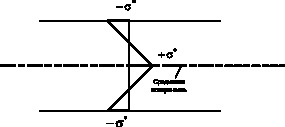
Рис. 5
Уравнение (8) используем как оценочное. Пусть величина τρθ близка к максимальному значению, тогда (8) будет иметь вид 
. То есть для малых углов Θ, лежащих в пределе 0–0,15 радиан, изменение σθ от величины τρθ будет незначительным (до ±15 % от σS).
Решение (10), приведенное совместно с распределением напряжений на контактных поверхностях, показано на рис. 6–8.
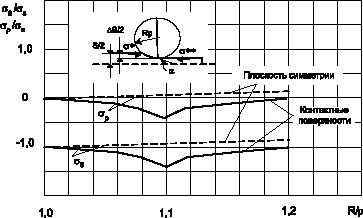
Рис. 6. Распределение напряжений по зонам очага деформации зависимости от напряжений подпора (α/μ =0,225; S/2 = 1,0 мм; ΔS/2 = 0,2 мм; Rp = 12 мм; σ*/σS = σ**/σS = 0)
Вывод
Из приведенных графиков распределения напряжений видно, что напряженное состояние в срединной части заготовки отличается от распределения напряжений на поверхностях контакта главным образом тем, что в срединной части заготовки возникают растягивающие радиальные напряжения, величина которых увеличивается как по направлению к выходу заготовки из очага деформации, так и с увеличением напряжений подпора перед входом в очаг деформации σ* и выходом из него σ**.
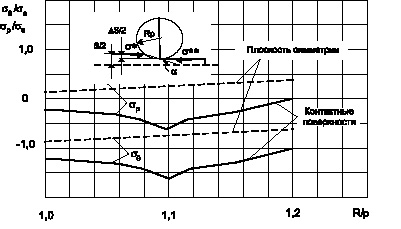
Рис. 7. Распределение напряжений по зонам очага деформации зависимости от напряжений подпора (α/μ =0,225; S/2 = 1,0 мм; ΔS/2 = 0,2 мм; Rp = 12 мм; σ*/σS = –0,2; σ**/σS = 0)
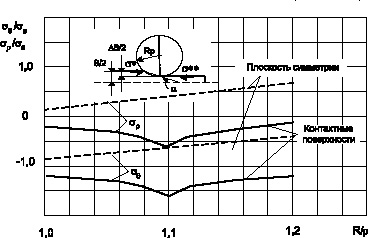
Рис. 8. Распределение напряжений по зонам очага деформации зависимости от напряжений подпора (α/μ =0,225; S/2 = 1,0 мм; ΔS/2 = 0,2 мм; Rp = 12 мм; σ*/σS = σ**/σS = –0,2)
Рецензенты:
Гагарина Л.Г., д.т.н., профессор, зав. кафедрой «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета МИЭТ, г. Москва;
Симаранов С.Ю., д.т.н., профессор, генеральный директор ЗАО «Техноконсалт», г. Москва.
Работа поступила в редакцию 18.04.2014.