Работающий тиристорный электропривод оказывает на питающую сеть неблагоприятное воздействие. Одним из видов такого воздействия являются высокочастотные искажения напряжения питания. В синусоидальном напряжении сети появляются так называемые коммутационные провалы, оказывающие на другие потребители электрической энергии вредное влияние. Основным фактором, определяющим глубину этих провалов, является величина индуктивности сети, которая, в свою очередь, зависит от соотношения первичных и вторичных индуктивностей рассеяния питающего трансформатора [2, 3]. Соотношение первичных и вторичных индуктивностей рассеяния питающих трансформаторов также важно знать при расчетах электропривода переменного тока. Проблему можно решить, используя теорию неоднозначности составляющих индуктивностей рассеяния трансформаторов.
Экспериментальное определение характеристик коммутации вентилей
При исследовании можно пренебречь активными сопротивлениями обмоток трансформаторов и падением напряжения в вентилях при протекании по ним рабочего тока. Для выполнения опыта используется экспериментальный тиристорный электропривод постоянного тока (рис. 1), питаемый от трансформатора, в котором определяется соотношение первичных и вторичных индуктивностей рассеяния. В качестве нагрузки тиристорного преобразователя используется электродвигатель постоянного тока (ДПТ). Его мощность может быть в несколько раз меньше мощности электропривода, который будет установлен в действительности для реализации нужной технологии. Должна быть предусмотрена возможность плавно регулировать вращающий момент ДПТ. Для этого вал двигателя механически соединяется с валом генератора (ГПТ), тормозной момент которого плавно регулируется.
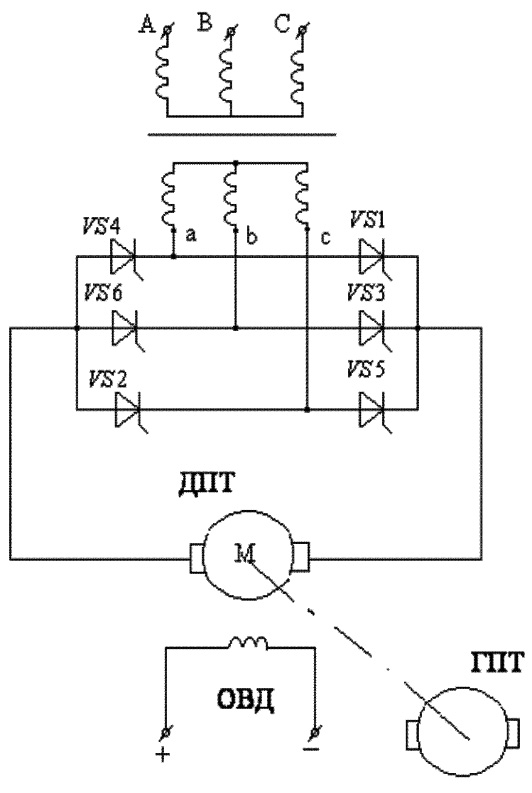
Рис. 1. Трехфазная электрическая схема ТП для снятия характеристик коммутации вентилей
Первый этап эксперимента – определение совместного индуктивного сопротивления рассеяния трансформатора и сети (χγ), влияющего на процесс коммутации фазных токов. Производится разгон электропривода до максимально возможной скорости. При этом угол управления ТП должен быть близок к нулевому значению (α ≈ 0). Затем осуществляется увеличение момента сопротивления на валу двигателя путем воздействия на тормозной момент генератора. Ток нагрузки устанавливается приблизительно на уровне Id ном двигателя. Снимаются замеры: действующее значение линейного напряжения питания тиристорного преобразователя U2, тока нагрузки двигателя Id, и по осциллографу, включенному на напряжение нагрузки, измеряются величины угла управления α и угла коммутации γ. По этим данным, используя формулу
,
определяется индуктивное сопротивление коммутирующего контура χγ.
Если α = 0, величина χγ определяется по более простой формуле:
Индуктивное сопротивление χγ определяет процесс коммутации токов с учетом неоднозначности составляющих суммарного индуктивного сопротивления χ2 и χ1Σ. Для определения индуктивного сопротивления короткого замыкания трансформатора и сети нужно знать величину отношения:
Здесь χ2 – индуктивное сопротивление рассеяния вторичных обмоток трансформатора; 
– коэффициент трансформации питающего трансформатора; χ1Σ – суммарное индуктивное сопротивление первичных обмоток трансформатора с индуктивным сопротивлением сети
χ1Σ = χ1ТР + χc.
Для вычисления Nkγ производится второй этап эксперимента. Воздействуя на СИФУ ТП, угол управления α устанавливается равным 
. При этом Ud = 0 и Id = 0. Эксперимент проводится при неподвижном заторможенном якоре электродвигателя. Затем, постепенно уменьшая угол α, увеличивают ток якоря до значения, при котором он становится непрерывным, а на экране осциллографа, включенного на напряжение нагрузки, отчетливо просматривается коммутация токов в виде кратковременного импульса. В трехфазной мостовой схеме мгновенные значения выпрямленного напряжения ub в зоне коммутации не равны полусумме ЭДС коммутируемых фаз [1]. Напряжение ub смещается в отрицательную или в положительную сторону от среднего значения. Эти смещения чередуются в четных и нечетных импульсах пульсаций напряжения. В рассматриваемой схеме на каждом такте переключений в коммутации участвуют две фазы. Одна из них коммутирует с отставанием от предыдущей коммутации этой фазы на угол Ψ1 = 60°, другая – на угол Ψ2 = 120°.
На рис. 2 приведена диаграмма напряжения на нагрузке, имеющая место в этой схеме при переключениях фаз (α ≈ 90°). Участвующие в коммутациях фазы обозначены a, b, c. Дальше от нулевой линии коммутирует фаза с отставанием на данном такте от предыдущей коммутации этой фазы на угол Ψ1 = 60°, ближе к нулевой линии – фаза с отставанием Ψ2 = 120°. Величина индуктивности коммутирующего контура в соответствии с [1] определяется выражением:
.
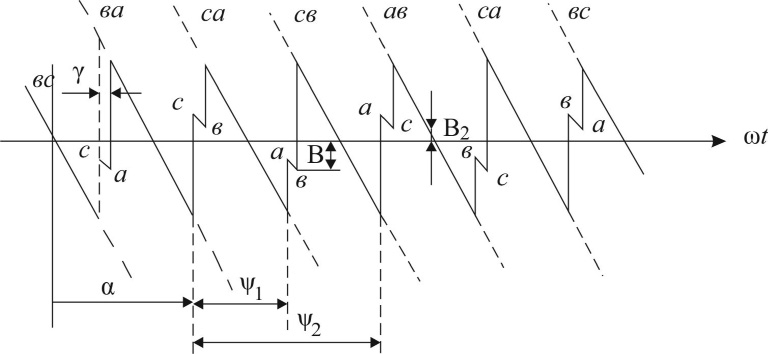
Рис. 2. Диаграмма напряжения на нагрузке в трехфазном мостовом ТП при α ≈ 90°
Из этого выражения видно, что Lγ зависит от значения угла Ψ. В процессе одной коммутации Lγ не остается постоянной величиной и, следовательно, в соответствии с [1] меняется темп изменения токов 
и 
. Строго говоря, в коммутации участвуют две фазы одновременно, но на первом этапе влияние фазы, имеющей сдвиг Ψ2 = 120°, незначительно по сравнению с быстродействующей фазой. Здесь ub максимально отстоит от нулевой линии. На втором этапе влияние этой фазы уже завершается и процесс коммутации определяется «медленнодействующей» фазой. Величина ub становится ближе к нулевому значению.
По диаграмме напряжения на нагрузке определяется значение ub. Для этого используются бóльшие отклонения от среднего значения напряжения, имеющие место при Ψ1 = 60°. Для удобства измерения мгновенного напряжения на экране осциллографа, изменив развертку изображения во времени, совмещают четные и нечетные импульсы пульсаций [1] (рис. 3).
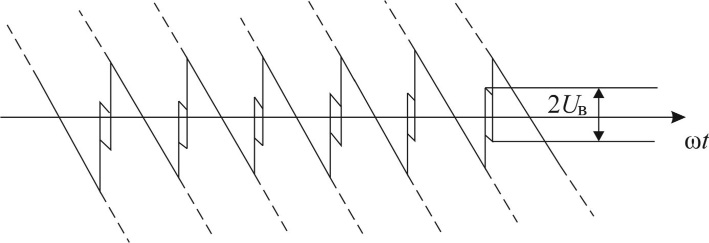
Рис. 3. Диаграмма напряжения при совмещении четных и нечетных импульсов пульсаций
Измерив величину 2ub, определяется в вольтах значение ub. По значениям u2 и ub определяется Nkγ. В работе [1] получены уравнения, в которых содержится параметр Nkγ. Для его определения решается одно из этих уравнений относительно Nkγ. Получаем:
(*)
При 
и 
формула (*) упрощается:
Для трехфазной мостовой схемы тиристорного преобразователя 
, 
, и выражения становятся еще проще:
Вторичное индуктивное сопротивление питающего трансформатора определяется по формуле:
Следующий этап – теоретическое исследование изолированной системы электропривода. Исходя из каталожных данных питающего трансформатора, определяется индуктивное сопротивление короткого замыкания трансформатора χkТР. Затем определяется индуктивное сопротивление коммутирующего контура для трансформатора, питающегося от сети бесконечно большой мощности:
Здесь величина NγТР определена из формулы:
Откуда:
Заключение
Таким образом, определены значения первичного и вторичного индуктивных сопротивлений рассеяния питающего трансформатора, от которых зависит выбор правильного соотношения мощностей электропривода.
Рецензенты:Казанцев В.П., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 18.04.2014.