Определение силового взаимодействия между размольными ферроэлементами цилиндрической формы сводится к задаче определения сил и моментов, действующих на систему намагниченных стержней, размещенных в магнитном поле рабочего объема электромагнитного механоактиватора (ЭММА) [1–6]. При внесении стержней в невозмущенное магнитное поле происходит искривление магнитных силовых линий, их преломление на границах стержней. В результате возникает напряженное состояние поля, которое проявляется в силовом воздействии на стержень. Поэтому задача об определении сил и моментов, действующих на стержень со стороны деформированного магнитного поля в рабочем объеме ЭММА цилиндрических конструкций [7–11], распадается на две задачи:
1. Определение деформированного магнитного поля.
2. Определение сил и моментов, действующих на стержень со стороны поля.
Первая задача решается независимо от второй. В статье представлены результаты решения задачи определения деформированного магнитного поля в рабочем объеме ЭММА цилиндрических конструкций с магнитоожиженным слоем размольных ферротел цилиндрической формы.
Целью данной работы является решение задачи определения деформированного магнитного поля в рабочем объеме электромагнитных механоактиваторов цилиндрических конструкций с магнитоожиженным слоем размольных ферротел цилиндрической формы.
Материал и методы исследований
Предметом исследований является магнитное поле в рабочем объеме электромагнитных механоактиваторов, деформированное магнитоожиженным слоем ферротел цилиндрической формы.
Результаты исследования и их обсуждение
Приняты следующие основные положения: стержни (размольные ферроэлементы) имеют одинаковую цилиндрическую форму с окружностью радиуса r = 1 в сечении; оси стержней параллельны; cтержни изготовлены из одного и того же намагничиваемого материала с магнитной проницаемостью μ и пренебрежимо малой коэрцитивной силой; cтержни находятся во внешнем магнитном поле, вектор напряжеyности которого ортогонален осям стержней; вектор напряженности невозмущенного поля параллелен оси OY.
Исследования выполнены в абсолютной системе координат, ось которой направлена параллельно осям стержней. Индукция невозмущенного магнитного поля имеет вид В = (В0, 0, 0). Картина возмущенного магнитного поля будет одна и та же в плоскостях, параллельных плоскости OXY. В рассматриваемом случае векторный магнитный потенциал имеет всего лишь одну, отличную от нуля, компоненту Аz: A = (0, 0, Az). Зная векторный магнитный потенциал, определяемый из выражения 
можно найти индукцию магнитного поля В в любой точке рабочего объема ЭММА. При этом векторный магнитный потенциал и все его компоненты в области, не занятой точками, гармоничен, т.е. удовлетворяет уравнению Лапласа
ΔAz = 0, (1)
где Δ – оператор Лапласа.
Будем искать решение уравнения (1) в виде суммы потенциалов простых слоев с неизвестными плотностями
(2)
где n – число стержней; Сi – сечение i-го стержня плоскостью z = 0; Р – точка плоскости XOY; Ω – точка, лежащая на Сi; Ri (P,Ω) – расстояние между точками Р и Ω; σi(Ω) – плотность i-го простого слоя; В0х – потенциал невозмущенного магнитного поля.
Если А = (0,0, – В0 х), то В = rot A = (0, B0, 0). Намагничиваемые стержни заменяем токовыми слоями с плотностями σi(Ω) [1].
Рассмотрим поведение магнитного поля вблизи границы k-го стержня. Для этого перепишем формулу (1), выделив потенциал k-го стержня
(3)
где 
(4)
В дальнейшем будем полагать В0 = 1.
Известно, что на границе двух сред с различными магнитными проницаемостями остаются непрерывными нормальная составляющая магнитной индукции и касательная составляющая напряженности магнитного поля [12].
Выражение для вектора В в цилиндрической системе координат имеет вид
(5)
где n, τ и k – орты системы координат.
Поэтому 
, Bz = 0.
Рассмотрим систему координат с центром, совпадающим с центром сечения k-го стержня. Тогда точки, принадлежащие сечению k-го стержня, будут иметь координаты (cos φ, sin φ), а точки, принадлежащие сечению i-го стержня (i ≠ k), будут иметь координаты (Pik cos αi + cos ψi, Pik sin αi + sin ψi), где Pik и αi – координаты центра сечения стержня.
Направления нормали в точках сечения k-го стержня совпадают с его радиусом
(6)
Подставляя в эту формулу выражение (4), найдем
(7)
где 
(8)
Зафиксируем в формуле (8) угол φ и будем приближать r к единице (радиус k-го сечения) снаружи стержня и изнутри. При этом, как известно [12], нормальная производная простого слоя терпит разрыв. Обозначим через Bτe и Bτi пределы, к которым стремится Вτ при стремлении r к единице снаружи и изнутри. Получим [12]
(9)
(10)
Нетрудно показать, что
Из рисунка а следует, что
Известно [12], что 
. Следовательно, из формул (9) и (10) получим
(11)
(12)
а б
К решению интегральных уравнений относительно неизвестных функций: а – стержень в рабочем объеме ЭММА; б – два стержня в рабочем объеме ЭММА
Касательная составляющая напряженности магнитного поля на границе k-го стержня остается непрерывной. Следовательно,
(13)
Подставляя в выражение (13) формулы (11) и (12), найдем
(14)
или в развернутом виде
(15)
где k = 1, …, n.
Система (15) является системой линейных интегральных уравнений относительно неизвестных функций σi(φ).
Для решения системы линейных интегральных уравнений (15) попытаемся аппроксимировать ядра этой системы вырожденными. Напомним, что ядро называется вырожденным, если оно представимо в виде суммы произведений функций, каждая из которых зависит только от одной переменной.
Как и раньше, поместим начало координат в центр сечения k-го стержня. Тогда координаты точек, лежащих на окружности сечения k-го стержня, будут
(rK cosφK, rK inφK). (16)
Координаты точек, лежащих на окружности сечения j-го стержня, имеют вид
(17)
где СKi – расстояние между центрами сечений k-го и j-го стержней; αKj – угол, показанный на рисунке б.
Расстояние RKj между точками, лежащими на окружностях сечений k-го и i-го стержней, имеет вид
(18)
где 
(19)
Для ядра Kij имеем следующее выражение:
(20)
Для параметра Eij имеем следующую очевидную оценку:
0 ˂ Eij ≤ 1/2. (21)
Разложим ядро Kij в ряд по степеням параметра Eij
(22)
Ввиду соотношения
(23)
интерес представляет только третье слагаемое в формуле (22), которое обозначим через 
(24)
Система линейных интегральных уравнений (15) теперь может быть переписана в следующем виде
(25)
EKi = EiK; 
, αKi = π + αiK,
где k = 1,…, n4.
Систему (25) необходимо дополнить следующими соотношениями
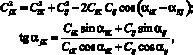
где i = 1,…, n; j = 1,…, n.
Заключение
В результате найдены неизвестные плотности простых слоев σi(φ) (i = 1,…n) и определен потенциал Az(P) для любой точки Р плоскости, перпендикулярной осям стержней, что позволяет определить деформированное магнитное поле и решить задачу определения сил и моментов, действующих на ферромагнитные размольные элементы в рабочем объеме ЭММА цилиндрических конструкций при различных коэффициентах его объемного заполнения ферромагнитной составляющей.