Настоящая работа основана на материале, представленном в [1]. Приведём его краткое изложение.
К числу классических в теории принятия решения относится многокритериальная задача линейного программирования (МЛП), формальная постановка которой имеет вид:
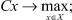(1)
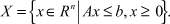(2)
Здесь, в отличие от обычной задачи линейного программирования (ЛП), С – матрица размерности l×n, а не вектор. А – матрица ограничений размерности m×n. Таким образом, многокритериальная задача (1), (2) предполагает максимизацию на многограннике X не одного линейного критерия, как в обычной задаче (ЛП), а l-критериев одновременно.
Заметим, что от нормальной формы задачи (1), (2) легко можно перейти к канонической. Ограничение х ≥ 0 также легко обходится.
Как правило, традиционного решения задачи (1), (2) не существует, то есть отсутствует точка x ∈X такая, что Cx ≥ Cy для всех y ∈ X, y ∈ x. В случае, когда у лица, принимающего решение (ЛПР), отсутствует какая-либо априорная информация относительно сравнительной важности критериев, под решением задачи (1), (2) будем понимать множество Парето. Обозначим его через N ∈ X. Решение x ∈ N называется паретовским (недоминируемым, неулучшаемым), если его нельзя улучшить по какому-то одному критерию, не ухудшив значение хотя бы одного из оставшихся. Или, формально,
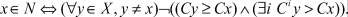
Проблеме построения множества Парето в задаче МЛП посвящена обширная литература. Вместе с тем одной из лучших (если не лучшей) публикацией на эту тему является, по-видимому, статья американских математиков P.L. Yu и M. Zeleny [8]. Именно здесь приведены хорошо теоретически обоснованные методы построения множества паретовских вершин Nex ∈ N и всего множества Парето.
Для построения множества Nex в [8] представлен так называемый многокритериальный симплекс-метод. Он основан на двух основных теоремах, формулировки которых мы приведем здесь без доказательства.
Теорема 1 ([8]). Множество Ne связно.
Теорема 2 ([8]).
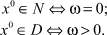
Здесь D = X/N, а ω – решение задачи ЛП
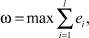(3)
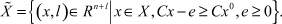(4)
Суть алгоритма построения множества Nex, описанного в [8], состоит в следующем. Сначала ищется первая паретовская вершина x1. Для этого достаточно решить задачу ЛП с целевой функцией
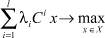, λ > 0.
После этого на паретовость путем решения задачи (3), (4) проверяются все соседние к x1 точки. Те из них, которые окажутся паретовскими, включаются в Nex, проверке подвергаются соседние к ним и т.д.
Следует отметить, что в [8] приведен (см. например, теорему 3.1 в [8]) ряд простых достаточных условий принадлежности некоторой произвольной точки y ∈ X множеству D, что существенно облегчает перебор.
Наряду с многокритериальным симплекс-методом в [8] показано, что для любой точки x ∈ Nex существует набор чисел λi ∈ (0, 1),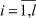 
такой, что
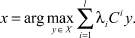(5)
Это означает, что множество Nex можно построить, перебирая узлы l – мерной Σ-сети на множестве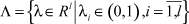 
и решая для каждого узла задачу ЛП (5).
Далее в [2] показывается, как на основе Nex можно построить множество N. При этом N будет представлять собой объединение паретовских выпуклых комбинаций (граней многогранника X) точек из Nex.
Заметим, что со всем множеством Парето N работать трудно, поскольку оно содержит бесконечное число возможных «равноправных» решений, ЛПР же, как правило, для реализации требуется какое-то одно решение. В то же время вся объективная информация уже использована как будто бы при построении множеств Nex и N.
Казалось бы, выходом из этой ситуации может быть решение задачи ЛП(5) с равными весовыми коэффициентами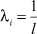 
. Это, однако, не так по двум причинам. Во-первых, такой способ предполагает одинаковую важность для ЛПР всех l критериев, что сужает постановку исходной задачи. И, во-вторых, такое решение непременно «выведет» на какую-нибудь точку из Nex (то есть на вершину), игнорируя, по существу, множество N/Nex.
Способ, позволяющий ЛПР выделить для реализации лишь одну точку из N и не требующий дополнительных соображений субъективного характера, может состоять в следующем. Заметим, что впервые он изложен в [8], в настоящей же работе произведено его уточнение и развитие.
Прежде всего заметим, что каждое паретовское решение x ∈ N равноправно по отношению к другим паретовским решениям (не лучше, но и не хуже них). Следовательно, при выделении единственной точки из N (то есть при точечной характеризации N) для реализации должно быть учтено (пусть и неявно) все множество N.
Отметим далее, что такая характеризация – обозначим ее через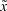 
– должна отражать конфигурацию множества N, в значительной мере задаваемую множеством Nex.
Основанная на учете этих двух соображений идея поиска решения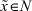 
состоит в следующем. Необходимо, считая каждую точку из Nex равноправной по отношению к другим, найти выпуклую комбинацию всех точек из Nex с равными весами. Обозначим её через x*:
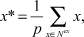(6)
где p – число элементов (мощность) множества Nex.
Ясно, что в общем случае точка x* не является паретовской. Поэтому естественно в множестве N выделить точку (ранее обозначенную через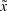 
), в максимальной степени «улучшающую» x* по всем критериям.
Воспользуемся для этого теоремой 2 и решим задачу (3) на множестве
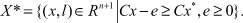(7)
А теперь, основываясь на этом материале, поставим ряд интересных, подлежащих решению вопросов, связанных с интервально заданными исходными данными. То есть будем предполагать, что эти данные заданы не точечно, а интервально следующим образом:
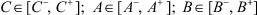
При этом будем считать, что любая информация, уточняющая расположение компонент указанных вектора и матриц, отсутствует. Некоторые приёмы оперирования интервальными данными представлены в работах [2–7].
Итак, эти вопросы можно сформулировать следующим образом. Является ли такая постановка корректной в принципе? Если да, то что понимать в этом случае под множеством Парето и как будет «работать» многокритериальный симплекс-метод? Что тогда следует понимать под «компромиссным решением»? Может быть, то же множество, как в большинстве интервальных задач?
Решению этих и смежных вопросов авторы намерены посвятить свои последующие работы.
При этом необходимо иметь в виду следующее. Центральной проблемой, связанной с решением многокритериальной линейной задачи в интервальной постановке, является классическая для интервального анализа проблема отыскания решения интервальной системы линейных алгебраических уравнений (ИСЛАУ – принятая в интервальном анализе аббревиатура)
Az = B,
где А – интервальная вещественная матрица размерности (n×m); B – n-мерный интервальный вектор, элементами которых являются соответственно интервалы и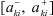 
, 
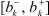, z Є Rm. Множество решений ИСЛАУ может быть определено различными способами в зависимости от того, какими кванторами связаны коэффициенты матрицы и правой части. Наиболее часто в литературе встречаются следующие множества решений, подробно описанные в работах У. Оэттли, У. Прагера, И. Рона, А.В. Лакеева, С.И. Носкова, С.П. Шарого:
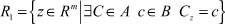– объединенное множество решений ;
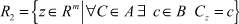– допустимое множество решений ;
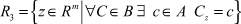– множество впервые рассмотренной при решении интервальной задачи модельного управления;
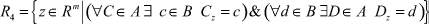– множество всех точечных алгебраических интервальных решений.
Множества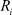 
, 
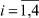представимы также в виде
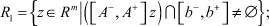
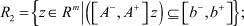
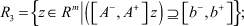
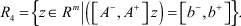
Здесь A–, A+ и b–, b+ – матрицы и вектора, состоящие из элементов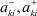 
и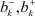 
, 
, 
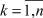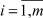соответственно.
Очевидны следующие соотношения между Ri,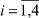 
:
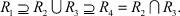
В работах указанных авторов показано, что множества решений ИСЛАУ представимы в виде:
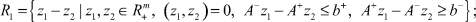
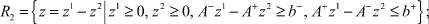
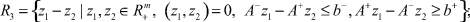
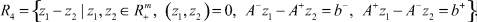
Анализ описаний Ri,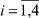 
показывает, что лишь множество R2 (допустимое множество решений ИСЛАУ) представляет собой область совместности системы линейных неравенств. Остальные множества R1, R3, R4 описываются системами линейных неравенств и нелинейным условием (z1, z2) = 0, которое сильно затрудняет работу с этими множествами. От него можно избавиться посредством расширения размерности задачи введением булевых переменных σi, 
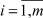по правилу:
0 ≤ z1i ≤ σiM;
0 ≤ z2i ≤ (1 – σi)M; σi = 0,1,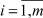 
,
где М – заранее выбранное большое положительное число.
После введения таких переменных для работы с множествами R1, R3, R4, в частности, решения на них различных оптимизационных задач, можно воспользоваться программными средствами решения задач частично-целочисленного линейного программирования.
Нетрудно также показать обратное, а именно то, что любую задачу булевого программирования можно заменой переменных свести к задаче с условиями типа z1 ≥ 0, z2 ≥ 0, (z1, z2) = 0. Действительно, рассмотрим задачу булевого программирования
Aσ ≤ b
σi = 0,1,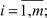 
(c, σ) → max.
Тогда, введя вещественные переменные z1i, z2i,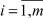 
по правилу
σ = z1 + z2;
0 ≤ z1 ≤ 1, 0 ≤ z2 ≤ 1,
(z1, z2) = 0,
получим эквивалентную постановку
A(z1, z2) ≤ b;
0 ≤ z1 ≤ 1, 0 ≤ z2 ≤ 1;
(z1, z2) = 0;
(c, z1 + z2) → max.
Рецензенты:
Кузьмин О.В., д.ф.-м.н., профессор, заведующий кафедрой теории вероятностей и дискретной математики Иркутского государственного университета, г. Иркутск;
Лакеев А.В., д.ф.-м.н., ведущий научный сотрудник ИДСТУ СО РАН, г. Иркутск.
Работа поступила в редакцию 11.04.2014.