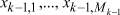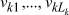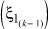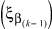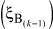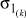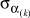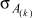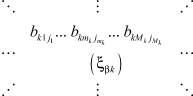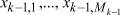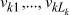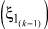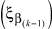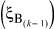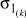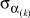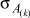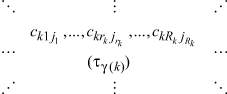Сложные дискретные клеточно-иерархические системы характеризуются многостадийностью процесса превращения сырья и исходных материалов в готовую продукцию. Основной задачей структурного клеточно-иерархического моделирования таких систем является построение структурных схем автоматов на основе их композиции. Для клеточно-иерархического синтеза сложных многостадийных дискретных систем используются итеративные цепи, базирующиеся на клеточной интерпретации. Моделируется иерархическая упорядоченная последовательность автоматов, описывающих систему как совокупность взаимосвязанных объектов (стадий обработки, агрегатов, операций). При синтезе достаточно сложных автоматов, соответствующих отдельным стадиям обработки, их разбивают на отдельные клетки (элементарные автоматы), формирующие внутренние итеративные цепи.
Определение 1. Итеративная цепь – композиция неоднородных клеток (автоматов) разной степени сложности, имеющих последовательное соединение, в которых внутренние выходы предыдущих клеток (автоматов) являются внутренними входами последующих.
Определение 2. Дискретная клеточно-иерархическая система – система многоуровневой структуры, представляющая собой композицию сложных автоматов (клеток), которые разбиваются на отдельные клетки (элементарные автоматы), формирующие внутренние итеративные цепи.
Процесс структурного моделирования начинается с формирования функциональных блоков, соответствующих отдельным стадиям обработки, каждый из которых представляется в виде конечного автомата высокого уровня. Каждая операция, соответствующая определенной стадии обработки, может быть описана в виде клетки без памяти и является автоматом нижнего уровня. Так как операции выполняются на отдельных технологических агрегатах, то каждый из агрегатов, в свою очередь, описывается в виде автомата более высокого уровня (автомата агрегата), который включает в себя цепочку клеток, образованную автоматами операций. Данная цепочка формирует линейную итеративную цепь [1, 2].
Аналогично, на более высоком уровне стадии обработки объединяют группы технологических агрегатов и могут быть представлены в виде комбинации клеток (автоматов стадий обработки), включающих в себя цепочки клеток (автоматов агрегатов) в виде внутренних итеративных цепей. После моделирования внутренних цепей иерархии клеток определяются внутренние входы и выходы каждой клетки всех уровней.
Сложные промышленные системы имеют структуру, дискретную по времени, пространству и алфавитам. Они обладают сложной нелинейной структурой связей по входам, состояниям и выходам, алфавиты которых конечны. По стадиям обработки формируются функциональные блоки, которые описываются автоматами. При синтезе достаточно сложных автоматов их разбивают на отдельные клетки (элементарные автоматы), формирующие итеративные цепи или сети. Таким образом, в общем случае производственный процесс можно представить в виде композиции автоматов. В полученной системе производится отождествление стадий обработки с отдельными автоматами.
На следующем этапе формулируются условия работы каждого автомата, т.е. определяются условия его взаимодействия с другими объектами, выявляются необходимые входы и выходы автомата и намечается общий закон появления выходных сигналов в зависимости от воздействия на входы автомата. Упорядоченная последовательность автоматов, входящих в систему, которая характеризуется тем, что хотя бы один из выходных узлов каждого предыдущего автомата соединен с некоторым входным узлом следующего за ним автомата, формирует итеративную цепь.
При моделировании сложных автоматов их разбивают на отдельные клетки (элементарные автоматы), формирующие итеративные цепи или сети [1-3]. Цепи являются итеративными, т.к. процесс определения параметров каждой клетки связан с производственным процессом. По мере продвижения полуфабриката по стадиям обработки фиксируются значения технологических факторов, которые поступают в автоматы, соответствующие определенным стадиям обработки. Отсюда сигналы, вырабатываемые автоматами цепи, зависят от сигналов автоматов (клеток), сформированных на предыдущих стадиях обработки (итерациях).
Для каждой клетки необходимо формировать свои законы изменения состояний и выходов, описываемые в виде уравнений или таблиц. Отсюда можно сформировать таблицы переходов и выходов для каждой клетки (табл. 1, 2).
Таблица 1
Таблица переходов для k-й стадии обработки (k-й клетки цепи)
|
|
|
… |
|
… |
|
|
…
…
|
|
||||
Алфавиты входов, состояний и выходов могут иметь разную значность, и их составляющие представляются (кодируются) следующим образом:
k = 1, ..., K – номер стадии обработки (агрегата), 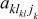 – составляющая алфавитов входов, где
– составляющая алфавитов входов, где 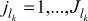 , где
, где 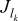 – значность алфавита l-го входа на k-м агрегате, lk = 1, ..., Lk – номер входа (элементов сырья, полуфабрикатов) на k-м агрегате,
– значность алфавита l-го входа на k-м агрегате, lk = 1, ..., Lk – номер входа (элементов сырья, полуфабрикатов) на k-м агрегате, 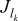 – значность алфавита l-го входа на k-м агрегате,
– значность алфавита l-го входа на k-м агрегате, 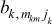 – составляющая алфавитов состояний (технологических факторов) для k-го агрегата,
– составляющая алфавитов состояний (технологических факторов) для k-го агрегата, 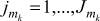 , где
, где 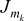 – значность алфавита m-го технологического фактора на k-м агрегате, mk = 1, ..., Mk – номера факторов на k-й стадии обработки.
– значность алфавита m-го технологического фактора на k-м агрегате, mk = 1, ..., Mk – номера факторов на k-й стадии обработки. 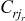 – составляющая алфавитов r-го выхода, jk = 1, ..., Jk – значность алфавита p-го выхода, r = 1, ..., R – номер выхода.
– составляющая алфавитов r-го выхода, jk = 1, ..., Jk – значность алфавита p-го выхода, r = 1, ..., R – номер выхода.
Таблица 2
Таблица выходов для k-й стадии обработки (k-й клетки цепи)
|
|
|
… |
|
… |
|
|
…
…
|
|
||||
Таким образом, конечный входной алфавит:
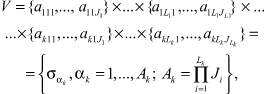 (1)
(1)
где σα – вариант сочетаний алфавитов входов V[t]; Ak – максимальное количество сочетаний алфавитов входов на k-м агрегате.
Конечный внутренний алфавит (алфавит технологических факторов)
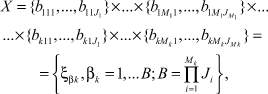 (2)
(2)
где 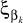 – вариант сочетания алфавитов на k-м агрегате; K – число агрегатов; mk – число факторов на k-м агрегате.
– вариант сочетания алфавитов на k-м агрегате; K – число агрегатов; mk – число факторов на k-м агрегате.
Вариант сочетания алфавитов на 1-м агрегате:
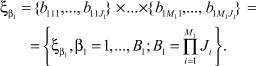 (3)
(3)
Вариант сочетания алфавитов на k-м агрегате:
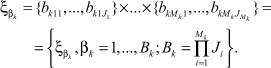 (4)
(4)
Вариант сочетания алфавитов на последнем агрегате:
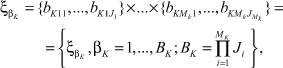 (5)
(5)
где σα – вариант сочетания алфавитов V[t] на всех агрегатах:
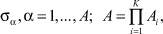 (6)
(6)
где ξβ – вариант сочетания алфавитов x[t] на всех агрегатах:
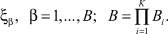 (7)
(7)
Конечный выходной алфавит:
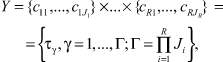 (8)
(8)
где τγ – вариант сочетания алфавитов входов y[t].
Автоматы, для которых функции переходов и выходов определены на всех парах входов и состояний, являются полностью определенными или полными автоматами. Автоматы, для которых функции переходов и выходов определены не на всех парах входов и состояний, являются недоопределенными автоматами. Неиспользуемые пары в таблицы не заносятся.
Функция выходов имеет вид:
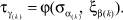 (9)
(9)
Сочетание алфавитов состояний на входе k-й клетки цепи, описывающей многостадийную пространственно-распределенную систему, 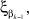
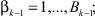
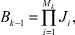 представленное в таблице переходов, в результате операции перехода всегда будет попадать в один и тот же блок сочетания алфавитов состояний на выходе k-й клетки цепи
представленное в таблице переходов, в результате операции перехода всегда будет попадать в один и тот же блок сочетания алфавитов состояний на выходе k-й клетки цепи 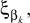
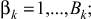
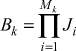 .
.
Теорема 1. Для того, чтобы два варианта сочетания алфавитов состояний k-й клетки цепи, описывающей многостадийную пространственно-распределенную систему, (ξi(k)) и (ξj(k)) были эквивалентны и итеративная цепь не различала их, необходимо и достаточно, чтобы под воздействием варианта сочетаний алфавитов входов 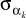 цепь переходила в одинаковое сочетание алфавитов выходов
цепь переходила в одинаковое сочетание алфавитов выходов 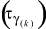 .
.
Доказательство.
(Необходимость). Нужно доказать, что варианты сочетаний алфавитов состояний k-й клетки цепи эквивалентны:
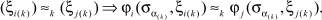
Доказательство от противного. Если функции выходов 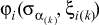 и
и 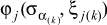 различны и
различны и 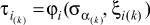 и
и 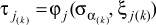 , то
, то 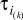 и
и 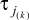 могут различаться, а следовательно, итеративная цепь будет различать их и
могут различаться, а следовательно, итеративная цепь будет различать их и 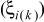 ,
, 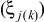 не эквивалентны.
не эквивалентны.
(Достаточность). Нужно доказать, что
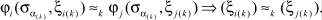
Если для варианта сочетаний алфавитов входов 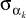 ,
, 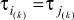 , то
, то 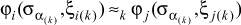 . Следовательно,
. Следовательно, 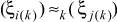 .
.
Теорема 2. Если итеративная цепь, соответствующая многостадийной пространственно-распределенной системе, состоит из конечной конфигурации автоматов с заданным конечным набором сочетаний алфавитов состояний, функции переходов которых описываются в табличной форме, то для любого автомата может быть сформирована последовательная декомпозиция элементарных автоматов.
Доказательство.
Поскольку задана таблица переходов, содержащая конечное множество возможных сочетаний алфавитов состояний, то соответствующие сочетания k-й клетки цепи могут быть описаны как функция определенных сочетаний предыдущих клеток, которые могут быть объединены в одну клетку, что и определяет последовательную декомпозицию элементарных автоматов. Данные выводы подтверждаются работами [2–7].
Конечный автомат, описывающий многостадийную пространственно-распределенную систему, моделируется внутренними цепями иерархии клеток, в которых аргумент времени t не является основополагающим и заменяется на пространственный аргумент s.
Любой автомат цепи i-го уровня, соответствующий многостадийной пространственно-распределенной системе, всегда может быть смоделирован в виде итеративной цепи i + 1-го уровня, вход которой является входом автомата X[s – 1]i, а выход – выходом автомата X[s1]i.
Заключение
Разработана методология структурного моделирования дискретных клеточно-иерархических систем. Выявлены структурные элементы таких систем, определены их основные характеристики. Доказаны теоремы об использовании внутренних цепей иерархии клеток и автоматных подходов, описывающие правила моделирования дискретных клеточно-иерархических систем.
Рецензенты:
Володин И.М., д.т.н., профессор, проректор по научной работе, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк;
Шмырин А.М., д.т.н., доцент, заведующий кафедрой высшей математики, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк.
Работа поступила в редакцию 11.04.2014.