В практике обогащения твердых сыпучих полезных ископаемых наиболее частое применение находят наклонные вибрационные грохоты. Одним из наиболее важных показателей работы грохота является его эффективность, которая при правильно подобранных параметрах может достигать 97 % [4]. Для достижения таких результатов необходимы серьезные затраты, так как эффективность грохочения в большинстве случаев определяется опытным путем, а теоретические методики ее определения являются приближенными.
На эффективность работы грохота влияет множество различных факторов, таких как угол наклона рабочего органа, форма отверстий сита, высота подачи материала и др. Этими факторами определяется вероятность прохождения частиц сквозь решетку грохота. Очевидным является тот факт, что процесс классификации горных пород по крупности носит вероятностный характер.
Большинство работ по определению вероятности просеивания было проведено с идеализированной частицей, имеющей сферическую форму, которая просеивалась через сита с квадратными отверстиями [6].
Как отмечалось ранее, конструктивное исполнение просеивающей поверхности грохота влияет на вероятность прохождения частиц сквозь нее.
В свою очередь, просеивающие поверхности характеризуются таким параметром, как коэффициент живого сечения L, равный отношению площади отверстий сетки в свету к ее общей площади, выраженное в процентах или в долях единицы [5].
Если бы рудные частицы бросали на решетку грохота по одной, то наилучшим расположением плоскости решетки для мелких частиц было бы горизонтальное, так как площадь «живого сечения» ячейки в данном случае максимальная, а потому вероятность прохождения мелкой частицы через ячейку наибольшая.
При увеличении угла наклона сита уменьшается кажущаяся величина отверстий сита, равная величине проекции действительного отверстия на горизонтальную плоскость
dk = cos α, (1)
где dk – кажущаяся величина отверстий сита; d – действительная величина отверстий сита, мм %; α – угол наклона сита к горизонту.
Теоретически эффективность грохочения можно определить как вероятность прохождения частиц сквозь решетку грохота. Эта величина зависит от количества ударов частиц об решетку грохота перед их просеиванием. Так, при однократном прохождении материала сквозь решетку грохота вероятность прохождения сквозь решетку грохота ε1 равна
ε1 = Lcos φ, (2)
где L – коэффициент живого сечения просеивающей поверхности, равный отношению площади отверстий к общей площади сетки; φ – угол наклона рабочей поверхности грохота.
Часть материала, количественно равная (1 – L), отразится от прутков решетки и вновь упадет на сетку. Из этой части пройдет сквозь сетку следующая величина, равная
ε2 = ((1 – L)L)cos φ, (3)
а часть (1 – L)2 отразится.
В результате суммарная вероятность прохождения частиц сквозь решетку грохота определится как
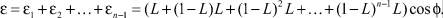 (4)
(4)
Выражение (4) может быть преобразовано по формуле суммы геометрической прогрессии к следующему виду
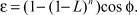 (5)
(5)
В зависимости от количества ударов о сетку теоретическая эффективность грохочения увеличивается и в пределе стремится к 100 %.
Рассмотрим пример по определению теоретической эффективности с ситом, коэффициент живого сечения которого равен 66 %. Эта эффективность для данного сита при угле его наклона в 20 градусов была рассчитана по формуле (5) и на основе полученных результатов построен график зависимости теоретической эффективности от количества ударов (рис. 1).
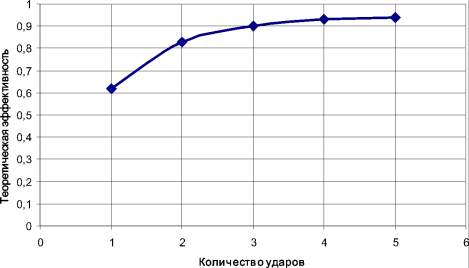
Рис. 1. Зависимость теоретической эффективности от количества ударов
Анализируя зависимость, представленную на рис. 1, заметим, что теоретическая эффективность растет от удара к удару и стремится к 100 %. Очевидно, что чем больше ударов совершит частица, тем выше будет вероятность ее просеивания.
Таким образом, необходимо так подобрать конструктивные и режимные параметры грохота с учетом упругих и фрикционных характеристик горных пород [3], чтобы количество возможных ударов о плоскость сетки было как можно больше.
Для определения необходимой величины количества ударов частиц необходимо установить кинематические параметры движения частиц на поверхности грохота, ограниченной длиной рабочей поверхности.
При попадании рудных частиц в рабочее пространство грохота возможно два варианта развития событий:
1 вариант. Удар частицы о пруток сетки.
2 вариант. Просеивание сквозь ячейки сетки.
Для исследования влияния входных параметров установки (угла наклона рабочей поверхности φ и высоты подачи материала h) составлена математическая модель, включающая уравнения свободного полета частиц и их удара о наклонную плоскость [2].
Частицы падают на поверхность грохота вертикально, поэтому в момент соприкосновения с наклонной плоскостью вектор скорости падения V0 составляет угол φ с нормалью к этой плоскости.
Величину скорости после удара Ui и угол отражения βi при произвольном ударе «i» находим из системы уравнений, определяющих коэффициент восстановления и коэффициент трения при ударе [1], а также из уравнений теоремы об изменении количества движения
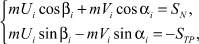 (6)
(6)
где m – масса частицы; Ui – скорость после удара, м/с; βi – угол отражения при произвольном ударе, град.; Vi – скорость перед ударом, м/с; αi – угол падения при произвольном ударе, град.; SN – импульс нормальной реакции при ударе; SТР – импульс силы трения.
Угол отражения
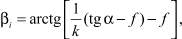 (7)
(7)
где f – коэффициент трения при ударе; k – коэффициент восстановления.
Величина скорости после удара может быть определена по формуле:
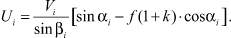 (8)
(8)
После отражения частицы от поверхности грохота происходит ее свободный полет, схема которого показана на рис. 2.
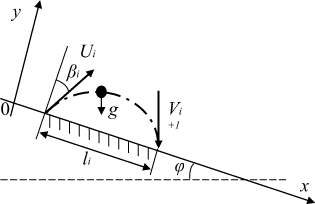
Рис. 2. Расчетная схема движения частиц на наклонной плоскости
Если пренебречь силами сопротивления движению частицы, то уравнения ее движения в свободном полете можно получить из соотношений кинематики равнопеременного движения. Так как ax = gsin φ, ay = –gcos φ, то в системе координат, связанной с поверхностью грохота, эти уравнения имеют вид
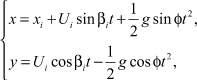 (9)
(9)
где xi – координата положения частицы на наклонной плоскости, м; t – текущее время.
Из второго уравнения системы (9) при условии, что у = 0, выразим текущее время
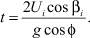 (10)
(10)
Дальность полета li вдоль поверхности грохота до следующего удара находим, исключив из системы уравнений (9) параметр текущего времени
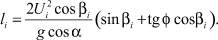 (11)
(11)
По данным кинематическим параметрам, учитывающим не только входные и режимные параметры, но и фрикционные и упругие характеристики горных пород, довольно точно можно спрогнозировать количество их отражений.
Рецензенты:
Герц Э.Ф., д.т.н., профессор, декан лесоинженерного факультета, ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург;
Готлиб Б.М., д.т.н., профессор, заведующий кафедрой «Мехатроника», ФГБОУ ВПО «Уральский государственный университет путей сообщения», г. Екатеринбург.
Работа поступила в редакцию 11.04.2014.



