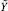Рентабельность от реализации мёда является основным показателем деятельности сельскохозяйственной организации, производящей пчеловодческую продукцию. В связи с этим в нашей работе ставится задача определения основных факторов, воздействующих на рентабельность от продажи мёда по совокупности сельскохозяйственных организаций Республики Башкортостан.
Произведем корреляционно-регрессионный анализ на основе данных за 2004–2012 гг. по следующей схеме:
1) определяем факторы, которые оказывают воздействие на изучаемый показатель, и отберем наиболее существенный из них;
2) собираем исходную информацию по каждому из факторных и результативному признаков;
3) смоделируем связь между факторами и результативным показателем, т.е. подберем и обоснуем математическое уравнение, которое будет наиболее точно выражать сущность исследуемой зависимости;
4) произведем расчет основных показателей связи корреляционно-регрессионного анализа: уравнение связи, коэффициент корреляции, детерминации, эластичности и т.д.;
5) статистически оценим результаты корреляционно-регрессионного анализа и дадим рекомендации для дальнейшего развития результативного показателя.
Результаты исследований и их обсуждение
В рамках первого этапа определяется перечень показателей, которые предлагается включить в модель. В качестве зависимой переменной (результативного показателя) Y принимается рентабельность от реализации мёда (отношение прибыли от реализации мёда к полной себестоимости реализованного мёда), приведенный в процентах. Независимыми, объясняющими показателями (факторами) X являются следующие:
Х1 – затраты на одну пчелосемью (отношение всех затрат на производство продукции пчеловодства к численности пчелосемей), руб;
Х2 – продуктивность пчелосемей (выход мёда на одну пчелосемью – отношение валового мёда к численности пчелосемей), кг;
Х3 – себестоимость 1 ц мёда (отношение себестоимости всего мёда к объему произведенного мёда), руб.;
Х4 – цена реализации 1 ц мёда (отношение выручки от реализации мёда к объему реализации мёда), руб.;
Х5 – уровень товарности (отношение реализованного объема мёда к произведенному объему мёда), %.
Исходная информация для проведения экономико-математического моделирования рентабельности реализации мёда по сельскохозяйственным организациям Республики Башкортостан приведена в табл. 1.
Сравнительная оценка и отбор факторов осуществляется на основе анализа парных коэффициентов корреляции и оценки их значимости.
Таблица 1
Исходная информация для экономико-математического моделирования рентабельности реализации мёда по сельскохозяйственным предприятиям Республики Башкортостан за 2004–2012 гг.
|
Годы |
Рентабельность, % |
Затраты на на 1 пчелосемью, руб. |
Мёдопродуктивность пчелосемей, кг |
Себестоимость 1 ц мёда, руб. |
Цена реализации 1 ц мёда, руб. |
Уровень товарности, % |
|
У |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
|
|
2004 г. |
39,7 |
1513 |
26,6 |
6938 |
9691 |
30,4 |
|
2005 г. |
33,7 |
1540 |
23,4 |
6758 |
9036 |
33,3 |
|
2006 г. |
29,5 |
1687 |
24,3 |
7353 |
9522 |
35,3 |
|
2007 г. |
32,6 |
1916 |
56,0 |
7875 |
10440 |
16,1 |
|
2008 г. |
19,7 |
2706 |
31,8 |
8112 |
9700 |
36,6 |
|
2009 г. |
27,3 |
3072 |
26,9 |
12715 |
9990 |
47,8 |
|
2010 г. |
25,8 |
3437 |
22,4 |
17146 |
21571 |
43,1 |
|
2011 г. |
23,1 |
4198 |
32,3 |
22248 |
27381 |
29,1 |
|
2012 г. |
31,7 |
4077 |
26,9 |
17553 |
23112 |
39,2 |
Парный коэффициент корреляции определяется по формуле:
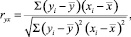 [1]
[1]
где yi, xi – значения соответственного результативного и факторного показателей в i-ый период времени; 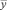 ,
,  – среднее арифметическое значение соответственно результативного и факторного показателей.
– среднее арифметическое значение соответственно результативного и факторного показателей.
Значение коэффициента парной корреляции лежит в интервале от –1 до + 1. Положительное значение коэффициента свидетельствует о прямой связи, отрицательное об обратной, т.е. когда с ростом фактора результат снижается. Чем ближе его значение к 1, тем теснее связь. Связь считается достаточно сильной, если значение коэффициента корреляции по абсолютной величине превышает 0,7, и слабой, если меньше 0,4; при равенстве его нулю связь полностью отсутствует. В модель включаются факторы, оказывающие сильное воздействие на результативный показатель. При этом нежелательно включать в корреляционно-регрессионную модель факторы, связь которых с результативным показателем носит функциональный характер. Не рекомендуется включать в модель те факторы, которые носят практически функциональный характер, т.е. коэффициент корреляции стремится к единице. Явление мультиколлинеарности в исходных данных считается установленным, если коэффициент парной корреляции между двумя переменными превышает 0,85 [1, 3]. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.
Расчет парных коэффициентов корреляции в работе осуществлен автоматизированным способом в среде MS Excel с помощью пакета Анализ данных и Опции Корреляция (табл. 2).
Как видно из данных табл. 2, зависимая переменная находится в слабой зависимости от некоторых выбранных факторов, а с некоторым факторами связь вообще отсутствует. При этом некоторые факторы сильно связаны между собой. Значения парных коэффициентов корреляции не превышают критические значения (0,85) для следующих пар факторов: первого и второго, первого и пятого, второго и третьего, второго и четвертого, второго и пятого, третьего и пятого, а также четвертого и пятого. Для остальных пар значение парного коэффициента корреляции выше 0,85. Это указывает на наличие явления мультиколлинеарности в исходных данных. Поэтому на основе этого из модели убирается третий фактор. Также необходимо удалить из модели второй фактор, так как значение парного коэффициента корреляции слишком малое – 0,03. Таким образом, в модель включаются не все факторы, а только первый, четвертый и пятый, которые переобозначаются соответственно в Х1–Х3.
Таблица 2
Матрица парных коэффициентов корреляции
|
Условное обозначение |
Y |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
|
Y |
1 |
|||||
|
Х1 |
–0,57 |
1 |
||||
|
Х2 |
0,03 |
–0,12 |
1 |
|||
|
Х3 |
–0,44 |
0,94 |
–0,15 |
1 |
||
|
Х4 |
–0,33 |
0,87 |
–0,12 |
0,96 |
1 |
|
|
Х5 |
–0,32 |
0,38 |
–0,79 |
0,27 |
0,11 |
1 |
В рамках второго и третьего этапов осуществляется проверка исходной информации на однородность, точность и подчинение закону нормального распределения. После этого моделируется вид связи между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение множественной регрессии. Выдвигается гипотеза, что между факторами и результативным показателем существует линейная связь, которая описывается уравнением множественной регрессии:
где А0 – свободный член уравнения при Х = 0;
Х1–Х3 – группа факторов, определяющих уровень изучаемого результативного показателя;
А1–А3 – коэффициенты регрессии при соответствующих факторных показателях, характеризующих уровень влияния факторов на результативный показатель в абсолютном выражении.
Для проверки исходной информации на однородность используются показатели: среднеквадратическое отклонение и коэффициент вариации.
Среднеквадратическое отклонение определяется по формуле:
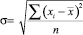 [3],
[3],
где xi – значение факторного показателя в i-м периоде;  – среднеарифметическое значение факторного показателя; n – количество наблюдений.
– среднеарифметическое значение факторного показателя; n – количество наблюдений.
Коэффициент вариации рассчитывается по следующей формуле:
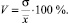
Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10 %, средней – если составляет 10–12 %, значительной, когда она больше 20 %, но не превышает 33 %. Если же вариация выше 33 %, то это говорит о неоднородности информации и необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки [3, 5].
Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.
Показатель асимметрии (А) и его ошибка (ma) рассчитываются по формулам:
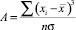 [1];
[1];
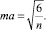
Показатель эксцесса (Е) и его ошибка (me) находятся по формулам:
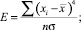
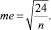
В симметричном распределении А = 0 отличие от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательное значение свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями.
В нормальном распределении показатель эксцесса Е = 0. Если Е больше нуля, то данные густо сгруппированы около средней, образуя островершинность. Если Е меньше нуля, то кривая распределения будет плосковершинной. Следует отметить, что если отношения А/ma и E/m меньше 3, то асимметрия и эксцесс не имеют существенного значения и исследуемая информация соответствует закону нормального распределения.
Аналогичным образом расчеты проводятся и для результативного показателя.
Проверка информации на однородность и соответствие закону нормального распределения осуществляется в среде MS Excel. Для этого используется пакет Анализ данных и опция Описательная статистика (табл. 3).
Таблица 3
Проверка исходной информации на однородность и соответствие закону нормального распределения
|
Наименование показателя |
Y |
X1 |
X2 |
X3 |
|
Среднее арифметическое значение |
29,23 |
2682,89 |
14493,67 |
34,54 |
|
Среднеквадратическое отклонение |
6,03 |
1073,22 |
7311,90 |
9,11 |
|
Коэффициент вариации |
20,6 |
40,0 |
50,4 |
26,4 |
|
Асимметрия |
0,11 |
0,28 |
1,02 |
–0,73 |
|
Ошибка асимметрии |
0,93 |
0,93 |
0,93 |
0,93 |
|
Отношение А/ma |
0,12 |
0,30 |
1,096 |
–0,78 |
|
Эксцесс |
–0,04 |
–1,68 |
–0,93 |
1,40 |
|
Ошибка эксцесса |
1,85 |
1,85 |
1,85 |
1,85 |
|
Отношение Е/mе |
0,022 |
0,908 |
0,503 |
0,757 |
Как видно из данных табл. 3 коэффициент вариации меньше 33 % только в результативном показателе и третьем факторе. По первому и второму факторам коэффициент вариации более 33 %, следовательно, вариации признаков не однородные. Отношения А/ma и Е/me для всех показателей по модулю меньше 3, поэтому асимметрия и эксцесс существенного значения не имеют. Таким образом, исходная информация является частично однородной, а следовательно, может использоваться в целях корреляционно-регрессионного анализа.
Параметры уравнения множественной регрессии определяются с помощью пакета Анализ данных и опции Регрессия. Согласно полученным результатам, уравнение множественной регрессии имеет вид:
Yxi = 37,4 – 0,0073Х1 + 0,0006Х2 + 0,055Х3.
Из данного уравнения видно, что между вторым, третьим факторами и результативным показателем существует прямая связь, а между первым фактором и результативным признаком – обратная связь. Действительно, с ростом цены реализации 1 ц мёда увеличивается прибыль, а следовательно, и растет рентабельность. Аналогично с ростом товарности, т.е. с увеличением продаж произведенного мёда растет и выручка, а соответственно, прибыль, а значит, и рентабельность [2, 4, 5].
В рамках четвертого и пятого этапов определяются основные показатели связи корреляционного анализа, а также производится статистическая их оценка и определяется возможность практического использования результатов корреляционно-регрессионного анализа. Проведем оценку модели на адекватность, т.е. осуществим проверку гипотез о предпосылках метода наименьших квадратов:
1. Гипотеза о близости к нулю математического ожидания остатков. Здесь используется критерий Стьюдента для остатков и проверяется нуль-гипотеза:
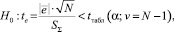
где SΣ – среднее квадратическое отклонение остатков – мера рассеяния остатков относительно своего среднего:
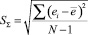 [3].
[3].
В нашем случае te = 0, так как е = 0 (табл. 4).
Табличное значение t-критерия Стьюдента при α = 0,05 и число степеней свободы = 9 – 1 = 8 составляет 2,306.
Таблица 4
Расчет средней величины остатков
|
t |
Y |
|
e |
|
1 |
39,7 |
34,4 |
5,3 |
|
2 |
33,7 |
33,9 |
–0,2 |
|
3 |
29,5 |
33,5 |
–4,0 |
|
4 |
32,6 |
31,4 |
1,2 |
|
5 |
19,7 |
26,0 |
–6,3 |
|
6 |
27,3 |
24,2 |
3,1 |
|
7 |
25,8 |
28,7 |
–2,9 |
|
8 |
23,1 |
26,2 |
–3,1 |
|
9 |
31,7 |
24,8 |
6,9 |
|
Итого |
263,1 |
263,1 |
0 |
Как видно, расчетное значение критерия меньше табличного. Это указывает на подтверждение нуль-гипотезы.
2. Гипотеза о статистической значимости коэффициента регрессии bi. Используя t-критерий Стьюдента, проверяем нуль-гипотезу:
Расчетное значение t-критерия Стьюдента составило 4,4 для А0; –1,54 для А1: 1,012 для А2; 0,208 для А3. Табличное значение t-критерия Стьюдента при α = 0,05 и число степеней свободы = 9 – 1 – 3 = 5 составляет 2,571. Сравнивая расчетные значения t-критерия Стьюдента (по абсолютной величине) с табличным значением, определяем значимость отдельных параметров регрессии. Как видно, вышеприведенное неравенство не выполняется для параметров А0. Это указывает на то, что только данный коэффициент является значимым.
3. Гипотеза о статистической значимости всего уравнения регрессии в целом. Используется критерий Фишера‒Снедекора F и проверяется нуль-гипотеза.
Расчетное значение F-критерия Фишера составило 1,659. Табличное значение выше указанного критерия при α = 0,05, К1 = m = 3, K2 = n – m = 9 – 3 = 6 составляет – 4,76 [1]. Как видно, расчетное значение F-критерия Фишера значительно ниже табличного. Это означает, что уравнение регрессии незначимо.
4. Оценка качества уравнения регрессии.
Для комплексной оценки качества уравнения регрессии используется коэффициент детерминации R2.
Коэффициент детерминации как мера качества уравнения модели характеризует долю вариации зависимой переменной, обусловленную регрессией (влиянием факторов) в общей вариацией результативной переменной Yi. Чем ближе коэффициент детерминации R2 к единице, тем лучше уравнение регрессии аппроксимирует экспериментальные данные, тем ближе эмпирические точки располагаются к линии регрессии, тем больше прогностическая сила модели.
Расчетное значение коэффициента детерминации составляет 0,4518, он показывает, что результативный признак всего на 45,18 % зависит от выбранных факторов, а на оставшиеся 54,82 % зависит от других факторов, не учтенных в модели. Так как коэффициент детерминации менее 0,9, это означает, что на основе данной модели невозможно получить достаточно точные значения результативного показателя.
Скорректированный коэффициент детерминации
В нашем случае скорректированный коэффициент детерминации составляет 0,123. Рассчитанное значение подтверждает предыдущий вывод о данной модели.
В комплексной оценке проделанной работы можно сказать, что полученная модель пригодна для прогнозировании на перспективу, что выбранные факторы оказывают влияние на результативный показатель, что связь между всеми выбранными факторами и результативным показателем, равная 0,67 – прямая и средняя.
Произведем прогноз результативного показателя на предстоящие два года. Для этого необходимо сначала спрогнозировать величину факторных показателей. Прогнозные значения факторных показателей Х1–Х3 в свою очередь определяются на основе построения их трендов, т.е. выявления тенденции изменения показателей во времени. Прогнозирование факторных показателей осуществляется в Excel с помощью Мастера диаграмм: опции Линия тренда. В данной опции, кроме линейной функции, предусмотрены возможности установления параметров логарифмической полиномиальной, степенной и экспоненциальной функций. Отбор тренда для каждого фактора осуществляется на основе критерия – коэффициента детерминации. При этом выбирается тренд с наибольшим значением R2 [2, 4].
Изменение всех факторных признаков во времени наиболее достоверно описывается трендами полиномиального вида:
Х1(t) = 18,158t2 – 199,85t + 1108,6,6;
Х2(t) = 414,88t2 – 1942,7t + 11069;
Х3(t) = –0,0648t2 + 1,8133t + 27,531.
Согласно значениям коэффициентов детерминации изменение показателей Х1–Х3 объясняется временным фактором соответственно на 95,84; 80,67 и 13,0 %.
Это свидетельствует о том, что все изменения факторов Х1, Х2, Х3 во времени точно описываются трендами полиномиального вида при приемлемом уровне.
Далее определяются прогнозные значения факторных показателей Х1–Х3 подставкой в соответствующие уравнения трендов по региону на 2013, 2014 гг.
На основе ранее определенных, прогнозных значений факторных показателей с помощью функции ТЕНДЕНЦИЯ осуществляется точечное прогнозирование результативного показателя Y по сельскохозяйственным организациям республики на 2013 и 2014 годы (табл. 5).
Таблица 5
Результаты точечного прогнозирования факторных показателей и результативного показателя
|
Год |
Период, t |
Х1 пр |
Х2 пр |
Х3 пр |
Y пр |
|
2013 г. |
10 |
3924,9 |
33130 |
39,2 |
32,5 |
|
2014 г. |
11 |
5504,1 |
39900 |
39,64 |
25,4 |
Как видно из данных табл. 5, ожидается, что затраты на одну пчелосемью в 2013 г. составят – 3924,9 руб., в 2014 г. – 5504,1 руб.; цена реализации 1 ц меда составит в 2013 г. – 33130 руб., в 2014 г. – 39900 руб.; уровень товарности соответственно 39,2 и 39,64 % от произведенного количества.
При указанных значениях факторных показателей и условии сохранения тенденции их изменения ожидаемое значение рентабельности в 2013 г. – 32,5 %, в 2014 г. – 25,4 %.
Обобщая вышесказанное, можно сделать вывод, что на основе полученной модели можно будет осуществлять прогнозирование рентабельности торговли медом на перспективу.
Рецензенты:
Хоружий Л.И., д.э.н., проректор по экономической работе и имущественному комплексу, профессор кафедры бухгалтерского учета (учетно-финансовый факультет), ФГБОУ ВПО «Российский государственный аграрный университет – МСХА имени К.А. Тимирязева», г. Москва;
Гайсин Р.С., д.э.н., профессор, заведующий кафедрой политической экономии, ФГБОУ ВПО «Российский государственный аграрный университет – МСХА имени К.А. Тимирязева», г. Москва.
Работа поступила в редакцию 11.04.2014.