Стратифицированные множества в том виде, в котором рассмотрим в данной работе их мы, имеют сравнительно короткую историю. Все полученные к данному моменту результаты можно разделить на две категории: результаты для одномерных стратифицированных множеств, именуемых геометрическими графами, и результаты для стратифицированных множеств более высоких размерностей. Результаты из первой категории уже образуют широкую теорию с большим количеством приложений, тогда как результаты, принадлежащие ко второй, начали появляться лишь менее 30 лет назад и пока что представлены не столь широко. В частности, к последним относится аналог неравенства Пуанкаре – Стеклова – Фридрихса:
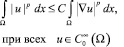
на стратифицированном множестве произвольной размерности. (Всюду далее мы будем называть его неравенство Пуанкаре (см. [7]), при том, что в таком виде данное неравенство было сформулировано Стекловым (см. [4]), а в литературе его нередко называют неравенством Фридрихса.) Доказан он был А.А. Гавриловым и О.М. Пенкиным при p = 2, см. [3, 6]. Однако, что касается случая с произвольным p ≥ 1, то до настоящего времени его доказательство никем сформулировано не было. Именно этот пробел и призвана устранить данная статья.
Чтобы получить достаточно полное представление о стратифицированных множествах и о текущем положении дел в данной области достаточно обратиться к книге [3], которая является главным и фактически единственным собранием результатов по этой теме.
Сразу стоит заметить, что схема доказательства для p = 2, приведенного в упомянутых работах, выглядит применимой и в общем случае. На первый взгляд, единственным фактическим отличием будет использование неравенства Гельдера вместо неравенства Коши – Буняковского – Шварца, которое, впрочем, является частным случаем первого. В то же время это доказательство представляется достаточно громоздким. Поэтому мы пойдем другим путем, используя простую идею, аналогичную одной из идей доказательства неравенства Соболева для произвольного p ≥ 1 на основании случая p = 1, например, см. [8, раздел 1.1.3].
Мы рассмотрим два типа неравенств Пуанкаре на стратифицированном множестве. Первый и основной – неравенство для случая жесткого лапласиана – будет нами рассмотрен относительно подробно. Второй – неравенство для случая мягкого лапласиана – мы лишь сформулируем. Для каждого из них неравенство будет иметь несколько разный вид и будет выполняться при различных условиях.
Далее мы приведем основные необходимые определения. Для справки см. [3, глава 9].
Основные определения
Пусть дано связное замкнутое множество Ω ⊂ Rn и пусть задан набор, который обозначим Σ, открытых подмногообразий σkj ⊂ Ω, называемых стратами, примыкающих друг к другу по типу клеточного комплекса. В обозначении σkj первый индекс означает размерность страта, а второй – его номер при автономной нумерации стратов данной размерности. Будем писать σkj < σli (или σli > σkj) и говорить, что σkj примыкает к σli, если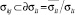 
. Страт σkj назовем свободным, если в Ω нет стратов, к которым бы он примыкал. Например, страты максимальной размерности всегда будут являться свободными.
Мы предполагаем выполненными следующие два условия для стратов из Σ:
1. Любые два страта не пересекаются, а их замыкания либо не пересекаются, либо пересечение их представимо в виде объединения стратов из Σ. Граница страта σkj является объединением стратов из Σ, размерность которых меньше k.
2. Для любого X ∈ σk–1,i «звезда»
допускает локальное (вблизи X) выпрямление, что означает существование такой окрестности V точки X в объемлющем пространстве Rn и такого диффеоморфизма Φ:V → W, что образ множества V Ç S представляет собой объединение (k – 1)-мерного шара (образа части σk–1,i, попавшей в V) и примыкающих к нему полушарий (аналогичных образов частей σkj).
Для иллюстрации второго условия приведем следующий рис. 1.
По нашему определению, стратифицированное множество – это тройка (Ω, Φ, φ), где φ – отображение, описывающее «склейку» Ω из стратов семейства Σ), но для простоты будем называть стратифицированным множеством само Ω.
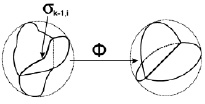
Рис. 1
Топология на Ω индуцируется стандартной топологией пространства n, т.е. подмножество Ω0 стратифицированного множества Ω называется открытым, если существует открытое подмножество n, пересечение которого с Ω совпадает с Ω0. Пусть Ω0 – связное и открытое подмножество Ω, составленное из стратов семейства Σ и такое, что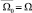 
.
Тогда разность Ω\Ω0, очевидно, является границей множества Ω0 и будет тоже состоять из стратов, а потому будет обозначаться через ∂Ω0). Под обозначением Ω = (Ω0, ∂Ω0) мы будем понимать, что данное стратифицированное множество Ω разбито на Ω0 и ∂Ω0 указанным способом.
Далее, введем на стратифицированном множестве меру. Подмножество ω Ì Ω назовем измеримым, если измеримы по Лебегу пересечения ω Ç σkj при всех значениях индексов k и j, а его меру определим, как
,
где μk есть – мерная мера Лебега на σkj. Нетрудно заметить, что так определенные измеримые множества образуют σ-алгебру, а функция μ является мерой. Измеримость функции по мере μ определяется точно так же, как и в классическом случае. Меру μ назовем стратифицированной мерой.
Интеграл Лебега суммируемой функции f на Ω оказывается равным сумме интегралов Лебега сужений этой функции на отдельные страты, т.е.
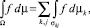
где суммирование проводится по всем стратам.
Пусть Ω = (Ω0, ∂Ω0), обозначим через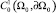 
множество непрерывных на Ω функций, которые обращаются в нуль на ∂Ω0, и сужения которых на замыкание любого страта из Ω0 являются непрерывно дифференцируемыми функциями. Теперь мы можем определить стратифицированный аналог пространства 
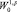как пополнение пространства 
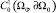по норме
где ∇f на каждом k-мерном страте есть классический k-мерный градиент сужения функции f на данный страт. Обозначать полученное пространство будем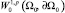 
.
Неравенство Пуанкаре на стратифицированном множестве для жесткого лапласиана
Как уже было сказано, мы будем опираться на случай p = 2, для выполнения которого требуется соблюдение условия «прочности» рассматриваемого стратифицированного множества. Поэтому будет естественным взять то же самое требование за основу и в общем случае. При этом, как покажет доказательство, никаких изменений в связи с переходом к произвольному р данное условие не потребует.
Определение 1. Стратифицированное множество Ω = (Ω0, ∂Ω0) назовем прочным, если для любого страта σki ∈ Ω0 найдется цепочка (упорядоченный набор) стратов 
такая, что:
1) любые два соседних страта из цепочки примыкают один к другому, а их размерности отличаются друг от друга ровно на единицу;
2) последний страт цепочки входит в ∂Ω0.
Такую цепочку будем называть прочной цепочкой, построенной для страта σki.
В качестве примера рассмотрим рис. 2.
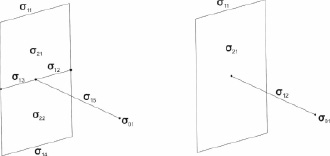
Рис. 2
Здесь жирными точками обозначены нульмерные страты. Если граница обоих изображенных на рисунке стратифицированных множеств будет выбрана состоящей лишь из одного страта – σ01, то в этом случае множество, изображенное слева, удовлетворяет условию прочности, а множество справа – нет. Если же к границе множества справа добавить еще и страт σ11 (вместе с его граничными стратами), то оно также станет прочным.
Теорема 1
Пусть дано прочное стратифицированное множество Ω = (Ω0, ∂Ω0) и p ≥ 2. Тогда найдется константа C > 0, зависящая только от Ω и p, такая, что для любой функции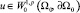 
выполнено неравенство
(1)
Доказательство: Возьмем произвольную функцию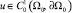 
и положим 
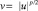. Легко видеть, что 
. В самом деле, v дифференцируема почти всюду (относительно стратифицированной меры) и в точках дифференцируемости мы имеем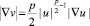 
, а тогда
Далее применим к центральной части неравенство Гельдера с показателями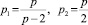 
. В результате получим
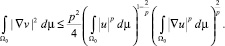(2)
С другой стороны, так как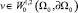 
, то в силу неравенства Пуанкаре на стратифицированном множестве для p = 2 будем иметь
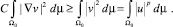(3)
Собрав вместе неравенства (2) и (3), мы получим требуемое неравенство (1) для функций из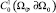 
.
Что касается произвольной функции w из 
, то здесь достаточно заметить, что, по определению, найдется последовательность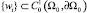 
, что
■
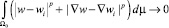Вернемся к множеству, изображенному на рис. 1 справа. Для него, как нетрудно убедиться, теорема 1 выполняться не будет. Действительно, рассмотрим функции из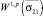 
(классическое пространство), которые обращаются в нуль только в одной точке (в качестве таковой выберем точку, составляющую страт σ02). Известно, что для такого класса функций классическое неравенство Пуанкаре
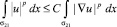
выполняться не будет. Продолжив каждую из них нулем на страты σ12 и σ01, мы получим подмножество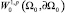 
, для которого утверждение теоремы 1 неверно. В общем случае, в работе [2] приводится доказательство необходимости условия прочности в неравенстве Пуанкаре на стратифицированном множестве для жесткого лапласиана. И хотя там оно сформулировано для случая p = 2, убедиться в его справедливости при произвольном p не представляет из себя никакой сложности. Таким образом, условие прочности является необходимым и достаточным для выполнения неравенства (1).
Неравенство Пуанкаре на стратифицированном множестве для мягкого лапласиана
Неравенство Пуанкаре для мягкого лапласиана существенным образом отличается от рассмотренного выше случая. В нем не учитываются значения функции на стратах, не являющихся свободными, т.е. на тех, которые содержатся в границе какого-либо иного страта из Ω. Другими словами, неравенство Пуанкаре на стратифицированном множестве для случая мягкого лапласиана имеет вид:
(4)
где q ≡ 1 на свободных стратах и равно нулю на остальных. В результате это приводит к некоторому изменению требований, предъявляемых к стратифицированному множеству, в сравнении со случаем жесткого лапласиана. Во-первых, к стратам, не являющимся свободными, более не предъявляются никакие требования. Это выглядит естественным, если учесть, что они никак не влияют на неравенство (4). В то же время к свободным стратам, наоборот, предъявляются существенно более жесткие условия. А именно: для каждого из них должна существовать прочная цепочка, причем такая, что размерности стратов в ней должны чередоваться, а все страты той же размерности, что и исходный, должны быть свободными. То есть, прочная цепочка, построенная для свободного страта размерности k, должна содержать только страты размерностей k и k – 1, причем страты размерности k должны быть также свободными. Так, например, множество, изображенное на рис. 1 слева, не удовлетворяет описанным требованиям, если его граница состоит только из σ01, но будет удовлетворять, если граница будет состоять из объединения страта σ01 и замыкания σ11.
Необходимость и достаточность приведенных условий практически очевидны. Для иллюстрации необходимости подойдет пример, аналогичный тому, который приведен в конце предыдущего пункта и показывает необходимость условий теоремы 1. А по поводу достаточности мы лишь отметим, что в этом случае ситуация ничем не отличается от классической.
В заключение стоит сказать об аналоге неравенства Соболева на стратифицированном множестве, который, несомненно, представляет большой интерес и который включает в себя приведенные в данной работе результаты. К данному моменту этот вопрос полностью не решен. Частичный результат можно найти в [1], где приведены чрезмерно грубые требования к рассматриваемому стратифицированному множеству, а само доказательство громоздко и достаточно примитивно. В общем случае требования к множеству, по-видимому, будут очень близки к тем, что мы имеем здесь, но само доказательство должно отличаться куда большей тонкостью, нежели доказательство неравенства Пуанкаре.
Рецензенты:
Каменский М.И., д.ф.-м.н., профессор, заведующий кафедрой функционального анализа и операторных уравнений, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж;
Новиков И.Я., д.ф.-м.н., профессор кафедры функционального анализа и операторных уравнений, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж;
Кульбачинский В.А., д.ф.-м.н., профессор кафедры физики низких температур и сверхпроводимости, физический факультет, Московский государственный университет им. М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 05.02.