В настоящее время создана математическая теория, разработаны и внедрены в промышленность одноствольные строительные артиллерийские орудия [5]. Применение на практике строительных пушек показало их большую эффективность в нефтегазовом и промышленном строительстве.
Однако основным недостатком созданных орудий является невозможность их использования для застреливания свай на большие глубины при помощи одного выстрела. Так, например, максимальная величина проникания свай в глинистый грунт с консистенцией 0,5 при использовании установки УЗАС-2, созданной на базе модернизированного крупнокалиберного артиллерийского орудия М-47 [4], составляет 3,8 м [2]. Поэтому перед разработчиками строительных пушек встала задача создания артсистемы, способной застреливать сваи на глубину до 8 м. В работе [1] была предложена принципиальная схема многоствольных откатных пушек. На рисунке приведена эта принципиальная схема.
Работает установка следующим образом. В стволы 1 вставляется фигурный поршень 3 с платформой 2, которая опирается на строительный элемент 4, упирающийся на поверхность грунта 5. Во время выстрела платформа 2 давит на сваю 4, в результате чего свая 4 проникает в грунт 5.
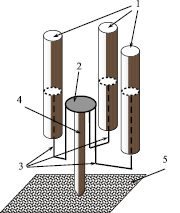
Принципиальная схема многоствольной строительной артиллерийской системы
При работе многоствольных строительных артсистем возникает задача выбора условий заряжания таким образом, чтобы предварительный период выстрела завершался одновременно в каждом орудии, входящем в многоствольную конструкцию, поэтому аткуальной является задача математического моделирования предварительных периодов выстрела для каждого из стволов.
Описание численно-аналитического способа
Пусть n – количество стволов, входящих в многоствольную артиллерийскую систему.
Введем следующие допущения:
1. Состав продуктов горения во время выстрела не меняется, величина силы пороха f и коволюма пороховых газов α постоянны.
2. Показатель адиабаты (θ + 1) пороховых газов принимается постоянным, равным некоторому среднему значению.
3. Предполагается, что строительный элемент стоит на месте, пока давление газов не достигает величины давления форсирования p0,i, где i – номер ствола в многоствольной строительной артиллерийской системе, 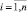 .
.
4. Растяжением стенок ствола при выстреле и прорывом газов через зазоры между строительным элементом и каналом ствола пренебрегается.
5. Орудия, входящие в многоствольную строительную артиллерийскую систему, имеют разные технические характеристики и условия заряжания.
6. При выстреле используется трубчатый зерненый порох.
Пусть известны значения давлений форсирования p0,i, 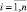 в каждом из стволов.
в каждом из стволов.
Согласно работе [3] относительную часть сгоревшего пороха в предварительном периоде выстрела можно рассчитать по формуле
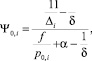
где i – номер ствола; Ψ0,i – относительная часть сгоревшего пороха в конце предварительного периода выстрела в стволе i; 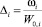 – плотность заряжания; ωi – масса заряда в стволе i, W0,i – объем каморы в стволе i, δ – плотность пороха; f – сила пороха; p0,i – давление форсирования в стволе i, здесь
– плотность заряжания; ωi – масса заряда в стволе i, W0,i – объем каморы в стволе i, δ – плотность пороха; f – сила пороха; p0,i – давление форсирования в стволе i, здесь 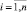 .
.
На основе работы [2] легко показать, что энергия Ei, выделяемая при горении пороховых газов в предварительном периоде выстрела в стволе i, описывается соотношением
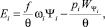
где 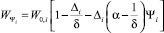 – свободный объем каморы i-го ствола к моменту сгорания в ней части заряда Ψi.
– свободный объем каморы i-го ствола к моменту сгорания в ней части заряда Ψi.
Так как в предварительном периоде выстрела пороховые газы не совершают внешних работ, то справедливо равенство
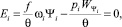
которое влечет соотношение
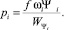 (1)
(1)
Согласно геометрическому закону горения трубчатого зерненого пороха справедливо равенство [3]
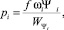 (2)
(2)
где t – время; Ipi – импульс пороха в стволе i.
Подставляя соотношение (1) в выражение (2), получим равенство
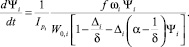 (3)
(3)
Легко видеть, что соотношение (3) является обыкновенным дифференциальным уравнением в разделяющихся переменных, решение которого определяется формулой
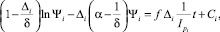 (4)
(4)
где Ci – произвольная постоянная.
Так как первоначальное давление в каморах равно атмосферному pa, то будем считать, что справедливы соотношения
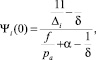
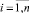 (5)
(5)
Учитывая равенства (5), можно вычислить значения Ci по формулам
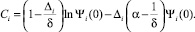
Зная величины Ci, можно из соотношения (4) определить продолжительность ti предварительного периода в каждом из стволов:
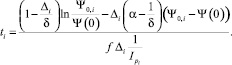
Пусть минимальное время горения заряда (ствол k) в предварительном периоде выстрела до достижения давления форсирования p0,k. Тогда очевидно, что воспламенять заряды в стволах многоствольной артиллерийской системы нужно раньше, чем в стволе k на время λi, удовлетворяющее соотношению λi = ti – tk, 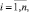 t ≠ k.
t ≠ k.
Пример реализации способа
Рассмотрим использование предложенного способа расчета предварительных периодов выстрела для двуствольной строительной артиллерийской системы, условия заряжания которой приведены в табл. 1.
Таблица 1
Условия заряжания
|
Условие заряжания |
Значение параметра |
|
W0,1, м3 |
0,001026 |
|
W0,2, м3 |
0,00063 |
|
Ip1, Па с |
230000 |
|
Ip2, Па с |
37650 |
|
p0,1, МПа |
30 |
|
p0,2, МПа |
30 |
|
ω1, кг |
0,154 |
|
ω2, кг |
0,154 |
Таблица 2
Результаты расчетов
|
Расчетное время горения пороха в каморе |
|
|
первого ствола, с |
второго ствола, с |
|
0,00802 |
0,00754 |
Расчетное время опережения порохового заряда в каморе первого ствола относительно воспламенения пороха в каморе второго ствола (табл. 2) составило 0,00048 с.
Заключение
Таким образом, предложенный в статье аналитический способ оценки времени воспламенения пороховых зарядов в камерах многоствольных строительных артиллерийских орудий позволяет без применения приемов программирования получить необходимые характеристики предварительных периодов выстрела, что облегчает проектирование и расчет строительных артсистем.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (базовая часть государственного задания на проведение научно-исследовательских работ).
Рецензенты:
Пенский О.Г., д.т.н., доцент, профессор кафедры фундаментальной математики, Пермский государственный национальный исследовательский университет, г. Пермь;
Ясницкий Л.Н., д.т.н., профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.
Работа поступила в редакцию 04.04.2014.



