Комбинированные системы управления широко используются при управлении технологическими процессами [1]. Реализация принципов управления по отклонению и по возмущению в одной системе позволяет значительно улучшить качество переходного процесса в системе управления. Эффективность этих систем обусловлена возможной компенсацией основных контролируемых возмущающих воздействий.
Отсутствие возможности полной компенсации в связи со сложностью реализации идеального компенсатора и наличия неконтролируемых возмущений накладывает на управляющее устройство в обратной связи задачу стабилизации регулируемой переменной. За счет частичной компенсации основных возмущающих воздействий контур обратной связи значительно улучшает качество переходного процесса по величине перерегулирования и по времени регулирования по сравнению с одноконтурной системой без компенсаторов возмущений.
Для аналоговых систем вопрос выбора реальных компенсаторов освещен достаточно широко. В работе [2] предложен графоаналитический метод расчета настроечных параметров реальных дифференцирующих и интегро-дифференцирующих звеньев. В работах [3, 4] предложен аналитический метод расчета настроечных параметров указанных звеньев, а также дополнительно введено в рассмотрение в качестве реального компенсатора неминимальнофазовое инерционное звено [5].
Обзор публикаций в области синтеза цифровых комбинированных систем управления [6–7] показал, что при параметрическом синтезе этих систем ограничиваются определением передаточных функций идеальных компенсаторов.
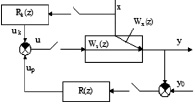
В данной работе ставится задача параметрического синтеза компенсирующих устройств в цифровых комбинированных системах управления. На рис. 1 показаны возможные варианты включения компенсаторов в цифровых системах управления.
 а
а 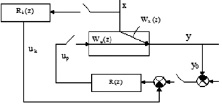 б
б
Рис. 1. Структурные схемы цифровых комбинированных систем управления при подаче компенсирующего сигнала: а – на вход объекта; б – на вход стабилизирующего регулятора
Нами предложен частотный метод параметрического синтеза цифровых одноконтурных систем управления с пропорционально-интегральными (ПИ) и пропорционально-дифференциальными (ПД) – законами регулирования, реализованными в дискретной форме [8]. В работе [9] предложен частотный метод параметрического синтеза цифровых одноконтурных систем управления с пропорционально-интегрально-дифференциальным (ПИД) законом управления, реализованным в дискретной форме.
Работы [8, 9] дают возможность определять рабочую частоту цифровой одноконтурной системы, которая используется при синтезе компенсаторов.
При выборе реального компенсатора в аналоговых системах используется следующий алгоритм:
1. Рассчитывают оптимальные настроечные параметры выбранного типа регулятора и соответствующую им рабочую частоту.
2. Рассчитывают амплитудно-фазовые характеристики (АФХ) объекта управления каналам управления Wоу(jω) и возмущения Wов(jω).
3. Рассчитывают АФХ идеального компенсатора как 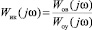 в случае подачи компенсирующего сигнала на вход объекта управления или как
в случае подачи компенсирующего сигнала на вход объекта управления или как 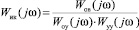 в случае подачи компенсирующего сигнала на вход стабилизирующего регулятора Wуу(jω).
в случае подачи компенсирующего сигнала на вход стабилизирующего регулятора Wуу(jω).
4. Выбирают тип реального компенсатора для удовлетворения следующих условий:
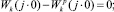 (1)
(1)
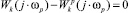 (2)
(2)
или
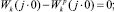 (3)
(3)
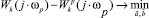 (4)
(4)
или
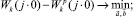 (5)
(5)
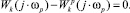 (6)
(6)
5. Вычисляют настройки выбранного типа компенсатора.
Руководствуясь этой методикой, выполнены все этапы параметрического синтеза цифровой комбинированной системы с дискретной реализацией ПИ – закона управления управляющего устройства. На каждом этапе проводилось сравнение результатов, полученных для аналогового и цифрового вариантов.
Для сравнения взяты результаты параметрического синтеза аналоговых комбинированных систем управления из [4].
Передаточные функции объекта управления:
а) для аналогового варианта
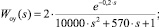
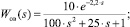
б) для цифрового варианта (переход выполнялся по Тастину [8])
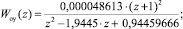
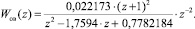
Амплитудно-фазовые характеристики
а) для аналогового варианта выполнялась замена
s = jω;
б) для цифрового варианта выполняется билинейное преобразование [6]
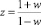
с последующим переходом на круговую частоту по выражению
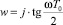 для
для 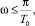
где ω – круговая частота; T0 – шаг квантования (дискретизации). При выборе шага квантования использованы рекомендации [6].
Графики АФХ объекта управления для аналогового и дискретного вариантов приведены на рис. 2 и 3.
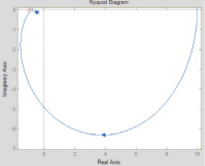 а
а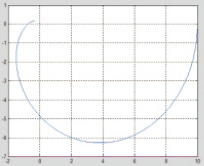 б
б
Рис. 2. Амплитудно-фазовые характеристики объекта по каналу возмущения: а – для аналогового варианта; б – для дискретного варианта
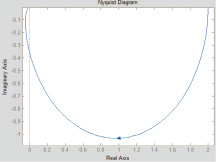 а
а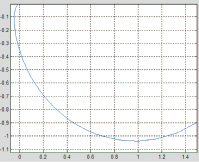 б
б
Рис. 3. Амплитудно-фазовые характеристики объекта по каналу управления: а – для аналогового варианта; б – для дискретного варианта
На рис. 4 приведены АФХ идеальных компенсаторов для аналогового и дискретного вариантов.
Для аналогового варианта выбран реальный компенсатор в виде интегро-дифференцирующего звена с передаточной функцией 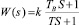 . По Тастину [6] дискретная передаточная функция реального компенсатора имеет вид
. По Тастину [6] дискретная передаточная функция реального компенсатора имеет вид
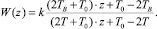
Расчет параметров k, TВ и T реального компенсатора в цифровой системе управления осуществлялся при соблюдении условий (1) и (2) по алгоритму, приведенному в [4].
 а
а 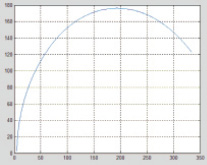 б
б
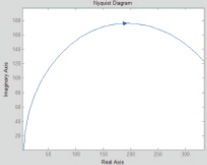
Рис. 4. АФХ идеального компенсатора: а – для аналогового варианта; б – для цифрового варианта
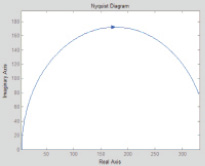
На рис. 5 показаны АФХ реальных компенсаторов для аналогового и дискретного вариантов.
Сравнение АФХ объекта управления, сравнение АФХ идеальных и реальных компенсаторов и сравнение переходных процессов в аналоговых и цифровых системах управления свидетельствует об их идентичности. Аналогичное сравнение было выполнено для всех рассмотренных случаев в работах [3–5]. Установлена также полная идентичность для аналогового и дискретного вариантов. Следовательно, аналитический метод расчета компенсирующих устройств, предложенный в работах [3–5], может быть применен при параметрическом синтезе цифровых комбинированных систем управления.
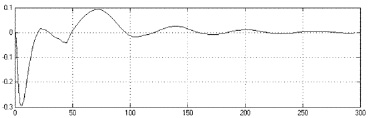
На рис. 6 показаны переходные процессы комбинированных систем управления для аналогового и дискретного вариантов.
Заключение
При параметрическом синтезе цифровых комбинированных систем управления для вычисления настроек реальных компенсаторов справедливы математические выражения, полученные для расчета аналоговых реальных компенсаторов.
 а
а 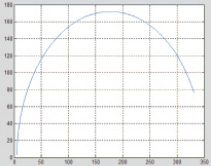 б
б
Рис. 5. Амплитудно-фазовые характеристики реального компенсатора для аналогового (а) и дискретного (б) вариантов
 а
а
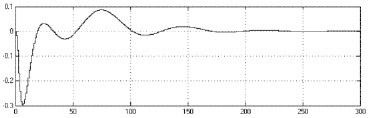 б
б
Рис. 6. Переходные процессы комбинированных систем для (а) аналогового и (б) дискретного вариантов
Рецензенты:
Игнатюк В.А., д.ф.-м.н., профессор кафедры электроники, Владивостокский государственный университет экономики и сервиса, г. Владивосток;
Шахгельдян К.И., д.т.н., начальник управления научно-технического обеспечения, Владивостокский государственный университет экономики и сервиса, г. Владивосток.
Работа поступила в редакцию 01.04.2014.



