В [7, 9] был предложен аналитический метод расчёта потоковой индуктивности токового кольца с конечной радиальной шириной, который основывался на законе Био ‒ Савара ‒ Лапласа для геометрического проводника [4]. Этот же метод был применён для расчёта коэффициента увеличения индуктивности спирального типа [5]. Учёт конечности поперечного сечения проводника при нахождении распределения магнитных полей требует применения фундаментальных законов магнитостатики. Таким методом была рассчитана погонная индуктивность цилиндрических проводников с аксиальной плотностью тока [8].
Сохраняя идеологию методики расчёта, предложенной в [1–3, 5–9], рассчитаем погонную индуктивность цилиндрического коаксиального кабеля, в котором векторы плотности тока центральной жилы и оплётки имеют аксиальные направления.
Физико-математическая модель расчёта
Расчёт будем проводить исходя из фундаментального уравнения магнитостатики, записанного для векторного потенциала
(1)
с калибровкой
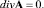(2)
Связь индукции магнитного поля с векторным потенциалом находится из соотношения
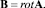(3)
Запишем (1) в цилиндрических координатах. Учтем, что плотности тока в коаксиальном кабеле имеют только одну аксиальную компоненту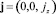 
, направленную по оси z, а сама плотность тока складывается из двух составляющих: плотности тока, текущего в центральной жиле j0, и тока, текущего по оплётке j1. Они порождают поле векторного потенциала, имеющего также только одну компоненту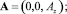 
(4)
Оператор Лапласа в уравнении (1) для декартовой компоненты векторного потенциала, зависящей от радиуса, имеет вид
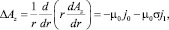(5)
где σ – знаковый множитель. Для сонаправленных токов он принимает значение +1, а для токов противоположного направления – 1.
Предположим, что в (5) обе плотности токов однородны по поперечному сечению, коаксиальный кабель имеет внешний радиус R, а геометрия его поперечного сечения представлена на рис. 1.
На рис. 1 введены обозначения: r1 – внешний радиус первой области (радиус проводника центральной жилы); r2 – внешний радиус второй немагнитной области; R – внешний радиус оплётки коаксиального кабеля; r – текущий радиус цилиндра. Всегда выполняется условие r1 < r2 < R.
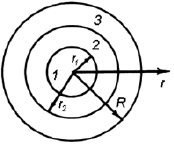
Рис. 1. Поперечное сечение коаксиального кабеля
Из (3) следует, что такое поле векторного потенциала в каждой области коаксиального кабеля порождает индукцию магнитного поля с одной компонентой
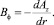(6)
Распределение векторного потенциала внутри коаксиального кабеля
Цилиндрическая поверхность коаксиального кабеля, имеющего внешний радиус R, содержит внутри себя области, в которых возбуждено статическое магнитное поле (рис. 1). Их три: область 1 (0 ≤ r ≤ r1), в которой есть ток j0; внутренняя область 2, в которой r1 ≤ r ≤ r2 и токов нет; и внешняя область 3 (r2 < r < R), где есть ток j1. Поставленная задача очень похожа на задачу электростатики для уравнения Пуассона (внутренняя краевая задача с тремя границами).
Тогда для области 1 (потенциал и индукция далее отмечены индексом «1») уравнение (5) имеет вид
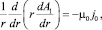(7)
а во второй области на рис. 1 (потенциал отмечен индексом «2») –
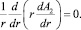(8)
В уравнении (5) перейдём к новой функции
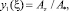
где ξ = r/R, в области 0 ≤ ξ ≤ ξ1, а
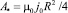(9)
– масштаб векторного потенциала, одинаковый во всех областях.
Решение (7) для области 1 имеет вид
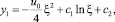(10)
где
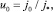(11)
а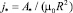 
– масштаб плотности тока. Калибруя векторный потенциал по условию y1(0) = 0 (тогда c1 = c2 = 0), приходим к решению в области 1, имеющему вид
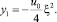(12)
Решение уравнения (8) для области 2 (ξ1 ≤ ξ ≤ ξ2) имеет вид
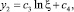(13)
где с3, с4 – произвольные постоянные
Распределение векторного потенциала в области 3 (ξ2 ≤ ξ ≤ 1) получается из решения уравнения
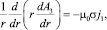
которое в безразмерных переменных имеет вид
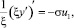(14)
где u1 связано с масштабом плотности тока соотношением
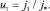(15)
Решение (14) в области 3 (ξ2 ≤ ξ ≤ 1) имеет вид
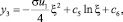(16)
где с5, с6 – произвольные постоянные. Все произвольные постоянные должны быть определены в процессе решения граничной задачи.
Распределение индукции магнитного поля внутри коаксиального кабеля
Радиальное распределение индукции в трёх областях находим из (6)
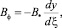(17)
где
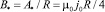(18)
– масштаб индукции магнитного поля.
В первой области 0 ≤ ξ ≤ ξ1 получим
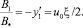(19)
Из (19) следует, что вектор индукции магнитного поля в области 0 ≤ ξ ≤ ξ1 сонаправлен с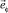 
(единичный азимутальный вектор) и линейно нарастает с радиусом r системы.
Во второй области ξ1 ≤ ξ ≤ ξ2 получим
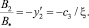(20)
Из (20) следует, что вектор индукции магнитного поля в области ξ1 ≤ ξ ≤ ξ2 при c3 < 0 также сонаправлен с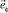 
и убывает с ростом радиуса r системы.
В области 3 ξ2 ≤ ξ ≤ 1 получим
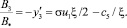(21)
Из (21) следует, что вектор индукции магнитного поля в области ξ2 ≤ ξ ≤ 1 при с5 < 0 может быть сонаправлен с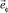 
при σ = +1, а может быть противоположного направления с 
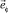при σ = –1. Уточнение распределения индукции и векторного потенциала магнитного поля коаксиального кабеля может быть проведено после определения произвольных постоянных на трёх границах системы.
Постоянные с3 и с4 определяем из условия непрерывности функции потенциала и её производной на границе областей ξ = ξ1
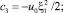(22)
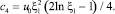(23)
Постоянную c5 определяем из требования равенства нулю индукции магнитного поля на внешнем радиусе R
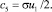(24)
Постоянную c6 определяем из равенства потенциалов на границе ξ2
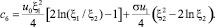(25)
Как видно из значений найденных произвольных постоянных, индукция магнитного поля в первой области положительная и линейно нарастающая. Во второй области она положительна, но всегда убывающая. Затем при переходе через границу раздела ξ2 индукция испытывает скачок. Во время скачка знак индукции может либо измениться, либо нет. При значении знаковой функции σ = +1 (оба тока в кабеле одинакового направления) индукция становится отрицательной и при ξ = 1 она равна нулю. При значении знаковой функции σ = –1 (токи кабеля имеют противоположные направления) она остаётся положительной, испытывает либо положительный, либо отрицательный скачок и при ξ = 1 обращается в нуль.
Индуктивности коаксиального кабеля
Полная индуктивность L коаксиального кабеля складывается из трёх индуктивностей:
1) токовой L1, которая возникает в области 1;
2) потоковой L2, которая характеризует область 2;
3) токовой L3, которая возникает в области 3. А именно:
L = L1 + L2 + L3. (26)
Поясним, что мы под этим понимаем. Наличие трёх областей, в которых магнитное поле распределено по разным законам, указывает на то, что индуктивность прямолинейного круглого тока складывается из трёх частей. Первая часть соответствует индуктивности, которая связана с потоком магнитного поля в области 1. В ней силовые линии магнитного поля поперечны линиям плотности тока. В связи с этим её удобно назвать первой токовой частью коаксиальной индуктивности.
Вторая часть соответствует индуктивности, которая связана с магнитным потоком, находящимся в области 2. В этой области нет тока, поэтому её удобно назвать потоковой частью коаксиальной индуктивности. Третья часть соответствует индуктивности, которая связана с потоком магнитного поля в области 3. В ней силовые линии магнитного поля снова поперечны линиям плотности тока. В связи с этим её удобно назвать второй токовой частью коаксиальной индуктивности.
Если цилиндрический коаксиальный кабель разрезать по оси (рис. 2), то видна область, по которой следует интегрировать при вычислении потока в области 1. Ось проводника обозначена ОО’, а элементарная площадка интегрирования dS – заштрихована. Для областей 2 и 3 площадка dS перемещается в соответствующую область.
Вычисляя магнитный поток в области 1, получим
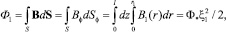(27)
где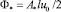 
– масштаб потока. Между током в области 1 и потоком существует базовая связь
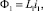(28)
где L1 – первая токовая коаксиальная индуктивность. Подставляя в (28) ток, выраженный через плотность тока и площадь области 1, получим погонную индуктивность в виде
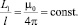(29)
Как видно из (29), она с точностью до постоянной величины совпадает с магнитной постоянной.
Рассуждая аналогично для области 2, получим
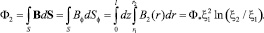(30)
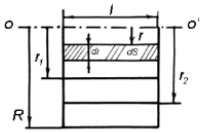
Рис. 2. Площадка интегрирования при вычислении потока в области 1
Применяя (28) для тока i1 и потока Ф2, получим для второй коаксиальной потоковой погонной индуктивности величину, зависящую от отношения приведённых радиусов границ системы
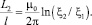(31)
Вычисление третьей токовой погонной индуктивности сводится к вычислению потока, в котором индукция, а стало быть, и поток в области интегрирования может быть отрицательной (зависит от знака σ):
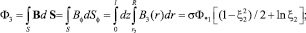(32)
где масштаб потока
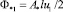. (33)
Значение магнитного потока будет положительно (токи текут в противоположные стороны) при σ = –1, и отрицательно, если токи в коаксиальном кабеле текут сонаправленно.
Ток, создающий поток Ф3, складывается из всех токов, протекающих в системе
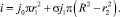(34)
Учитывая связь (28) между Ф3 и (34), получим для второй токовой погонной индуктивности кабеля соотношение
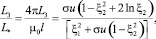(35)
где
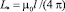(36)
– масштаб индуктивности,
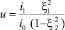(37)
– параметр, связанный с отношением токов, протекающих в коаксиальном кабеле.
В табл. 1 приведены значения второй токовой индуктивности в зависимости от отношения токов u. Её значения вычислены при следующих предположениях: ξ1 = 0,25; ξ2 = 0,75; токи сонаправленны (σ = +1).
Таблица 1
Приведённые значения второй токовой индуктивности при токах одного направления (σ = +1)
|
i1/i0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
|
–L3/L* |
0,53 |
0,90 |
0,12 |
0,14 |
0,16 |
0,17 |
0,18 |
0,19 |
0,20 |
0,21 |
Как видно из табл. 1, вторая токовая индуктивность всегда отрицательная. Физические причины этого становятся понятными. Индуктивность с ростом отношения токов сначала увеличивается почти в два раза, затем начинает падать, а потом снова медленно увеличиваться. Индуктивность может изменяться в четыре раза при изменении отношения токов в десять раз.
Полная индуктивность кабеля для выбранных расчётных значений оказывается всегда положительной величиной.
В табл. 2 приведены значения второй токовой индуктивности в зависимости от отношения токов. Значения вычислены при следующих предположениях: ξ1 = 0,25; ξ2 = 0,75; токи имеют противоположное направление (σ = –1).
Таблица 2
Приведённые значения второй токовой индуктивности при токах противоположного направления (σ = –1)
|
i1/i0 |
0,85 |
0,90 |
0,95 |
1,05 |
1,1 |
1,15 |
1,20 |
|
L3/L* |
1,79 |
2,84 |
5,99 |
–6,62 |
–3,47 |
–2,42 |
–1,89 |
Как видно из табл. 2, в этом случае вторая токовая индуктивность может быть как положительной, так и отрицательной. Она может принимать большие значения в области, где токи становятся близки друг другу по величине. В этом случае знаменатель выражения (35) обращается в нуль при выполнении условия
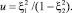(38)
Тогда возможен случай, когда величина L3/L* = –6,62 при значении отношения токов 1,05 (табл. 2). При таких больших значениях второй токовой индуктивности полная индуктивность коаксиального кабеля будет отрицательной
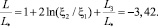
Полученные значения индуктивности следует считать идеализированными, поскольку вычисления проводились на постоянном токе. Эти же значения могут реализоваться на переменном токе на частотах, при которых фазовый сдвиг между током и потоком будет близок к нулю.
Выводы
- Предложен аналитический метод расчёта радиального распределения векторного потенциала и индукции магнитного поля в бесконечно длинном коаксиальном кабеле.
- Уравнение магнитостатики, записанное для векторного потенциала, решается для трёх областей коаксиального кабеля, на которых сформулированы граничные условия.
- Радиальное распределение магнитной индукции таково, что в первой области она положительна и линейно нарастает с увеличением радиуса.
- Во второй области магнитная индукция убывает с ростом радиуса, оставаясь положительной.
- При переходе через границу раздела между второй и третьей областями индукция магнитного поля испытывает скачок. Скачок может быть как со сменой знака, так и без нее.
- Когда оба тока в кабеле имеют одинаковые направления, то индукция в третьей области становится отрицательной, а при ξ = 1 она равна нулю.
- Когда оба тока в кабеле имеют противоположные направления, индукция магнитного поля в этой области остаётся положительной, но испытывает либо положительный, либо отрицательный скачок и при ξ = 1 обращается в нуль.
- Полная индуктивность коаксиального кабеля складывается из трёх погонных индуктивностей: двух токовых, которые возникают в областях 1 и 3, и одной потоковой, которая формируется в области 2.
- Вычисление первой токовой индуктивности показывает, что её значение пропорционально магнитной постоянной.
- Вычисление потоковой индуктивности указывает на то, что её значение оказывается пропорциональным логарифму отношения радиусов второй и первой областей.
- Вычисление токовой индуктивности в области 3 указывает на то, что она может быть управляема соотношением и направлением токов в центральной жиле и оплётке.
- При совпадении направлений обоих токов она мала и отрицательна. Её значение не может изменить положительный характер полной индуктивности коаксиального кабеля.
- При токах разных направлений эта часть индуктивности становится большой и может быть при одном отношении токов положительной, а при другом отношении токов – отрицательной.
- Численное моделирование для конкретных размеров областей показывает, что при определённых значениях противоположных токов индуктивность становится отрицательной и настолько большой, что знак полной индуктивности коаксиального кабеля тоже может стать отрицательным.
Рецензенты:
Бубнов В.А., д.т.н., профессор, заведующий кафедрой естественнонаучных дисциплин, ГБОУ ВПО «Московский городской педагогический университет», г. Москва;
Крутчинский С.Г., д.т.н., профессор кафедры систем автоматического управления, ФГАОУ ВПО «Южный федеральный университет», г. Ростов-на-Дону.
Работа поступила в редакцию 26.03.2014.