Восстановление функции распределения по выборке случайных данных, полученных в результате проведения тех или иных экспериментов, является основной задачей математической статистики [22], которая имеет важное практическое значение, например, при решении задач прочностной надежности элементов и объектов нефтегазового оборудования [44]. Обсуждаемая задача имеет следующую постановку: по экспериментальной выборке значений случайной величины Xi, 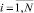 из генеральной совокупности найти функцию распределения F(y) = Pr{X ≤ y}, связанную с плотностью распределения f(y) интегральным соотношением
из генеральной совокупности найти функцию распределения F(y) = Pr{X ≤ y}, связанную с плотностью распределения f(y) интегральным соотношением
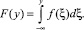 (1)
(1)
Известны два основных подхода к решению этой задачи: параметрический и непараметрический.
Параметрический подход предусматривает выбор на основе той априорной информации вида функции распределения случайной величины F(y), зависящей от некоторого набора параметров, и получении оценок их значений по имеющейся выборке данных, обеспечивающих максимальную близость теоретической функции распределения F(y) и эмпирической функции распределения
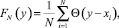 (2)
(2)
где функция Хэвисайда
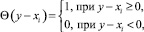
в соответствии с выбранной мерой близости, зависящей, вообще говоря, от вида распределения [55].
Существование решения обсуждаемой задачи обеспечивает центральная теорема математической статистики, согласно которой с ростом объема выборки N функция FN(y) с вероятностью, равной единице, равномерно приближается к F(y):
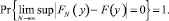
В основе непараметрической статистики лежит подход, позволяющий получать адаптивные оценки эмпирических распределений в виде некоторых функционалов, не зависящих от вида неизвестного априорного распределения [33]. Для восстановления неизвестной функции распределения в непараметрической статистике известен ряд методов и алгоритмов [33]: метод гистограмм, «гребенка», метод ближайших соседей, метод разложения по базисным функциям, аппроксимация Розенблатта ‒ Парзена и ряд других. Работоспособность методов непараметрической статистики и целесообразность их применения при анализе экспериментальных данных подтверждается результатами, полученными различными исследователями (см. список литературы, к разделу «Введение» в [33]). Например, в [44] показано, что аппроксимация Розенблатта ‒ Парзена оказывается весьма эффективной в задаче оценки долговечности нефте- и газопроводов на основе анализа накопленной статистической информации.
Результаты исследования особенностей аппроксимации Розенблатта ‒ Парзена в задаче аппроксимации одномодальных распределений дискретных и непрерывных случайных величин с ограниченной областью изложены в [66] и [77], соответственно.
В связи с тем, что на практике, например, при оценке прочностной надежности изделий [44] или анализе суточной выработки экскаваторов на горных работах [55] требуется получение оценок распределений случайных величин с двумодальными законами распределения, разработка методов оценки их параметров является актуальной задачей.
Напомним, что функция изучаемого распределения имеет две моды, каждая из которых имеет нормальный закон распределения с ограниченной областью рассеяния. Функция распределения выглядит следующим образом:
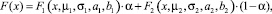 (3)
(3)
где μ1 – математическое ожидание первой составляющей; σ1 – математическое ожидание первой составляющей; a1, b1 – границы области рассеяния первой составляющей; μ2 – математическое ожидание первой составляющей; σ2 – математическое ожидание первой составляющей; a2, b2 – границы области рассеяния первой составляющей; α – доля первой составляющей в общем распределении.
Пример двумодальной функции распределения случайной величины, каждая мода которого имеет нормальный закон распределения с ограниченной областью рассеяния, представлен на рис. 1.
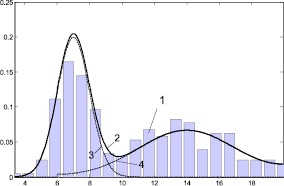
Рис. 1. Пример двумодального распределения: 1 – гистограмма случайной последовательности; 2 – плотность распределения случайной величины; 3 – график функции dF1(x, μ1, σ1, a1, b1)/dx; 4 – график функции dF2(x, μ2, σ2, a2, b2)/dx
Отметим, что в общем случае задача оценки параметров распределения сводится к решению той или иной системы нелинейных уравнений, для которых в подавляющем большинстве случаев приходится использовать соответствующие численные методы, например, итерационный метод Ньютона. Однако сходимость интеграционной последовательности к истинному решению оказывается очень сильно зависящей от выбора начального приближения. Вследствие этого в рассматриваемой задаче представляется перспективным использовать эвристические методы случайного поиска, результативность которых, как утверждается, не зависит от начального приближения и позволяет найти оптимальное решение при любых начальных условиях. Одним из таких методов являются генетические алгоритмы (ГА) [11].
В работе [88] была предложена методика совместного применения аппроксимации Розенблатта ‒ Парзена, метода мнимых источников и генетических алгоритмов в задаче оценки значений параметров распределений случайных последовательностей с двумодальными законами распределения вида (3), которая заключается в следующем:
1. Вычисление в соответствии с методом Розенблатта ‒ Парзена значений функции FRP(x), аппроксимирующей плотность распределения (3).
2. Вычисление оценок значений параметров 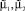 – абсцисс локальных максимумов функции FRP(x).
– абсцисс локальных максимумов функции FRP(x).
3. Вычисление оценки левой границы области рассеяния моды распределения (3), описываемой функцией 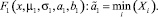
4. Вычисление оценки правой границы области рассеяния моды распределения (3), описываемой функцией 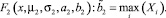
5. Вычислить, используя ГА, значения параметров σ1, b1, σ2, a2, α.
В результате проведенных экспериментов были определены оптимальные настройки ГА, а также была вычислена интегральная погрешность, значение которой позволило прийти к выводу о работоспособности данного метода.
Модифицированный метод оценивания параметров двумодального распределения
Отметим, что метод, описанный в [88], намеренно уменьшает размерность задачи для ГА, предварительно оценив параметры 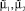 с помощью аппроксимации Розенблатта ‒ Парзена. Это было сделано вследствие того, что увеличение числа параметров значительно ухудшает результативность ГА. Поэтому ГА не производит поиск математического ожидания каждой из мод. Отсюда возникла идея модифицировать предложенный метод путем поэтапного попеременного нахождения меньшего числа параметров с помощью запуска ГА. В качестве начального приближения использовать результат предыдущего этапа. Таким образом, модифицированный метод оценивания параметров двумодального распределения реализуется следующей последовательностью действий:
с помощью аппроксимации Розенблатта ‒ Парзена. Это было сделано вследствие того, что увеличение числа параметров значительно ухудшает результативность ГА. Поэтому ГА не производит поиск математического ожидания каждой из мод. Отсюда возникла идея модифицировать предложенный метод путем поэтапного попеременного нахождения меньшего числа параметров с помощью запуска ГА. В качестве начального приближения использовать результат предыдущего этапа. Таким образом, модифицированный метод оценивания параметров двумодального распределения реализуется следующей последовательностью действий:
Этап 1. Вычисление в соответствии с методом Розенблатта ‒ Парзена значений функции FRP(x), аппроксимирующей плотность распределения (3). Наличие значений аппроксимирующей функции позволяет оценить примерный вид исходной функции распределения, а также получить оценки левой границы области рассеяния распределения (3), описываемой функцией F1(x, μ1, σ1, a1, b1):
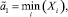
и правой границы области рассеяния распределения (3), описываемой функцией F2(x, μ2, σ2, a2, b2):
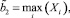
а также вычислить оценки значений параметров 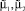 – абсцисс локальных максимумов функции FRP(x).
– абсцисс локальных максимумов функции FRP(x).
В связи с тем, что оценки параметров 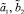 на данном этапе оказываются определенными достаточно точно, они на последующих этапах поиска принимались известными и их значения с помощью ГА не уточнялись.
на данном этапе оказываются определенными достаточно точно, они на последующих этапах поиска принимались известными и их значения с помощью ГА не уточнялись.
Этап 2. Вычисление с помощью ГА значений параметров σ1, b1, σ2, a2, α. (Здесь параметры μ1, μ2, оценки значений которых были оценены на предыдущем этапе по аппроксимации Розенблатта ‒ Парзена, считаются постоянными).
Этап 3. Вычисление с помощью ГА значений параметров μ1, b1, μ2, a2, α. (Здесь параметры σ1, σ2, оценки значений которых получены на этапе 2, считаются постоянными).
Этап 4. Вычисление с помощью ГА значений параметров σ1, σ2, α. (Здесь параметры μ1, b1, μ2, a, оценки значений которых получены на этапе 3, считаются постоянными, в качестве начального приближения параметров σ1, σ2, α используются значения, полученные на этапе 3).
Этап 5. Вычисление, используя ГА, значения параметров μ1, μ2. (Здесь параметры σ1, b1, σ2, a2, α, оценки значений которых получены на этапе 4, считаются постоянными, в качестве начального приближения параметров μ1, μ2 используются значения, полученные на этапе 4).
Этап 6. Вычисление, используя ГА, значения параметров σ1, σ2, α. (Здесь параметры μ1, b1, μ2, a, оценки значений которых получены на этапе 5, считаются постоянными, в качестве начального приближения параметров σ1, σ2, α используются значения, полученные на этапе 5).
Здесь в качестве целевой функции мы использовали интегральную погрешность вычисленной функции распределения по отношению к аппроксимации Розенблатта ‒ Парзена функции распределения случайной последовательности, полученной на этапе 1:
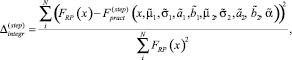 (4)
(4)
где 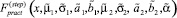 – функция распределения, полученная в результате запуска ГА на этапе
– функция распределения, полученная в результате запуска ГА на этапе 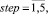 так как при ее вычислении использование данной целевой функции обусловлено тем, что не требуются значительные вычислительные ресурсы, а потому при ее использовании не происходит существенного увеличения времени работы ГА.
так как при ее вычислении использование данной целевой функции обусловлено тем, что не требуются значительные вычислительные ресурсы, а потому при ее использовании не происходит существенного увеличения времени работы ГА.
Из приведенного выше описания метода оценивания параметров двумодального распределения, видно, что на каждом этапе, начиная со второго, происходит уточнение значений параметров распределения, полученных на предыдущем этапе.
В ходе эксперимента предложенный метод был применен к двумодальным распределениям, параметры которых представлены в табл. 1.
Таблица 1
Параметры случайных двумодальных распределений
|
Параметры распределения |
μ1 |
σ1 |
a1 |
b1 |
μ2 |
σ2 |
a2 |
b2 |
α |
|
1 |
7 |
2 |
3 |
14 |
14 |
1 |
10 |
18 |
0,5 |
|
2 |
7 |
2 |
3 |
14 |
14 |
1 |
10 |
18 |
0,7 |
|
3 |
4 |
2 |
3 |
14 |
14 |
1 |
10 |
18 |
0,6 |
|
4 |
4 |
2 |
3 |
14 |
17 |
1 |
10 |
18 |
0,5 |
|
5 |
7 |
3 |
3 |
14 |
14 |
1 |
10 |
18 |
0,7 |
Для оценки качества методики использовалось значение погрешности, вычисляемое относительно теоретической функции распределения случайной последовательности:
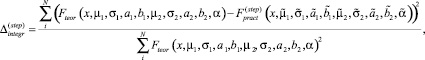
где 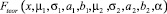 – теоретическая функция распределения.
– теоретическая функция распределения.
Результаты в виде графиков функций плотностей распределений и поэтапных интегральных погрешностей представлены на рис. 2–6.
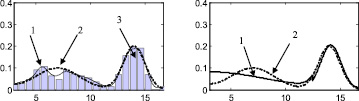
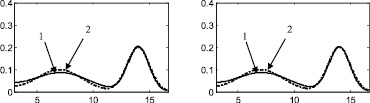
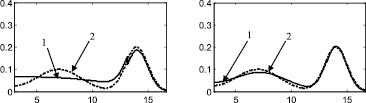
Стоит отметить, что итерационный метод является развитием двухэтапного метода, предложенного в [88] и также основанного на совместном использовании аппроксимации Розенблатта ‒ Парзена и метода мнимых источников. Таким образом, представляет интерес произвести сравнение итерационного метода с двухэтапным методом, а также с непараметрической аппроксимацией Розенблатта ‒ Парзена. Согласно описанию этапов итерационного метода, результат на первом этапе является аппроксимацией Розенблатта ‒ Парзена (рис. 2а, 3а, 4а, 5а, 6а), результат после второго этапа идентичен двухэтапному методу [88] (рис. 2б, 3б, 4б, 5б, 6б).
 б
б
 г
г
 е
е
 ж
ж
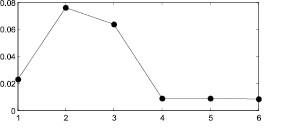
Рис. 2. Распределение 16: а – этап 1, б – этап 2, в – этап 3, г – этап 4, д – этап 5, е – этап 6, ж – поэтапная интегральная погрешность; 1 – экспериментальная функция плотности распределения, 2 – теоретическая функция плотности распределения, 3 – гистограмма выборки
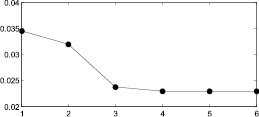
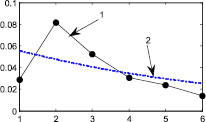
Из графиков на рис. 2ж–6ж видно, что функцию интегральной погрешности можно аппроксимировать функцией вида 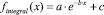 . Приведем значения коэффициентов a, b, c для каждого из рассмотренных распределений.
. Приведем значения коэффициентов a, b, c для каждого из рассмотренных распределений.
Графики представлены на рис. 7.
Из табл. 3 видно, что на седьмом этапе изменение погрешности становится несущественным и в предложенном итерационном методе можно ограничиться шестью этапами.
а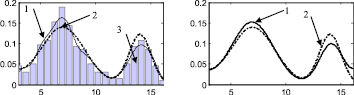 б
б
в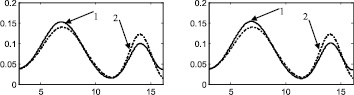 г
г
д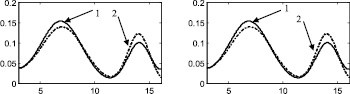 е
е
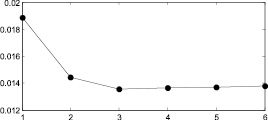 ж
ж
Рис. 3. Распределение 2: а – этап 1, б – этап 2, в – этап 3, г – этап 4, д – этап 5, е – этап 6, ж – поэтапная интегральная погрешность; 1 – экспериментальная функция плотности распределения, 2 – теоретическая функция плотности распределения, 3 – гистограмма выборки
Таблица 2
Параметры аппроксимирующих функций
|
Номер распределения |
a |
b |
c |
|
1 |
0,0642 |
0,2136 |
0,0002 |
|
2 |
0,0371 |
1,9481 |
0,0136 |
|
3 |
0,0245 |
0,5606 |
0,0213 |
|
4 |
0,0396 |
1,1779 |
0,0187 |
|
5 |
0,0654 |
0,1578 |
-0,0001 |
Таблица 3
Сравнение значений погрешностей на 6 и 7 шаге
|
Номер распределения |
finfegral(7) |
finfegral(7) – finfegral(6) |
|
1 |
0,0144 |
3,4264∙10-3 |
|
2 |
0,0137 |
2,6731∙10-7 |
|
3 |
0,0218 |
3,6310∙10-4 |
|
4 |
0,0187 |
2,3297∙10-5 |
|
5 |
0,0217 |
3,7045∙10-3 |
а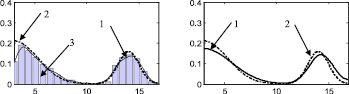 б
б
в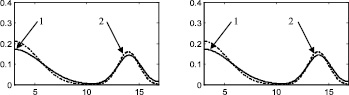 г
г
д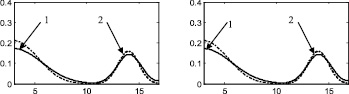 е
е
 ж
ж
Рис. 4. Распределение 3: а – этап 1, б – этап 2, в – этап 3, г – этап 4, д – этап 5, е – этап 6, ж – поэтапная интегральная погрешность; 1 – экспериментальная функция плотности распределения, 2 – теоретическая функция плотности распределения, 3 – гистограмма выборки
Таким образом, полученные результаты позволяют сделать вывод о том, что предложенная методика в целом показывает результат лучший, чем двухэтапный метод и метод Розенблатта ‒ Парзена. С каждым следующим этапом предложенного метода оценки параметров двумодальных распределений наблюдается тенденция к уменьшению интегральной погрешности. При этом, начиная с 6 этапа, изменение значения интегральной погрешности становится уже несущественным, поэтому можно утверждать, что для получения оптимального результата вполне достаточно 6 этапов.
Выводы
Анализ результатов совместного применения аппроксимации Розенблатта ‒ Парзена и итерационного метода мнимых источников и генетических алгоритмов в задаче оценки значений параметров распределений случайных последовательностей с двумодальными законами распределения вида (3), относящегося к классу 9-ти параметрических распределений, позволяет сделать следующие выводы:
а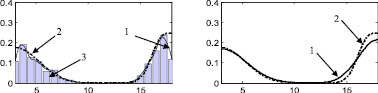 б
б
в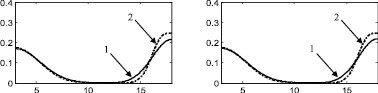 г
г
д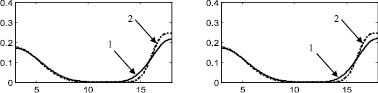 е
е
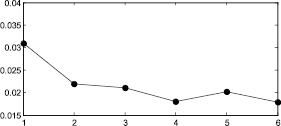 ж
ж
Рис. 5. Распределение 4: а – этап 1, б – этап 2, в – этап 3, г – этап 4, д – этап 5, е – этап 6, ж – поэтапная интегральная погрешность; 1 – экспериментальная функция плотности распределения, 2 – теоретическая функция плотности распределения, 3 – гистограмма выборки
1. Предложен модифицированный метод нахождения параметров изученного двумодального распределения случайных последовательностей, основанный на совместном использовании аппроксимации Розенблатта ‒ Парзена и ГА, и получено подтверждение ее работоспособности.
2. Проведены вычислительные эксперименты, подтверждающие эффективность предложенного метода оценивания параметров двумодального распределения.
3. Получены оценки точности нахождения параметров распределения в виде интегрального показателя, характеризующего в целом качество оценки плотности распределения случайной последовательности с изученным законом распределения.
а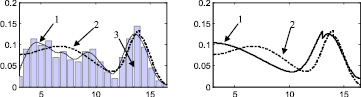 б
б
в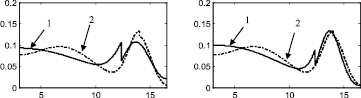 г
г
д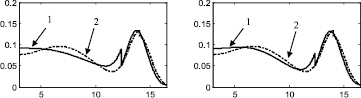 е
е
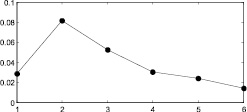 ж
ж
Рис. 6. Распределение 5: а – этап 1, б – этап 2, в – этап 3, г – этап 4, д – этап 5, е – этап 6, ж – поэтапная интегральная погрешность; 1 – экспериментальная функция плотности распределения, 2 – теоретическая функция плотности распределения, 3 – гистограмма выборки
а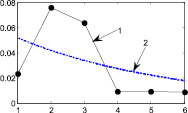
 б
б
в 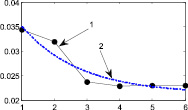 в
в 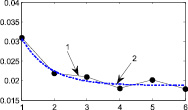 г
г
 д
д
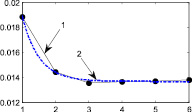
Рис. 7. 1 – поэтапная интегральная погрешность, 2 – аппроксимация функцией вида 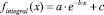 : а–д – распределения 1–5 соответственно Получив аппроксимацию интегральной погрешности, можно вычислить погрешность на следующем седьмом шаге итерационного метода и сравнить ее с предыдущим шестым шагом
: а–д – распределения 1–5 соответственно Получив аппроксимацию интегральной погрешности, можно вычислить погрешность на следующем седьмом шаге итерационного метода и сравнить ее с предыдущим шестым шагом
Рецензенты:
Кубланов В.С., д.т.н., доцент, профессор кафедры радиоэлектроники информационных систем, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой информационных технологий, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 26.03.2014.



