В настоящее время в мире интенсивно расширяется область использования летающих мультиротационных роботов, способных нести информационную полезную нагрузку в виде видеоаппаратуры которые для успешного выполнения задач мониторинга окружающей среды должны обладать высокой маневренностью, быстродействием и точностью движения по заданным траекториям, [3, 5]. Вопросам монтажа навесного оборудования на квадрокоптере ведущие разработчики и производители уделяют значительное внимание, так как параметры и динамическое качество кронштейнов подвески существенно влияют на качественные показатели изображения объектов мониторинга. Определение параметров системы подвески можно осуществить, анализируя с помощью математической модели движение навесного оборудования в пространстве относительно объектов мониторинга.
Рассмотрим математическую модель, описывающую движение навесного оборудования. Будем считать, что навесное оборудование моделируется материальной точкой массой m. Обозначим эту точку буквой В. Пусть навесное оборудование закреплено на квадрокоптере с помощью трехкоординатной упруго-вязкой подвески так, как это изображено на рис. 1, 2.
Точка В0 в связанной с коптером системе координат определяет начальное положение навесного оборудования. Пусть вектор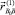 
определяет положение массы m в произвольном положении относительно В0:
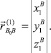(1)
Радиус-вектор, определяющий положение точки В0:
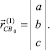(2)
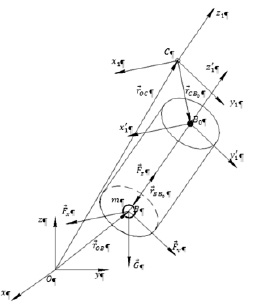
Рис. 1. Расчетная схема движения навесного оборудования
На массу m действуют сила веса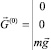 
, направленная параллельно оси Oz неподвижной системы координат, и силы 
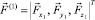, вызванные деформацией упруго-вязкого элемента по осям связанной системы координат.
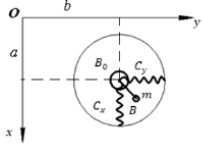
Рис. 2. Определения произвольного положения навесного оборудования в горизонтальной плоскости
Рассмотрим движение массы m в системе координат Oxyz. Пусть положение точки B в этой системе координат определяет вектор:
(3)
Для обеспечения качественной видеосъемки окружающей среды, с которой связана неподвижная система координат, необходимо свести к минимуму вибрацию навесного оборудования относительно этой системы координат. Пусть навесное оборудование моделируется материальной точкой массой m. Дифференциальное уравнение движения точки B в неподвижной системе координат имеет вид:
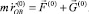(4)
Для определения ускорения точки B запишем равенство:
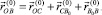(5)
Точка B0 соответствует положению точки B в недеформированном состоянии упруго-вязкого элемента.
Определим:
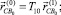
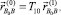(6)
где T10 – матрица поворота системы Cx1y1z1 относительно Oxyz.
Тогда равенство (5) принимает вид:
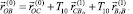(7)
Положение точки B в связанной системе координат определяется тремя параметрами, образующими вектор:
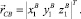(8)
Тогда в проекциях выражение (7) имеет вид:
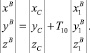(9)
Деформация упруго-вязких элементов определяется по формулам:
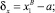
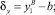
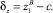
Силы, действующие на материальную точку без учета вязких слагаемых, определяются по формулам:
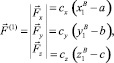(10)
где сx, сy, сz – приведенные жесткости подвеса по соответствующим координатам. Если конструкция подвесного кронштейна разработана и изготовлена, то определение этих параметров возможно как теоретическими методами с использованием метода конечных элементов, так и экспериментальными. В этом случае важно исследовать характер движения навесного оборудования установленного на подвесе с этими параметрами. В том случае, когда проектируется новая система подвеса, желательно разработать метод синтеза коэффициентов жесткости подвески по критериям минимума отклонения навесного оборудования от заданного положения.
Продифференцировав дважды (7) и подставив (4) получим:
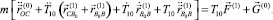(11)
С учетом (8) запишем (11) в проекциях на координатные оси Oxyz:
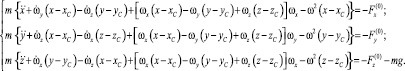(12)
Данная система уравнений описывает движение установленного на квадрокоптере навесного оборудования в режиме съемки объектов, расположенных в неподвижной системе координат.
Найдем силы, действующие на навесное оборудование со стороны кронштейна подвески F(0) в неподвижной системе координат:
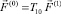
или
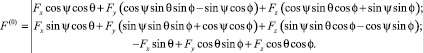
Будем считать, что масса навесного оборудования значительно меньше массы квадрокоптера. Поэтому колебания навесного оборудования не оказывают влияния на характер движения коптера.
Сформулируем задачу следующим образом. Пусть известные функции xC(t), yC(t), zC(t), ωx(t), ωy(t), ωz(t), φ(t), ψ(t), θ(t), полученные в результате интегрирования системы уравнений описывают движение квадрокоптера.
Определим функции x(t), y(t), z(t) путем интегрирования системы дифференциальных уравнений (12).
Ниже приведены некоторые результаты полученные при моделировании движения навесного оборудования, установленного на квадрокоптере, в режиме зависания в предположении, что частоты внешнего воздействия по координатным осям равны.
Анализ полученных диаграмм показывает, что при определенных частотах происходит резкое увеличение амплитуды колебаний навесного оборудования. Этот факт необходимо учитывать при проектировании кронштейна подвески. Оптимальным является отношение частот внешнего воздействия и собственных частот в диапазоне 3–5.
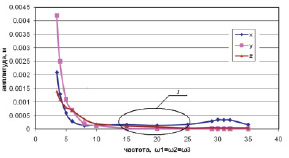
Рис. 3. Амплитудо-частотная характеристика: 1 – область рациональных параметров
Для определения конструктивных параметров кронштейна подвеса навесного оборудования использована методика расчета, основанная на программном комплексе SolidWorks.
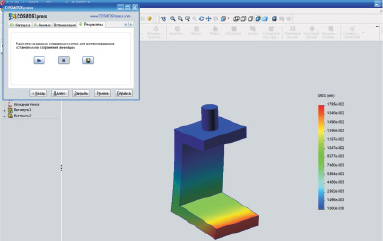
Рис. 4. Схема деформации кронштейна в вертикальном направлении
Некоторые результаты расчетов параметров проектируемого кронштейна представлены на рис. 4, 5. Основная задача, которая решалась при этом, состояла в определении жесткости кронштейна по трем координатам в зависимости от вида материала, из которого он изготовлен, и геометрических размеров.
В основе методики лежит метод зондирования пространства варьируемых параметров, определяемых вектором 
, 
. В качестве критерия качества принимаем безразмерное отклонение жёсткости кронштейна по соответствующей оси от заданного значения. Далее решается задача аппроксимации точек гладкой поверхностью второго порядка. На этой поверхности находим минимум K(b*), где b* – вектор параметров, приводящий критерий K к минимуму. В качестве варьируемых параметров выступают геометрические размеры кронштейна.
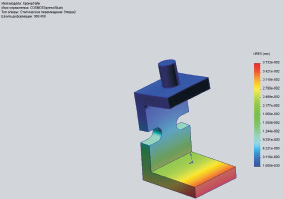
Рис. 5. Схема деформации кронштейна с вырезами в горизонтальном направлении
В расчетах рассматривались схемы деформации кронштейна в вертикальном и горизонтальном направлении. В том числе исследовалось влияние геометрической формы кронштейна, в том числе вырезы на вертикальной полке кронштейна.
Выводы
Разработана математическая модель, описывающая пространственное движение навесного оборудования установленного на упруго-вязком подвесе. В результате математического моделирования установлена зависимость амплитуды колебаний по трем координатам и частотой внешнего периодического воздействия для заданных параметров упруго-вязкого подвеса. Установлено наличие резонансного эффекта, связанного со значительным увеличением амплитуды колебаний при приближении возмущающей частоты к критическим частотам.
Рецензенты:
Локтионова О.Г., д.т.н., доцент, проректор по учебной работе, ФГБОУ ВПО «Юго-Западный государственный университет», г. Курск;
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ФГБОУ ВПО «Юго-Западный государственный университет», г. Курск.
Работа поступила в редакцию 26.03.2014.