Опыт ранее проведенных подобных исследований [1, 2, 3 и т.д.] показал, что достоверность и практическая ценность результатов моделирования полей температур, напряжений и деформаций в деталях двигателей внутреннего сгорания (ДВС) с применением метода конечных элементов (МКЭ) и других расчетных методов определяется, в первую очередь, наличием научно-обоснованных методов выбора и правильности определения закладываемых в расчеты граничных условий (ГУ). Это в равной степени относится к теплонагруженным оребренным цилиндрам всех машин.
Определение граничных условий
В качестве основных ГУ, описывающих тепловое взаимодействие поверхностей деталей и окружающей среды, используют следующие их виды (для цилиндрической системы координат) [7]:
– ГУ 1-го рода (задано распределение температур по поверхности детали в любой момент времени):
t = t(r, z, Θ, τ), (1)
где t(r, z, Θ, τ) – заданная на поверхности тела функция температуры; r, z, Θ – цилиндрические координаты; τ – координата времени;
– ГУ 2-го рода (задана плотность теплового потока (q) через поверхность):
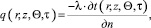(2)
где n – нормаль к поверхности детали в точке с координатами r, z, Θ; l – коэффициент теплопроводности материала детали, Вт/(м⋅град);
– ГУ 3-го рода (задана температура окружающей среды (toc) и закон теплообмена между средой и поверхностью):
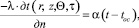(3)
где a – коэффициент теплоотдачи для поверхности детали, Вт/(м2×град);
– ГУ 4-го рода (задан теплообмен системы тел, происходящий по закону теплопроводности):
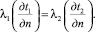(4)
Наибольшая достоверность прогнозируемых полей температур, деформаций и напряжений достигается при использовании ГУ 3-го рода, так как они наиболее стабильны при изменении конструкции деталей. Как показал анализ ранее проведенных исследований [1, 2, 4, 7 и т.д.], допущение стабильности ГУ 3-го рода при этом вполне отвечает запросам инженерной практики. В свою очередь ГУ 3-го рода непосредственно зависят от параметров рабочего процесса, характера и особенностей смесеобразования, сгорания и тепловыделения, поэтому они наиболее полно и правильно отражают физическую природу теплообмена в цилиндре ДВС. При моделировании изменений конструкционных параметров тепло нагруженных деталей машин ГУ 3-го рода относительно стабильны, что позволяет производить оптимизацию конструкций деталей путем численных вариантных исследований.
Использование других ГУ оправдано только в случае необходимости получения распределения температур в теле исследуемой детали по известным их значениям на поверхностях.
Вследствие недостаточной изученности вопроса определения ГУ 3-го рода для цилиндров ДВС с воздушным охлаждением возникла необходимость в систематизации имеющейся в литературе информации по данному вопросу и разработке соответствующей практичной и эффективной методики определения ГУ [4, 5, 6]. В известной авторам литературе подобной методики нет.
С целью обеспечения универсальности подхода в качестве базовой информации должны использоваться экспериментальные значения температур в характерных точках цилиндров и температур окружающих сред для их теплоотводящих и теплоподводящих участков теплообмена.
Предлагаемая методика определения ГУ 3-го рода для оребренных цилиндров ДВС базируется на аналитических зависимостях теплопередачи через ребристые поверхности, полученных на основе законов теплопередачи Фурье и Ньютона [4, 6].
Для локализации ГУ по рабочей длине цилиндра его теплоподводящая и теплоотводящая поверхности разделены на участки равного теплообмена. При этом введено понятие кольцевого пояса цилиндра, образованного перпендикулярными оси цилиндра сечениями по границам участков. Каждому i-поясу соответствует теплоподводящий i-участок и теплоотводящий (i + m)-участок цилиндра при количестве кольцевых поясов m.
Упрощенная расчетная схема оребренного цилиндра ДВС для разработки конечно-элементных моделей (КЭМ) их температурного состояния с сеткой конечных элементов (КЭ) приведена на рисука. Допущено, что теплообмен между кольцевыми поясами незначителен и может не учитываться.
Значения определяющих температур окружающих сред tосi для участков теплообмена зеркала цилиндра определяются на базе диаграммы мгновенных значений температур газов в цилиндре.
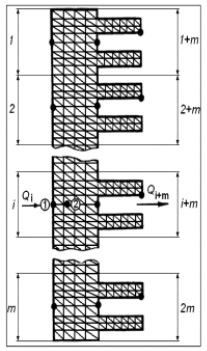
Расчетная схема оребренного цилиндра: i = 1…2m – участки теплообмена; ● – узлы сетки КЭ, соответствующие характерным точкам участков
Для верхних зон зеркала цилиндра до места остановки верхнего компрессионного кольца (ВКК) поршня в верхней мертвой точке (ВМТ) за tосi принимается средняя результирующая температура газов в цилиндре. Для тепловоспринимающих участков зеркала цилиндра, находящихся ниже положения ВКК в ВМТ, назначение tосi производится с учетом отсутствия воздействия горячих газов на них в течение отдельных периодов работы двигателя, когда указанные зоны перекрыты поршнем от очага сгорания [5]. Это следует производить на базе индикаторной диаграммы двигателя, снятой одновременно с оценкой температур в точках цилиндра. Данные вычисления не составляют труда для специалиста.
В дальнейшем полученные значения tосi по необходимости корректируются для каждого участка поверхности с учетом дополнительного подвода теплоты через поршневые кольца и отводимой через цилиндр теплоты трения [2, 7].
Значения определяющих температур окружающих сред для теплоотводящих участков теплообмена оребренного цилиндра t ос(i+m) назначаются на основе экспериментальной оценки температуры охлаждающего воздуха в межреберных каналах, что не вызывает особых практических трудностей.
Для i-пояса коэффициент теплопередачи αi на теплоподводящем i-участке с площадью Si определяется с использованием допущения о равенстве количества тепла, подводимого к рассматриваемому участку Qi и отводимого от его поверхности теплопроводностью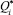 
:
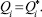(1)
Величины Qi и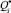 
определяются по выражениям [73, 293, 402]:
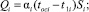(2)
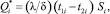(3)
где t1i и t2i – температуры соответственно в характерной точке i-участка и в точке на глубине δi по нормали к поверхности, °С; λ – коэффициент теплопроводности материала цилиндра, Вт/(м·град).
После подстановки (2) и (3) в (1) и проведения несложных математических вычислений получена формула определения величин коэффициентов αi для теплоподводящих участков цилиндра:
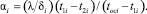(4)
Следует учесть, что формула (4) является приближенным выражением закона теплопроводности Фурье [4, 6]. Полное соответствие закона Фурье и выражения (4) наблюдается в случае одномерных, стационарных температурных полей с параллельными изотермическими поверхностями и в однородных средах. В реальных условиях работы ДВС имеет место не одномерность полей температур цилиндра, не стационарность температурного поля, неоднородность материалов, что приводит к определенному рассогласованию выражения (4) и закона Фурье. Для достижения наибольшего соответствия, очевидно, следует стремиться к максимальному уменьшению δi. Как следствие, чем меньше δi, тем более правильно отвечает полученное по формуле (4) значение αi реальной величине.
Вместе с тем осуществление эксперимента по оценке температур точек при стремлении δi к нулю практически труднодостижимо, поэтому для получения значений температур t2i необходимо проведение отдельного анализа температурного состояния цилиндров с использованием МКЭ и ГУ 1 рода. В свою очередь, ГУ 1-го рода могут быть получены на базе экспериментальных значений температур в характерных точках поверхностей цилиндров путем интерполяции между экспериментальными точками. За t2i при этом берутся значения температур в узлах сетки КЭ, соседних по нормали к поверхности с характерными точками тепловоспринимающих участков, а за δi – соответствующее расстояние между узлами сетки (рисунок).
Результаты исследования и их обсуждение
Из всех существующих методов экспериментального определения температур деталей ДВС для решения задач данного исследования наиболее приемлемы [3, 6]:
- метод пироскопии, основанный на применении сплавов и чистых металлов с определенной температурой плавления;
- метод, основанный на изменении твердости некоторых металлов при различных степенях нагрева;
- метод измерения температур с применением кристаллических измерителей;
- термоэлектрические методы, предусматривающие использование термопар или термосопротивлений.
Представленная методика предполагает установление датчиков (термопар, термосопротивлений, металлопроб с изменяемой температурой плавления или твердостью и т.д.) для измерения температур цилиндров в местах, соответствующих узлам сетки КЭ по характерным точкам участков теплообмена. Авторы данной работы для подобных исследований используют термометрический метод с применением термопар. К основным преимуществам термоэлектрических методов следует отнести возможность анализа температур при изменении режимов работы двигателей [3].
Следует отметить, что при увеличении количества введенных условно кольцевых поясов теплообмена цилиндров адекватность КЭМ температурного состояния будет возрастать. Однако это как раз ограничивается особенностями экспериментальной оценки температур. Размещение большого количества любых датчиков искажает реальную картину теплового состояния цилиндров. Например, установка термопар предполагает предварительные сверления; материал датчиков заведомо инородный материал, в сравнении с материалом цилиндров и т.д.
Для различных расчетно-теоретических исследований допустимо принимать постоянные значения коэффициентов теплоотдачи для теплоотводящих участков αi+m по высоте ребер охлаждения цилиндров, что упрощает процессы расчетов при получении достаточной для практических целей точности.
В первом приближении для i-пояса цилиндра коэффициент теплоотдачи αi+m на оребренном (i+m)-участке с площадью S i+m определен из условия равенства количества подводимого к участку и отводимого от него в охлаждающий воздух тепла:
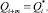(5)
где Qi+m – количество тепла, отводимого в охлаждающую среду от оребренной поверхности (i + m)-участка.
После предварительного определения температуры t ос(i+m) для теплоотводящего (i+m)-участка цилиндра (замер температуры охлаждающего воздуха) и средней температуры поверхности tср(i+m) (по экспериментальным значениям температур в характерных точках поверхности охлаждения) вычисляется количество тепла:
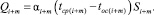(6)
В результате подстановки (3) и (6) в (5) и некоторых математических преобразований получено выражение для приближенного определения значений коэффициентов теплоотдачи αi+m для теплоотводящих участков оребренных цилиндров ДВС с воздушным охлаждением:
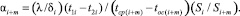(7)
Приближенность формулы (7) объясняется условностью принятого допущения об отсутствии теплообмена между кольцевыми поясами, т.е. о равенстве Qi и Qi+m, а также тем, что в результате вычисляется среднее значение коэффициента теплоотдачи для оребренной поверхности теплоотводящего участка без учета изменения его по высоте ребра охлаждения. Таким образом, при использовании данной методики на практике может возникнуть необходимость в корректировке значений αi+m для достижения требуемого соответствия расчетных и экспериментальных значений температур в контрольных точках участков теплообмена оребренных цилиндров ДВС. Рекомендуется при этом производить корректировку величин коэффициентов теплоотдачи на теплоотводящих участках в силу большей приближенности их определения, в сравнении с теплоподводящими участками. На данном этапе, к тому же, может быть задан любой закон распределения αi+m по поверхностям ребер охлаждения.
Выводы
Проведенные исследования показали:
- адекватность математических моделей теплонапряженности деталей ДВС в наибольшей степени зависит от правильности задания граничных условий при моделировании;
- для моделирования температурных полей цилиндров ДВС с воздушным охлаждением весьма эффективна представленная расчетно-экспериментальная методика определения граничных условий 3 рода;
- исходной информацией для моделирования являются значения температур в характерных точках оребренных цилиндров, которые рекомендуется получать термоэлектрическим экспериментом;
- результаты исследований должны учитываться и использоваться специалистами, занимающимися проектированием и доводкой ДВС с воздушным охлаждением.
Рецензенты:
Панов А.Ю., д.т.н., профессор, директор ИПТМ, Нижегородский государственный технический университет им. Р.Е. Алексеева, г. Нижний Новгород;
Молев Ю.И., д.т.н., профессор кафедры «Строительные и дорожные машины», Нижегородский государственный технический университет им. Р.Е. Алексеева, г. Нижний Новгород.
Работа поступила в редакцию 26.03.2014.