В работах [2, 4–6] мы исследовали возможности обобщения представлений о структуре пространства и времени на основе выдвинутой нами гипотезы об иерархической гиперконтинуальной структуре мирового физического пространства-времени. Подтверждение гипотезы откроет принципиально новые горизонты развития научно-технического прогресса, ранее казавшиеся недостижимыми, сняв ограничения отдельного континуума (ограниченность скорости движения скоростью света в вакууме, жесткость причинно-следственных цепочек событий и т.д.). Но иерархичность гиперконтинуума ограничивает применимость общепринятого принципа геометризации в физике и связанных с ним идей симметрии в геометрии за счет введения в теоретическую физику идей иерархичности, эффективность которых уже апробирована нами в рамках информатики при создании эталонной модели защищенной автоматизированной системы (ЭМЗАС) и математического аппарата ЭМЗАС-сетей [3].
Целью настоящей работы является критический обзор изложенных в научной литературе идей симметрии при описании пространства-времени на основе принципа геометризации.
Вопрос о связи свойств пространства и времени со свойствами движения материи обсуждается в научной литературе, начиная с работ А. Пуанкаре. В [9] он резюмировал свои рассуждения по теме правил измерения времени так: «Одновременность двух событий или порядок их следования, равенство двух длительностей должны определяться таким образом, чтобы формулировка естественных законов была бы настолько простой, насколько это возможно. Другими словами, все эти правила, все эти определения являются лишь плодом неосознанного соглашения». В [12] Пуанкаре пришел к выводу:
«1. Абсолютного пространства не существует, мы знаем только относительные движения. Между тем чаще всего выражают механические факты так, как если бы существовало абсолютное пространство, к которому их можно было бы отнести.
2. Не существует абсолютного времени. Утверждение, что два промежутка времени равны, само по себе не имеет смысла, и можно применять его только условно.
3. Мы не способны к непосредственному восприятию не только равенства двух промежутков времени, но и не можем быть уверенными в одновременности двух событий, происходящих в различных местах. (Я пояснил это в статье [9].)
4. Наконец, сама наша евклидова геометрия – лишь своего рода условный язык.
Мы могли бы изложить факты механики, относя их к пространству неевклидову, которое было бы основой менее удобной, но столь же законной, как и наше обыкновенное пространство. Изложение слишком осложнилось бы, но осталось бы возможным. Таким образом, абсолютное пространство, абсолютное время, даже сама геометрия не имеют характера вещей, обусловливающих собой механику. Они так же мало предваряют существование механики, как мало французский язык логически предваряет существование истин, выражаемых по-французски».
Итак, А. Пуанкаре пришел к выводу о том, что структура времени самого по себе и пространства самого по себе являются предметом соглашения и могут быть выбраны произвольными, хотя, возможно, и осложняющими описание. Но впоследствии А. Пуанкаре показал в [11], что пространство и время сами по себе более относительны, чем некоторое их соединение в единое пространство-время, абсолютизм которого еще может иметь какой-то смысл.
О важности этих идей Г. Лоренц писал [7]: «… Пуанкаре получил полную инвариантность уравнений электродинамики и сформулировал «постулат относительности» – термин, впервые введенный им. … Он не ограничился показом того, что релятивистские преобразования оставляют неизменной форму электромагнитных уравнений. Он объясняет успех подстановок тем, что эти уравнения могут быть представлены в форме принципа наименьшего действия, и что фундаментальное уравнение, выражающее этот принцип, а также операции, с помощью которых выводятся уравнения поля, одинаковы в системах x, y, z, t и x′, y′, z′, t′ … «Группа относительности», получаемая таким образом, состоит из линейных подстановок, не нарушающих квадратичную форму x2 + y2 + z2 – t2. … при рассмотрении x, y, z и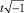 
как координат точки в четырехмерном пространстве релятивистские преобразования сводятся к вращениям в этом пространстве. … Напоминаю об этих идеях Пуанкаре потому, что они близки к тем методам, которыми пользовались позже Минковский и другие ученые для облегчения математических действий, встречающихся в теории относительности».
По-видимому, эти идеи Пуанкаре явились важным поворотным пунктом в истории теоретической физики, дав удобный повод к торжеству принципа геометризации, который, на наш взгляд, является сегодня одним из важнейших факторов, сдерживающих ее развитие. Пространство и время имеют разный физический смысл, но их оказалось возможным рассматривать в рамках единой геометрической структуры, претендующей на роль одной из абстрактных идей, лежащих в основе мира конкретных материальных вещей. Это отражало давние, еще со времен древнегреческого философа Платона, чаяния европейского идеалистического мировоззрения, которое веками ждало своего звездного часа в естествознании. Про вклад Платона в формирование этого мировоззрения Ш. Яу и С. Надис написали: «он не только понял, что математика является ключом к познанию Вселенной, но и продемонстрировал подход, который называется геометризацией физики, – аналогичный прорыв сделал Эйнштейн. В порыве предвидения Платон предположил, что элементы природы, их качества и действующие между ними силы могут быть результатом воздействия скрытой от нас колоссальной геометрической структуры. Видимый нами мир вполне может оказаться всего лишь отражением лежащей в его основе геометрии, недоступной для нашего восприятия» [16].
Начиная с великого геометра Пуанкаре, к теоретической физике приобщились многие другие геометры, оказавшие глубокое влияние на ее развитие в направлении все большей геометризации. Но мотивация исследований геометров другая, чем физиков: «Геометров больше всего восхищают мощь и красота абстрактных принципов, лежащих в основе очертаний и форм объектов окружающего мира» [16]. Можно особо подчеркнуть, что геометров восхищает не движение объектов, а их форма. Коротко говоря, «геометризация – идея, что физика, которую мы наблюдаем, вытекает непосредственно из геометрии» [16].
Пуанкаре, хотя и передал физике импульс к ее геометризации, еще не придавал геометрии единого пространства-времени определяющего значения. Важный шаг в этом направлении сделал Г. Минковский, который в [8] написал: «Воззрения на пространство и время … возникли на экспериментально-физической основе. В этом их сила. Их тенденция радикальна. Отныне пространство само по себе и время само по себе должны обратиться в фикции, и лишь некоторый вид соединения обоих должен еще сохранить самостоятельность. …Попытку перешагнуть через понятие пространства соответствующим образом в самом деле можно было бы расценить как некоторую дерзость математической мысли. Но после такого все-таки неизбежного шага для истинного понимания группы Gc термин «постулат относительности» для требования инвариантности по отношению к группе Gc кажется мне слишком бледным. Так как смысл постулата сводится к тому, что в явлениях нам дается только четырехмерный в пространстве и времени мир, но что проекции этого мира на пространство и на время могут быть взяты с некоторым произволом, мне хотелось бы этому утверждению скорее дать название «постулат абсолютного мира» (или, коротко, мировой постулат)».
Минковский уже явно признавал за геометрией единого пространства-времени определяющую роль для физики, о чем свидетельствуют его слова: «Мне хочется верить, что не имеющая исключений справедливость мирового постулата является истинной основой электромагнитной картины мира, основой, которая была найдена Лоренцем, очищена далее Эйнштейном и которая теперь предстала пред нами во всей ясности» [8]. Для такой роли геометрии Минковский подобрал философское обоснование в духе платонизма: «При дальнейшей разработке математических следствий найдется достаточно указаний для экспериментальной проверки истинности постулата для того, чтобы примирить с ним, на основе идеи о предустановленной гармонии между чистой математикой и физикой, и тех, которым неприятно или больно оставить привычные воззрения» [8]. Это философское обоснование геометризации физики господствует до сих пор, о чем написал В.П. Визгин в [1]: «уверенность теоретиков в существовании «предустановленной гармонии между физической природой и математическим образом мышления» (выражение Г. Вейля) или даже вера в нее была и остается одним из важнейших факторов построения фундаментальных физических теорий».
Именно в псевдоевклидовости геометрии пространства-времени видел суть специальной теории относительности Минковский [8]. Но Эйнштейн не придавал геометрии пространства-времени фундаментальной роли в ней, определяя эту геометрию как следствие более фундаментальных (на его взгляд) физических положений: заимствованного у Пуанкаре [10] принципа относительности и постулата о постоянстве скорости света в вакууме. Тем не менее Эйнштейн увидел в геометрическом представлении Минковского красоту и наглядность, вдохновившие его на еще большее усиление роли геометрии пространства-времени в общей теории относительности. Сам Эйнштейн написал по этому поводу следующее: «Даже нематематику должно быть ясно, что благодаря этому чисто формальному положению теория относительности чрезвычайно выиграла в наглядности и стройности. Эти краткие указания дают читателю лишь смутное представление о важных мыслях Минковского, без которых общая теория относительности, … быть может, оставалась бы в зачаточном состоянии» [14].
После создания Лоренцем, Пуанкаре, Эйнштейном и Минковским специальной теории относительности возникла ситуация, хорошо описанная Р. Фейнманом в [13]: «Физика в большой степени состояла из теории гравитации и электродинамики, и именно электродинамика вызвала к жизни создание теории относительности, так что проблема состояла в том, чтобы внести теорию гравитации в общую канву открытий, сделанных при изучении электродинамики». При решении этой проблемы Эйнштейн придерживался согласующегося с идеями Минковского мнения относительно выбора геометрии единого пространства-времени: «… вопрос о том, имеет этот континуум евклидову, риманову или какую-либо другую структуру, является вопросом физическим, ответ на который должен дать опыт, а не вопросом соглашения о выборе на основе простой целесообразности» [15]. Но Эйнштейн отошел от теоретико-полевого подхода, которому, вслед за Фарадеем и Максвеллом, продолжали следовать Лоренц, Пуанкаре и Минковский, и согласно которому любое физическое поле, в том числе гравитационное, является материальным объектом, активно движущимся в пространстве-времени, а не пассивным проявлением каких-то геометрических его свойств. Подход Эйнштейна означал вытеснение теоретико-полевого подхода геометризацией.
Ситуация после создания общей теории относительности по [13]: «Эйнштейновская теория гравитации, которая, как утверждается, явилась величайшим открытием в теоретической физике, заключается в красивых соотношениях, связывающих гравитационные эффекты с геометрией пространства, что было довольно увлекательной идеей. Видимая простота гравитационных и электрических сил, например, состоящая в том, что и те, и другие следуют закону обратных квадратов, который может понять любой ребенок, приводит к тому, чтобы у каждого из этих «детей» появилась мечта о том, что когда он подрастет, он найдет дорогу к геометризации электродинамики. Таким образом, поколения физиков делали попытки создания так называемых единых теорий поля, которые могли бы объединить гравитацию и электродинамику в рамках единой теории. Ни одна из созданных теорий не была успешной… Большая часть из этих теорий являлась просто математическими игрушками, создаваемыми математически мыслящими людьми, у которых было довольно слабое знание физики, большая часть из этих теорий непонимаема. Сам Эйнштейн также работал над этими теориями, и его сочинения на эту тему, по крайней мере, имеют некоторый смысл, тем не менее успешной теории поля, которая бы объединяла гравитацию и электродинамику, не существует».
Действительно ли дальнейшее обобщение представлений о пространстве и времени лежит в русле геометризации электродинамики? Сам Фейнман выражал некоторый скепсис: «В случае создания подобной единой теории такой успех был бы кратковременным, поскольку в настоящее время в физике заключено существенно больше, чем только электродинамика и гравитация, и нам нужно было бы побеспокоиться об объединении мезонов, каонов и нейтрино и всех других тридцати и более элементарных частиц, которые сейчас известны. Таким образом, подобное объединение электродинамики и гравитации не было бы таким великим достижением, как это представлялось ранее, поскольку в мире есть много другого, кроме электричества и гравитации» [13]. Так что геометризовывать нужно слишком многое.
Несмотря на очевидную трудоемкость такой всеобъемлющей геометризации, она оказалась чрезвычайно заманчивой для «математически мыслящих людей» (по выражению Фейнмана) с близким платонизму мировоззрением. Выдающийся их представитель Ш. Яу писал по поводу своих собственных интересов такого рода следующее: «Я был поражен тем, что гравитационные эффекты и искривление пространства могут рассматриваться как одно и то же, ведь криволинейные поверхности очаровали меня еще в первые годы обучения в Гонконге. Что-то в этих формах привлекло меня на интуитивном уровне. …Информация о том, что кривизна лежит в основе общей теории относительности Эйнштейна, наполнила меня надеждой в один прекрасный день внести свой вклад в наше понимание Вселенной» [16].
С господствующей в теоретической физике точки зрения ее геометризации в духе платоновского идеализма значение соответствующих идей Платона и оценка перспектив понимания физических законов Вселенной определены Ш. Яу и С. Надисом в [16]: «Платон совершенно верно предположил, что в основе любого правдоподобного описания природы должна лежать симметрия. И если когда-нибудь появится настоящая теория Вселенной – в которой унифицированы все силы, а все компоненты подчиняются небольшому количеству правил, – нам потребуется вскрыть лежащую в основе симметрию, упрощающий принцип, на котором строится все остальное. В конце концов, поиски единой всеобъемлющей теории природы, по сути, сводятся к поиску симметрии Вселенной. Отдельные компоненты этой всеобъемлющей теории имеют свои собственные симметрии, такие как внутренняя симметрия калибровочных полей, которые дают нам лучшие современные описания электромагнитных, сильных и слабых взаимодействий… с точки зрения общей картины Платон во многом был на верном пути, определив некоторые из ключевых элементов головоломки, такие как симметрия, дуальность и общий принцип геометризации, которые, как мы сейчас полагаем, должны быть включены в любые реальные попытки объяснить картину мира».
Мы же не считаем, что в основе любого правдоподобного описания природы должна лежать симметрия. В своей глубинной основе Вселенная не симметрична, а иерархична. Частные симметрии отдельных ее компонентов не могут быть взаимодополняющими аспектами единой всеобъемлющей симметрии, так как относятся лишь к отдельно взятому уровню иерархии. Разные же уровни не связаны между собой симметрией, а более высокий уровень доминирует над более низким, так что события, не связанные между собой причинно-следственной связью на более низком уровне, могут быть связаны таковой на более высоком. Иерархичность Вселенной не отражена в достаточной степени в европейской идеалистической философии, зато хорошо отражена в восточной. Поэтому мы считаем надлежащий синтез платонизма с восточной философией более совершенной основой для теоретической физики, чем платонизм в чистом виде. Но такой подход принципиально ограничивает действие принципа геометризации в физике, как неподходящего для описания иерархичности. В отличие от математики, в информатике иерархичность играет немаловажную роль (например, 15-уровневая модель ЭМЗАС [3], 7-уровневая сетевая модель OSI, 3-уровневая архитектура ANSI/SPARC, иерархическая модель данных). Мы считаем, что идею Минковского о предустановленной гармонии между чистой математикой и физикой необходимо заменить идеей о предустановленной гармонии между чистой математикой, информатикой и физикой.
Рецензенты:
Белокуров С.В., д.т.н., доцент, начальник кафедры математики и естественнонаучных дисциплин, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж;
Душкин А.В., д.т.н., доцент, начальник кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж.
Работа поступила в редакцию 26.03.2014.