В учебной литературе [1–4 и др.] по тепломассообмену для студентов энергетического и электротехнического направления рассмотрены задачи стационарной теплопроводности, при решении которых приводится обоснование коэффициента теплопередачи, термического сопротивления стенки и эффективного коэффициента теплообмена. Представляет методический и практический интерес в обобщенной постановке нестационарной задачи теплопроводности с неравномерно распределенными внутренними источниками теплоты.
Постановка задачи
Пусть тепловыделяющая система состоит из произвольного числа тепловыделяющих, диэлектрических элементов (или наряду с ними каналов для прохождения охлаждающих сред или теплоносителей) с геометрическими размерами ξ1, ξ2, ξ3, ..., ξi+1, ξm+1. Коэффициенты теплопроводности материалов и сред являются известными и постоянными величинами. О переменности их свойств – от времени, координат, температуры, структуры конкретного материала будем учитывать через эффективные значения – λi. Внутри твэлов действуют внутренние источники теплоты – qVj(ξ, τ). Они являются функциями, по крайней мере, непрерывными, дифференцируемыми и интегрируемыми в пределах линейного размера элемента j (1, 2, 3, ..., i, ..., m). Имеют место ограниченные величины qVj(ξ, τ) ≤ Mj. Принимается, что температурное поле в тепловыделяющем элементе (твэле) и канале симметрично плоскости ξ = 0.
В диэлектрических слоях (или в охлаждающих каналах) внутренние источники теплоты зачастую принимаются равными нулю, но может иметь место при наличии химических реакций теплоперенос с фазовыми превращениями (кипение теплоносителя, конденсация паров, плавление, кристаллизация и т.п.). Заданы постоянные во времени коэффициенты теплообмена – α1, α2, т.е. теплообмен с внутренней и внешней поверхности тепловыделяющей системы осуществляется по закону Ньютона. Физически это означает, что температурное поле в системе твердых тел не зависит от закона распределения температур в средах – Tж1, Tж2. Существование изотермических поверхностей или отсутствие теплоты по другим направлениям (кроме ξ) говорит о его одномерном изменении. На границах контакта элементов существует идеальный контакт.
Система уравнений, описывающая нестационарный процесс теплопроводности в тепловыделяющей системе, имеет вид
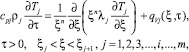(1)
где N – общее число элементов.
Начальные условия
Tj(ξ, τ = 0) = THj(ξ),
граничные условия
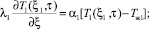
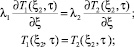
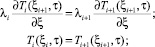
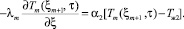
Здесь ξ – обобщенная координата; τ – текущее время; ξi – координата на границе соприкосновения слоев; n = 0, ξ = x – неограниченная пластина; n = 1, ξ = r – цилиндр; n = 2, ξ = r – шар; Tj(ξ, τ), Tж1, Tж2, qVj(ξ, τ) – соответственно температуры твэла, окружающих сред и функции тепловыделения; cpj, ρj, λj, λi – соответственно удельная массовая изобарная теплоемкость, плотность, коэффициенты теплопроводности конкретного элемента.
Проверка математической модели. Необходимость в проверке вызвана тем, что в литературе имеют место некорректно сформулированные математические модели.
Первый способ проверки. Будем исходить из физических размерностей всех величин. Пусть, например, n = 2 – шар, j = 1, 2. Дифференциальное уравнение теплопроводности в левой и правой части имеют размерность Вт/м3:
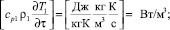
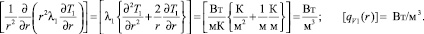
Таким образом, по размерности физических величин система уравнений записана верно.
Второй способ проверки. Число дифференциальных уравнений в частных производных – N после их решения будет в общем решении содержать 3N констант интегрирования. Докажем это. Пусть j = 1,2; N = 2, т.е. рассматриваются всего два элемента. Для этого случая необходимо задать 6 краевых условий. В этом можно легко убедиться.
Третий способ проверки. Для стационарного режима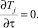 
Если внутренние источники теплоты – постоянные величины или равны нулю, то получим известные в литературе решения. Наличие переменного по координате источника теплоты приводит к сложному аналитическому решению [5], но для реализации на ЭВМ они не представляют трудностей.
Пример 1. В стационарном режиме в тепловыделяющей сборке (рисунок) с геометрическими размерами r0 = 0,02 м, r1 = 0,01 м, r2 = 0,0105 м, r3 = 0,029 м, r4 = 0,0295 м. Тепловыделение изменяется по зависимости:
qv = qv0∙(1 + b∙r2),
где
qv0 = 5,19∙105 Вт/м3,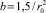 
;
r = 0,0275 м, α1 = 40000 Вт/(м2∙K);
α1 = 10 Вт/(м2∙K), Tж1 = 573,15 K;
Tж2 = 293,15K, λ1 = λ3 = 23 Вт/(м∙К);
λ2 = 15 Вт/(мК).
Найти максимальную температуру в тепловыделяющей сборке.
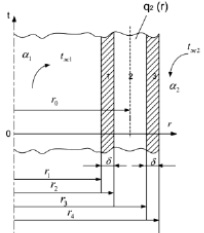
Схема задачи: 1,3 – оболочки; 2 – полый цилиндрический тепловыделяющий элемент
Решение. Определим термические сопротивления оболочек
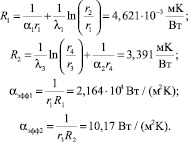
Введем безразмерные числа. Число Био
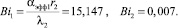
Функция Померанцева
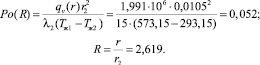
Окончательное решение задачи (1) для стационарного режима имеет вид
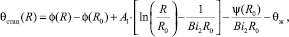(2)
где
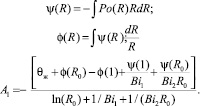
Для нашего примера, согласно (2),
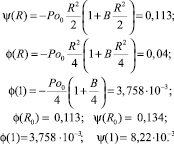
Тогда максимальная температура в тепловыделяющей сборке будет равна
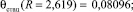
Tстац(r0 = 0,0275) =
= Tж1 + θстац(R = 2,619) (Tж1 – Tж2) = 322,7 °С.
Пример 2. Определите распределение температуры по радиусу в полом цилиндрическом тепловыделяющем элементе с оболочками, если принять постоянное по радиусу тепловыделение qV(r) = qV0. Какова максимальная погрешность расчета при такой замене тепловыделения в полом цилиндрическом твэле?
Решение:
Схема задачи приведена на рисунке. Окончательное решение задачи (1) для данного случая имеет вид
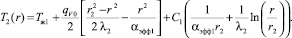
Здесь
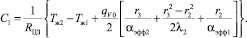(3)
Подставляя исходные данные qV0 = 5,19∙105 Вт/м3, находим значения C1 = 134,694 Вт/м, RЦЗ = 3,463 мК/Вт.
Погрешность расчета распределения температур по радиусу относительно точных температур
|
r, 10–3 м |
T2(r), K Расчет по (1) |
ε, % |
|
10,5 12,0 14,0 16,0 20,0 22,0 r0 = 23,0 26,0 29,0 |
573,617 574,524 575,458 576,138 576,897 577,026 577,036 576,865 576,418 |
0,254 0,761 1,328 1,797 2,503 2,758 3,07 3,08 3,15 |
Погрешность расчета в сравнении с расчетом по формуле (2)
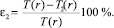
где T(r) – точное значение, К.
Координата максимальной температуры
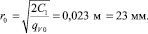
Как показывает анализ проведенного расчета максимальная погрешность распределения по радиусу температур не превышает 3,3 %, а по определению координаты максимальной температуры r0 ≈ 16,4 %
Вывод
Приведен пример расчета стационарного температурного поля в полом цилиндрическом тепловыделяющем элементе с оболочками. Показано, что погрешность расчета по сравнению с точным сложным решением не превышает 3,3 %.
Рецензенты:
Архипов В.А., д.ф.-м.н., профессор, заведующий отделом газовой динамики и физики взрыва НИИ прикладной математики и механики Томского государственного университета, г. Томск;
Борисов Б.В., д.ф.-м.н., доцент, профессор кафедры теоретической и промышленной теплотехники Томского политехнического университета, г. Томск.
Работа поступила в редакцию 18.03.2014.