Теория диагностики прочности адгезионных соединений композиционных материалов акустоэлектромагнитным методом (АЭМ), опираясь не только на аналитический базис учения о распространении акустических волн в композиционных материалах, но и учения об адгезии, теории прямого пьезоэлектрического эффекта, излучения и распространения электромагнитных волн, учения об когерентном кооперативном (КК) эффекте, дает аналитическое решение наблюдаемой связи электромагнитного излучения (ЭМИ) с адгезионной прочностью (АП). Модель композиционного материала можно представить, как правило, в виде многослойной конструкции, но использование ее резонансных свойств не дает ответа на наличие зависимости ЭМИ от адгезионной прочности реализованной в АЭМ [9]. И уж тем более эту зависимость нельзя объяснить математическими приемами по распознаванию образов [4].
Таким образом, задачей этой работы является описание с использованием термодинамического потенциала зависимости между прочностью адгезионного соединения и электромагнитным излучением когерентной кооперативной системы модифицирующих адгезив частиц кристаллитов сегнетокерамики (КС). Чтобы решить эту задачу, была предпринята попытка объяснить поведение модифицирующей частицы КС, являющейся частью КК ансамбля таких же частиц, ее термодинамическим потенциалом, так как эта частица находится в термодинамическом равновесии с окружающей ее средой сформированного адгезионного соединения.
Экспериментально было показано, что механические и электрические напряжения влияют на ЭМИ частицы КС [1]. Также было показано, что ЭМИ возникает за счет прямого пьезоэлектрического эффекта при сжатии и растяжении частиц упругой волной [10] при условии, что частица находится в КК системе подобных частиц. Кроме того было показано, что процесс полимеризации клеящего полимера не меньше влияет на величину ЭМИ [11]. Авторами работ [2, 3, 5–8] был сделан вывод, что механические напряжения, возникающие в процессе формирования адгезионного соединения за счет усадки или набухания адгезива, а также за счет формирования переходного (пограничного) слоя [11] определяют АП композиционных материалов и условия трансформации частицами упругих колебаний в ЭМИ [14]. Причем при модификации частицами КС остаточные напряжения не исчезают, а лишь перегруппировываются в адгезиве [16]. В то же время остаточные напряжения концентрируются на частицах и изменяют их термодинамический потенциал в пределах T < T0, а T0 – температура фазового перехода частицы КС второго рода. Термодинамический потенциал является обобщенной характеристикой макроскопического состояния частиц КК ансамбля и является отправной аксиомой АЭМ.
Частица, помещенная в адгезив, в котором создают упругие волны, описывается согласно Ландау [13] полным термодинамическим потенциалом W(T, σ, η, E)
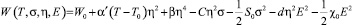(1)
где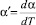 
– постоянный термодинамический коэффициент системы; η – внутренняя деформация кристаллита под действием постоянных и переменных напряжений; σ –действующие на кристаллит механические напряжения; E – напряженность электрического поля, в котором находится кристаллит (в нашем случае это поле отсутствует); β – термодинамическая постоянная (положительная величина); C – теплоемкость материала кристаллита; S0 – упругость материала кристаллита; d – пьезоэлектрический модуль материала кристаллита; χ0 – диэлектрическая восприимчивость материала кристаллита сегнетокерамики при неизменном значении внутренней деформации.
Рассматривая состояние частицы, полагаем, что она находится в равновесии с окружением, так как действие упругих волн лежит в области линейной зависимости величины деформации от механических напряжений. Это условие позволяет происходящий процесс характеризовать производной термодинамического потенциала по внутренней деформации при условии равенства производной нулю, т.е.
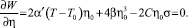(2)
Уравнение (2) имеет решение при T < T0 и описывает величину деформации усредненного диполя частицы под действием остаточных напряжений
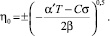(3)
В сегнетоэлектриках некоторые пьезоэлектрические модули, характеризующие изменение электрической поляризации под действием механических напряжений, достигают в области фазовых переходов весьма больших значений. Поэтому пьезоэлектрические модули определяют величину остаточной поляризации Pc элементарной ячейки под действием остаточных напряжений σ [12], которая может быть выражена в виде:
Pc = аη0, (4)
где a – заряд элементарной ячейки; η0 – внутренняя деформация в положении устойчивого равновесия. Используя решение (3), остаточная поляризация частицы примет вид
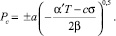(5)
Выражение (5) описывает зависимость остаточной поляризации от остаточных механических напряжений среды. Знаки «плюс» и «минус» отвечают двум возможным направлениям ориентации частицы.
Частица является элементом КК системы, у которой дипольные моменты частиц ориентированы вдоль оси – Z. Диэлектрические и другие свойства частицы в направлении осей X и Y при этом не обнаруживают никакой аномалии. Поэтому для исследования свойств вдоль оси Z достаточно рассмотреть в термодинамическом потенциале только члены, содержащие Pz. Это позволяет упростить рассмотрение задачи, избавляя ее от тензорного и векторного исчисления. Учитывая тот факт, что механические поля в частицах КС можно считать однородными.
Чтобы получить из адгезионной среды, модифицированной частицами КС, зависимость (5), содержащую информацию об остаточных напряжениях в адгезиве, влияющих на прочность клеевого соединения, изделие подвергают воздействию упругих колебаний, в такт которым сжимаются и растягиваются частицы КС, а значит, и усредненные дипольные моменты частиц, уменьшаются и увеличиваются. Колеблющиеся дипольные моменты частиц находящихся в КК системе, излучают электромагнитные волны, которые, интерферируя, усиливаются в точке их регистрации. Анализ зависимости амплитуды ЭМИ от остаточной ориентации усредненного диполя частицы позволяет получить информацию об остаточных механических напряжениях вокруг нее.
Рассматривая остаточную поляризацию частицы как диполь, колеблющийся под воздействием механической деформации (прямой пьезоэффект), получим составляющие электрической поляризации, связанные с деформацией частицы линейной зависимостью
Pi = dikXk, (6)
где Pi – составляющая вектора поляризации (i = 1,2,3); dik – пьезоэлектрическая постоянная, характеризуемая выражением (5), Xk – составляющая деформации по основным осям пьезокристалла (k = 1,…,6).
Выражение (6) с учетом выражения (5) и учетом того фактора, что Xk деформация по основным осям пьезокристалла имеет временной характер, даёт зависимость
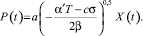(7)
Решая задачу излучения диполя на основании законов электродинамики [15], введем вектор Герца, в качестве которого примем отдельный диполь, дипольный момент которого характеризуется выражением (7), тогда
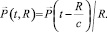(8)
Значение вектора Герца в момент времени t в точке, находящейся на расстоянии R, от осциллятора, определяется значением электрического момента осциллятора в момент времени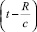 
, где c – скорость распространения ЭИ. Тогда выражение (8) удовлетворяет волновому уравнению
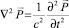(9)
Решение уравнения (9) позволяет найти напряженности электрического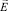 
и магнитного 
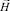поля ЭИ. Для этого предположим, что:
1. 
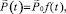(10)
где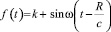 
– произвольная скалярная функция времени, k = 1, 2, 3,…
2. Решение ищем в сферической системе координат R, α, θ с центром в осцилляторе и с полярной осью, параллельной дипольному моменту –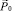 
частицы и оси Z КК системы.
3. Точка регистрации электромагнитного излучения находится в зоне, определяемой выражением (1/R) ⟩⟩ ω/c.
Решение (9) с учетом сделанных предположений будет иметь вид
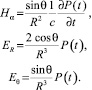(11)
А величина усредненного дипольного момента частицы с учетом выражения (10) может быть записана в виде
P(t) = aη0bsin ω0t = Pmsin ω0t, (12)
где aη0 – амплитуда изменения усредненного дипольного момента под действием упругих волн; ω0 – частота упругих колебаний; b – амплитуда ультразвуковых колебаний на диполе. Тогда. подставляя выражение (12) в (11), получим решение в виде
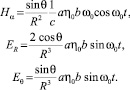(13)
Так как датчик в экспериментах регистрирует лишь азимутальную составляющую электрического поля, дальше будем анализировать третье уравнение из системы (13). Из-за ориентации датчика θ = 90° азимутальную составляющую электромагнитного поля запишем в виде
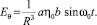(14)
Подставляя в выражение (14) величину внутренней деформации частицы КС, зависимую от остаточных напряжений (3), получим зависимость напряженности электрического поля от остаточных напряжений
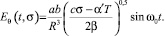(15)
Тогда зависимость остаточных напряжений от величины амплитуды ЭМИ будет иметь вид
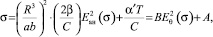(16)
где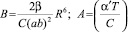 
, и представляют величины характеризующие свойства частицы КС; 
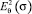– величина характеризует квадрат амплитуды ЭМИ. Выражение (16) не зависит от частоты упругих колебаний.
Подставим выражение (16) в уравнение Бикермана [3], предварительно модифицировав его.
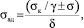(17)
где γ – коэффициент концентрации напряжений, обусловленный различием в механических свойствах адгезива с субстратом и δ – макроскопической неоднородностью субстрата; σ – остаточные напряжения в клеящем полимере; σк – когезионная (истинная) прочность заполимеризованного клеящего полимера. Уравнение (17) описывает прочность всех типов адгезионных соединений, модифицированных частицами, знак плюс для адгезива типа эластомер, знак минус для адгезива типа эпоксидная смола.
Подставляя в (17) выражение (16) получим зависимость, связывающую прочность модифицированного клеевого соединения с амплитудой ЭМИ, возникающей при стимуляции КК системы частиц КС акустическими колебаниями в виде
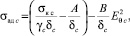(18)
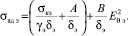(19)
Выражения (18) и (19) имеют параболический вид. В силу действительности значений σад и Eθ выражения (18) и (19) отображаются в первом квадранте декартовой системы координат. Ввиду того, что коэффициенты концентрации напряжений, обусловленный макроскопической неоднородностью склеиваемых субстратов, равны δс ≈ δэ, γс ≈ γэ, независимо от типа адгезива (c – эпоксидный адгезив, э – эластичный адгезив), а их когезионные прочности отличаются на порядок, то можно сделать следующие допущения.
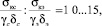
а
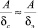
и
, 
, 
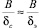
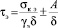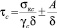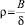
Это позволяет выражения (18) и (19) привести к виду
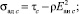(20)
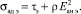(21)
Из справочных данных следует, что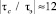 
. Поделив оба уравнения на τэ, получим
.
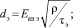
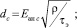
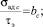
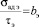Тогда результаты вычислений в относительных единицах будут иметь вид
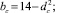(22)
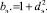(23)
Эти результаты можно представить на диаграмме (рисунок) в виде ветвей парабол в относительных единицах, которые описывают экспериментально полученные результаты [11] и совпадают с наблюдаемыми свойствами пьезоэлектрического модуля от всестороннего давления.
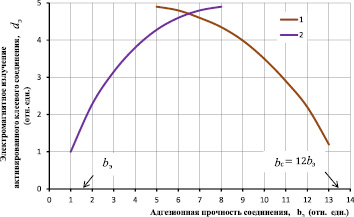
Теоретическая зависимость электромагнитного излучения адгезионного соединения модифицированного когерентной кооперативной системой частиц кристаллитов сегнетокерамики от адгезионной прочности: 1 – адгезив хрупкий (тип – отвержденная эпоксидная смола), 2 – адгезив эластичный (тип – каучукообразный адгезив). Ось абсцисс построена в относительных единицах адгезионной прочности соединения на основе эластомера – τэ, ось ординат построена в относительных единицах электромагнитного излучения адгезионного соединения на основе эластомера
Выводы
1. Разработана теоретическая модель зависимости электромагнитного излучения от адгезионной прочности. Отправной аксиомой для разработки модели явился термодинамический потенциал макроскопического состояния частицы кристаллита сегнетокерамики когерентной кооперативной системы. Представленная модель хорошо согласуется с экспериментальными результатами, которые опубликованы в работе [11] и отражены там же на рисунке.
2. Показано, что чувствительность метода зависит от свойств модифицирующих частиц. В качестве таких добавок рассмотрены частицы кристаллитов сегнетокерамики. Следовательно, подбирая материалы, можно варьировать чувствительность метода.
3. Полученная модель позволяет при создании регистрирующей аппаратуры учитывать свойства зависимости и уменьшать отношение сигнала к шуму, увеличивая полезный сигнал.
Рецензенты:
Капранов Б.И., д.т.н., профессор кафедры «Физические методы и приборы контроля качества», ФГБУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Плешанов В.С., д.т.н., доцент, ученый секретарь, ФГБУН «Институт физики прочности и материаловедения» Сибирского отделения Российской академии наук, г. Томск.
Работа поступила в редакцию 18.03.2014.