Рассмотрим класс обыкновенных дифференциальных уравнений следующего вида
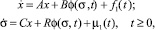 (1)
(1)
где A, B, C, R – постоянные матрицы порядков n×n, n×m, m×n, m×m соответственно, функция φ(σ, t) = (φ1(σ, t), ..., φm(σ, t)) является периодической по σ и непрерывной по совокупности аргументов (σ, t), f1(t), μ1(t) – заданные непрерывные вектор-функции размерностей n×1 и m×1 соответственно.
Определение. Говорят, что система (1) имеет периодическое решение, если существует число T > 0 такое, что x(t) = x(t + T), σ(t) = σ(t + T) для любого t ≥ 0. Такое периодическое решение часто называют предельным циклом первого рода.
Ставится следующая задача: найти необходимые и достаточные условия существования предельных циклов первого рода в системе (1).
Постановка задачи
Рассмотрим решение задачи для системы дифференциальных уравнений (1), когда φ(σ, t) является заданной периодической функцией по σ. Полагаем, что функция φ(σ, t) удовлетворяет условию Липшица по σ и непрерывна по совокупности аргументов (σ, t) ∈ Rm×I, I = [0, ∞). Функции f(t), μ(t) непрерывны по t, t ≥ 0. Введем обозначения:

где  ,
, 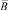 , P1, P2 – постоянные матрицы порядков (m + n)×(m + n), (m + n)×m, n×(n + m), m×(n + m), n×(n + m), m×(n + m), соответственно, In, Im – единичные матрицы порядков n×n, m×m соответственно.
, P1, P2 – постоянные матрицы порядков (m + n)×(m + n), (m + n)×m, n×(n + m), m×(n + m), n×(n + m), m×(n + m), соответственно, In, Im – единичные матрицы порядков n×n, m×m соответственно.
Теперь уравнение (1) запишется в виде
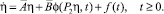 (2)
(2)
Предположим, что система (2) имеет периодическое решение η*(t) = η*(t + T*), ∀t ≥ 0, где T* – период. Тогда вдоль периодического решения выполняется равенство
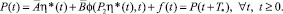
Пусть значение  . Тогда
. Тогда  Поскольку периодическое решение определяется значениями фазовых координат в пределах периода, то для построения периодического решения следует рассмотреть значения t ∈ I* = [0, T*].
Поскольку периодическое решение определяется значениями фазовых координат в пределах периода, то для построения периодического решения следует рассмотреть значения t ∈ I* = [0, T*].
Рассмотрим общий случай, когда имеются фазовые ограничения следующего вида
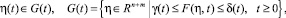 (3)
(3)
где 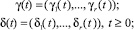 δ(t) = (δ1(t); ..., δr(t)), t ≥ 0 – заданные непрерывные функции, F(η, t) – непрерывная по совокупности аргументов (η, t) вектор-функция, F(η, t) = (F1(η, t), ..., Fr(η, t)).
δ(t) = (δ1(t); ..., δr(t)), t ≥ 0 – заданные непрерывные функции, F(η, t) – непрерывная по совокупности аргументов (η, t) вектор-функция, F(η, t) = (F1(η, t), ..., Fr(η, t)).
Ставится следующая задача: Найти необходимые и достаточные условия существования T* – периодического решения системы (2), (3).
Принцип погружения
Основой предлагаемого подхода к решению задачи является принцип погружения, который позволяет свести исходную задачу к задаче оптимального управления со свободными правыми концами траекторий.
Рассмотрим управляемую систему следующего вида
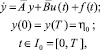 (4)
(4)
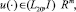 (5)
(5)
где η0 ∈ Rn+m – неизвестный вектор; T – неизвестный момент времени.
Введем следующие обозначения
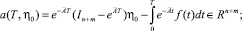 (6)
(6)
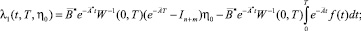 (7)
(7)
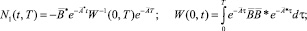 (8)
(8)
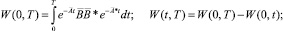 (9)
(9)
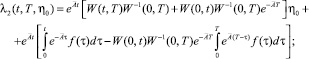 (10)
(10)
 (11)
(11)
Лемма 1. Если ранг матрицы

равен m + n, то матрица W(0, T) положительно определенна для любого T > 0.
Доказательство. Легко убедиться в том, что ранг блочной матрицы 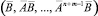 равен рангу матрицы Q. В самом деле, поскольку
равен рангу матрицы Q. В самом деле, поскольку

то 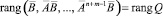
Если 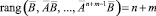 , то система алгебраических уравнений относительно z, определяемая выражением
, то система алгебраических уравнений относительно z, определяемая выражением
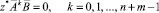 (12)
(12)
имеет единственное решение z = 0. Поскольку для любого t матрица
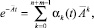
где функции αk(t), 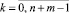 линейно независимы, то соотношение (12) равносильно следующему уравнению относительно z
линейно независимы, то соотношение (12) равносильно следующему уравнению относительно z
 (13)
(13)
которое также имеет единственное решение z = 0. Теперь рассмотрим квадратичную форму
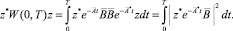
Так как z*W(0, T)z ≥ 0, ∀z, и она обращается в нуль тогда и только тогда, когда z = 0, то квадратичная форма z*W(0, T)z > 0 для любого z ∈ Rn+m, z ≠ 0. Следовательно, матрица W(0, T) > 0. Лемма доказана.
Теорема 1. Пусть rangQ = m + n. Тогда управление u(∙) ∈ L2(I, Rm) переводит траекторию системы (4), (5) из любого начального состояния y(T) = η0 ∈ Rn+m в состояние y(T) = η0 ∈ Rn+m тогда и только тогда, когда
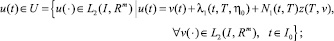 (14)
(14)
где функция z(t) = z(t, v(∙)), t ∈ I0 является решением дифференциального уравнения
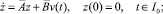 (15)
(15)
v(∙) ∈ L2(I, Rm). (16)
Решение дифференциального уравнения (4) при условии (5), соответствующее уравнению u(t) ∈ U, определяется по формуле
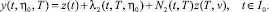 (17)
(17)
Доказательство. Решение дифференциального уравнения (4), исходящее из точки y(0) = η0, запишется так
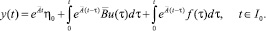 (18)
(18)
Отсюда при  имеем
имеем
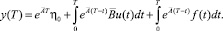
Тогда искомое управление u(t), для которого y(T) = η0, является решением следующего уравнения
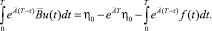 (19)
(19)
Так как матрица  неособая, то после умножения правой и левой части (19) на
неособая, то после умножения правой и левой части (19) на 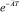 получим
получим
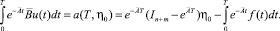 (20)
(20)
Множество всех управлений u(∙) ∈ L2(I, Rm), удовлетворяющих условию (20), обозначим через V, т. е.
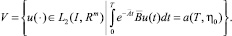 (21)
(21)
Заметим, что множество V содержит те и только те управления, которые переводят траекторию системы (4) из начального состояния y(0) = η0 в состояние y(T) = η0, где η0 ∈ Rn+m – любой вектор.
Теорема утверждает, управление u(t) принадлежит множеству (21) тогда и только тогда, когда оно является элементом множества U, т.е. что V = U.
Таким образом, общее решение интегрального уравнения (20) определяется соотношением (14).
Докажем, что V = U. Для этого достаточно показать, что: U ⊆ V и V ⊆ U. Покажем, что U ⊆ V. В самом деле, если u(t) ∈ U, то, как следует из соотношения (14), значение интеграла
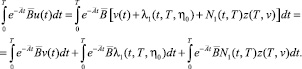 (22)
(22)
Так как (см. (15), (16))
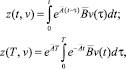
то  (23)
(23)
Интеграл (см. (7))
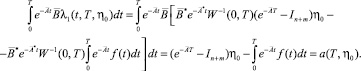 (24)
(24)
Последнее слагаемое из (22) с учетом соотношения (8) запишется в виде
 (25)
(25)
Теперь соотношение (25) с учетом выражений (26)–(28) запишется так
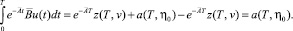 (26)
(26)
Из (26) следует, что управление u(t) ∈ U принадлежит множеству V. Итак, любое управление u(t) ∈ U является элементом множества V. Это означает, что множество U ⊆ V.
Покажем, что V ⊆ U. Пусть u*(t) ∈ V – любое управление из V, т.е.
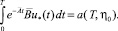 (27)
(27)
Рассмотрим соотношение (14), где v(∙) ∈ L2(I, Rm) – произвольная функция. Выберем v(t) = u*(t) ∈ L2(I, Rm). Тогда
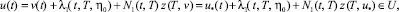 (28)
(28)
где функция z(t, u*), t ∈ I0 является решением дифференциального уравнения
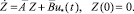 (29)
(29)
Решение дифференциального уравнения (29) имеет вид
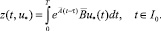
Отсюда при t = T с учетом (29) получим
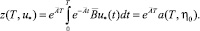 (30)
(30)
Как следует из формул (6)–(8), (30),

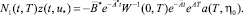
Теперь соотношение (28) запишется в виде
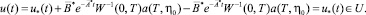
Таким образом, любая функция u*(t) ∈ V является элементом множества U. Следовательно, V ⊆ U. Из включений U ⊆ V, V ⊆ U следует, что U = V. Первое утверждение теоремы доказано.
Подставляя значение u(t) ∈ U из соотношения (14) в правую часть выражения (18) с учетом равенства W(0, T) = W(0, t) + W(t, T) получим представление решения системы (2) в виде (17). Теорема доказана.
Вдоль периодического решения системы (2) выполнено тождество P(t) = P(t + T*), t ≥ 0. Данное тождество запишется в виде
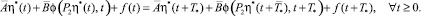
Отсюда, с учетом того, что η*(t) = η*(t + T*), t ≥ 0, имеем
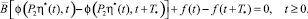
В частности, для значений t ∈ I* = [0, T*] данное тождество записывается в виде
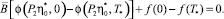
С учетом особенности периодических решений, исходная задача может быть записана в виде
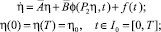 (31)
(31)
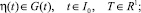 (32)
(32)
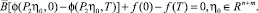 (33)
(33)
В дальнейшем будем рассматривать краевую задачу (31)–(33).
Лемма 2. Пусть rangQ = n + m. Тогда краевая задача (31)–(33) равносильна следующей задаче:
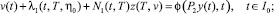 (34)
(34)
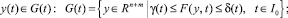 (35)
(35)
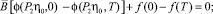 (36)
(36)
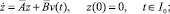 (37)
(37)
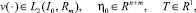 (38)
(38)
где функция y(t) = y(t; 0, η0), t ∈ I0 определяется по формуле (19).
Доказательство. Как следует из теоремы 1, для краевой задачи (4), (5) множество всех управлений, каждый элемент которого переводит траекторию системы из η0 в η0 за время T определяется по формуле (14). Сравнивая краевые задачи (4) и (30), можно убедиться в том, что управление u(t) ∈ U равно φ(P2y, t), t ∈ I0. При выполнении тождества (34) имеет место равенство η(t) = y(t), t ∈ I0. Следовательно, фазовое ограничение (3) запишется в виде (35). Для существования предельного цикла первого рода необходимо выполнение равенства (33). Теперь соотношение (33) запишется в виде (36). Из теоремы 1 следует, что функция y(t), t ∈ I0 имеет вид (17), где функция z(t), t ∈ I0 является решением дифференциального уравнения (37) при условии (38). Лемма доказана.
Рассмотрим следующую задачу оптимального управления: минимизировать функционал
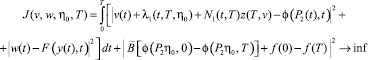 (39)
(39)
при условиях
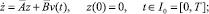 (40)
(40)
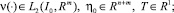 (41)
(41)
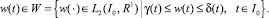 (42)
(42)
Вводя обозначения

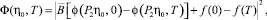
функционал (37) можно представить в виде
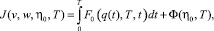
где функция y(t), t ∈ I0 определяется по формуле (17),

Обозначим через
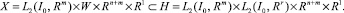
Допустимым управлением для задачи (39)–(42) является четверка ξ = (v, w, η0, T) ∈ X, а соответствующей этому управлению траекторией будет функция z(t) = z(t, v), t ∈ I0.
Следует отметить, что:
1) функционал J(ξ) = J(v, w, η0, T), ξ ∈ X ограничен снизу, так как J(ξ) ≥ 0 ∀ξ ∈ X;
2) задача (39)–(42) является задачей оптимального управления со свободными правыми концами траекторий с нестандартным функционалом;
3) в отличие от исходной задачи, уравнение движения системы является линейным.
Пусть
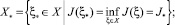

Теорема 2. Пусть rangQ = n + m, множество X* ≠ ∅. Для того, чтобы краевая задача (31)–(33) имела решение, необходимо и достаточно, чтобы значение J(ξ*) = J* = 0, где ξ* ∈ X – оптимальное управление для задачи (39)–(42). Если J* = J(ξ*) = 0, то функция
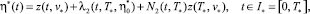 (43)
(43)
удовлетворяющая условию P(t) = P(t + T*), ∀t ≥ 0, является периодическим решением системы (2), (3).
Доказательство. Заметим, что значение функционала J* = J(ξ*) = 0 тогда и только тогда, когда выполнены тождества
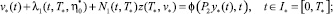
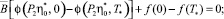
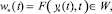
где
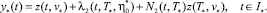
Из включения F(y*(t), t) ∈ W следует, что
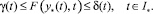
Таким образом, при J(ξ*) = 0 выполнены соотношения (34)–(38). Более того, найдено решение системы (34)–(38) v = v*(t),  T = T*, z(t) = z(t, v*), t ∈ I. Согласно утверждениям леммы 2, уравнения (34)–(38) равносильны краевой задаче (31)–(33). Следовательно, краевая задача (31)–(33) имеет решение. Верно и обратное утверждение, т.е. если краевая задача (31)–(33) имеет решение, то значение J(ξ*) = 0. Более того, решение краевой задачи (31)–(33), функция η*(t) = y*(t) t ∈ I*, t ∈ I*.
T = T*, z(t) = z(t, v*), t ∈ I. Согласно утверждениям леммы 2, уравнения (34)–(38) равносильны краевой задаче (31)–(33). Следовательно, краевая задача (31)–(33) имеет решение. Верно и обратное утверждение, т.е. если краевая задача (31)–(33) имеет решение, то значение J(ξ*) = 0. Более того, решение краевой задачи (31)–(33), функция η*(t) = y*(t) t ∈ I*, t ∈ I*.
Заметим, что функция η*(t) = y*(t) t ∈ I*, t ∈ I* будет периодическим решением системы (2), (4), если
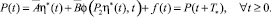
Теорема доказана.
Заметим, что:
1) если 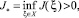 то независимо от того, пусто или не пусто множество X*, краевая задача (31)–(33) не имеет решения. Следовательно, исходная система (2), (4) не имеет периодического решения;
то независимо от того, пусто или не пусто множество X*, краевая задача (31)–(33) не имеет решения. Следовательно, исходная система (2), (4) не имеет периодического решения;
2) осуществлен последовательный переход от исходной задачи для системы (2), (3) к краевой задаче (31)–(33) и от нее к системе (34)–(38);
3) система (34)–(38) равносильна задаче оптимального уравнения (39)–(42).
Рецензенты:
Мухамбетжанов С.Т., д.ф.-м.н., профессор, зав. кафедрой «Дифференциальные уравнения и теория управления», Казахский национальный университет имени аль-Фараби, г. Алматы;
Калимолдаев М.Н., д.ф.-м.н., профессор, директор, Институт проблем информатики и управления Республики Казахстан, г. Алматы;
Бичурин М.И., д.ф.-м.н., профессор, заведующий кафедрой ПТРА, Новгородский государственный университет, г. Нижний Новгород.
Работа поступила в редакцию 18.03.2014.



