Операции забивки и извлечения свайных элементов занимают важное место в строительстве. Существует несколько способов погружения свай: ударный, вибрационный, статический, завинчиванием. Требования к темпам и качеству производства свайных работ диктуются не только проектными нормами, но и экономическими, экологическими и социальными аспектами.
В конструкцию современных вибропогружателей включают вибровозбудительную коробку с двумя, четырьмя или шестью вибрационными валами, захватывающий элемент, пригруз, амортизаторы.
Вибрационные валы при вращении посредством дебалансов создают циклическую вынуждающую силу. Составляющая вынуждающей силы, направленная вниз, носит название – погружающая, вдавливающая (Fв), а направленная вверх – подъёмная (Fп).
Большинство вибропогружателей выпускаются с симметричной вынуждающей силой. Применение симметричной Fп = Fв вынуждающей силы ведёт к использованию пригруза. Пригруз частично или полностью компенсирует подъёмную силу и обеспечивает погружение сваи.
Одним из направлений совершенствования вибропогружателя является применение асимметричной вынуждающей силы. В этом случае происходит изменение соотношения подъемной и вдавливающей силы, т.е. Fп < Fв. Применение асимметричной вынуждающей силы может повысить эффективность работы вибропогружателя при снижении металлоемкости.
Можно заключить, что влияние характера вынуждающей силы на эффективность погружения свайных элементов в настоящее время не может считаться до конца изученным вопросом.
Отношение значения вдавливающей силы Fв к подъёмной Fп носит название: коэффициент асимметрии. Коэффициент асимметрии может изменяться в широком диапазоне.
В соответствии с основными направлениями развития машин для свайных работ [5] в настоящей статье рассматривается одно из перспективных направлений развития способа вибропогружения свай и устройства для его осуществления.
Ранее выполненные работы [2, 3, 4, 6, 8, 9] позволяют продолжить исследования по повышению эффективности работы вибропогружателей.
Задачей исследований является создание средств вибровозбуждения, позволяющих получать высокий коэффициент силовой асимметрии при меньшем количестве элементарных вибровозбудителей за счёт улучшения закона изменения результирующей вынуждающей силы.
Существуют технические решения [7], содержащие универсальное вдавливающее устройство. Этот дебалансный вибровозбудитель направленного действия позволяет обеспечить в плавном (безударном) режиме погружение свай в грунт при семикратной асимметрии вынуждающей силы.
Недостатком такого и аналогичного [11] технического решения является невозможность получения высоких значений коэффициента асимметрии вынуждающей силы при уменьшении количества элементарных вибровозбудителей направленного действия.
В данной работе рассматривается способ получения асимметричных механических колебаний направленного действия.
Способ включает получение результирующей асимметричной вертикальной вынуждающей силы, составляющие которой генерируют с помощью n элементарных вибровозбудителей направленного действия.
Кратность отношений угловых скоростей вращения валов элементарных вибровозбудителей к угловой скорости первого вала соответствует числам натурального ряда от 1 до n.
Статический момент элементарных вибровозбудителей уменьшается с увеличением угловой скорости ωi.
Режим генерирования составляющих Fi возбуждающей силы F осуществляют по закону её изменения, определяемой зависимостью
F = F(t) = A cos2p ωt/2, (1)
разложение которой в ряд Фурье содержит гармоники (p – k) порядка
F(p-k) = А·[22p–1]–1 (2p)! [k!·(2p – k)!]–1 cos (p – k)·ω(p-k)t, (2)
где k = 0, 1, 2, …, (p – 1); 2p – порядок зависимости F(t); p – порядок наивысшей гармоники; A – амплитуда изменения вынуждающей силы.
Зависимость (2) получена следующим образом.
Элементарные вибровозбудители 2i представляют собой двухдебалансные вибраторы, создающие направленные силы инерции, изменяемые по гармоничному закону, представляют (с учётом кинематической связи их валов с передаточными отношениями зубчатых колёс в виде ряда натуральных чисел) гармоники ряда Фурье.
Для четной функции f(x) ряд Фурье [1] имеет вид
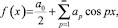 (3)
(3)
где коэффициенты Фурье
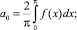 (4)
(4)
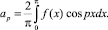 (5)
(5)
Из зависимости (3) получаем
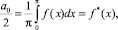 (6)
(6)
где f*(x) – среднее арифметическое функции f(x) на отрезке [0, π].
В качестве базовой функции для представления закона изменения вынуждающей силы для дебалансного вибровозбудителя направленного действия мультипликационного типа можно принять на интервале – π ≤ x ≤ π функцию
f(x) = A cos2p x/2, (7)
для которой среднее арифметическое значение
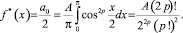 (6a)
(6a)
и которая может быть представлена конечным рядом из переменных членов (от k = 0 до k = p– 1) в виде
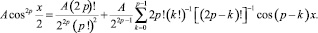 (8)
(8)
С учётом физической сущности процесса переменную x можно представить как ωt, где ω – угловая скорость (угловая частота) вращения вала, t – время в пределах периода T, при этом в зависимости (8) меняется вид последнего сомножителя (x заменяется на ωt, а в гармониках Ai cosiωt ряда Фурье Ai соответствуют силе Fi, генерируемой i-м вибровозбудителем.
Второе слагаемое зависимости (8) представляет сумму гармоник и после замены x на ωt каждая из них может быть представлена зависимостью (2).
С помощью зависимости (8) можно количественно оценить эффективность вибровозбуждения. Принимаем количество элементарных вибровозбудителей n = p = 7.
После преобразования и подстановки p = 7 во второе слагаемое зависимость (8) для вынуждающей силы F(7) имеем
F(7) = Acos2p − Aa0/2 = A [1/8192 (3003 cos x + 2002 cos 2x + + 1001 cos 3x + 364 cos 4x + + 91 cos 5x + 14 cos 6x + cos 7x]. (8а)
По зависимости (8а) получаем следующие соотношения, пропорциональные генерируемыми i-ми вибровозбудителями силам Fi:
А1/A = 3003/8192, А2/A = 2002/8192, А3/A = 1001/8192, А4/A = 364/8192,
А5/A = 91/8192, А6/A = 14/8192, А7/A = 1/8192. (8б)
Так как шестым и седьмым соотношениями амплитуд из ряда (8б) из-за незначительного их размера можно пренебречь, то практически достигается тот же силовой эффект и при пяти вибровозбудителях при законе изменения вынуждающей силы F = cos2px/2.
Из зависимости (2) c учётом конечности ряда при x = 0 имеем
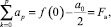 (9)
(9)
а при x = π/2
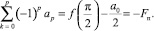 (10)
(10)
Параметры Fв и Fп обеспечивают оценку точности приближения ряда Фурье к функции f (x) при конечном числе членов ряда, меньшем p.
Для монотонно убывающей функции f(x) вибрационная система может быть оценена коэффициентом динамичности
kд = │Fв/Fп│ = [f(0) – f*(x)]/f*(x) = kа, (11)
т.е. коэффициенты динамичности системы и асимметрии вынуждающей силы совпадают, а параметры Fв и Fп являются соответственно модулями вдавливающей и подъёмной вынуждающей силы F.
Амплитуда или общая сила
A = │Aв│ + │Aп│, (12)
где Ав и Ап – амплитуды вдавливающей силы и подъёмной силы соответственно.
Подъёмная сила
Fп = Gв + Gс – Ап, (13)
где Gв и Gс – вес вибровозбудителя и вес сваи (естественный пригруз) соответственно, а их сумма является статической нагрузкой.
Получение заранее заданной вдавливающей силы Fв решается посредством числа гармоник при соответствующем подборе статических моментов. При увеличении числа элементарных вибровозбудителей сокращается время действия вдавливающей силы Fв на погружаемый элемент (сваю). Из закона сохранения количества движения следует, что чем меньше время воздействия Fв, тем больше время действия подъёмной силы Fп, тем меньше значение подъёмной силы Fп, т.е. уменьшение времени воздействия Fв позволяет получить меньшую подъёмную силу Fп.
Задавшись коэффициентом динамичности (силовой асимметрии) kд = kа = 8 с учётом статической нагрузки (Gв + Gc = Fп), строим два графика вынуждающей силы F(7) и F(5) (соответственно при 7 и 5 элементарных вибровозбудителях) за период T оборота вала первого вибровозбудителя (от 0 до 2π) со сдвигом по оси ординат на размер статической нагрузки (рисунок). Также наносим график вынуждающей силы F^ прототипа (при 7 элементарных вибровозбудителях и kд = kа = 7).
Из графика изменения вынуждающей силы предлагаемого вибровозбудителя видно, что при большем коэффициенте динамичности (силовой асимметрии) и равном или меньшем количестве элементарных вибровозбудителей в сравнении с прототипом функция более гладкая (без колебаний).
Вывод
Теоретические и аналитические исследования полигармонических вибровозбудителей направленного действия показывают, что технически возможно получение необходимых по асимметрии вынуждающих сил при наименьшем количестве элементарных вибровозбудителей.
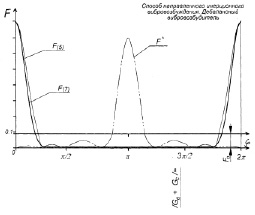
Изменение вынуждающей силы предлагаемого вибропогружателя с пятью и с семью элементарными вибровозбудителями аналога с семью элементарными вибровозбудителями
Рецензенты:
Богданов В.С., д.т.н., профессор, заведующий кафедрой «Механическое оборудование», Белгородский государственный технологический университет им. В.Г. Шухова, г. Белгород;
Севостьянов В.С., д.т.н., профессор, заведующий кафедрой «Технологические комплексы, машины и механизмы», Белгородский государственный технологический университет им. В.Г. Шухова, г. Белгород.
Работа поступила в редакцию 18.03.2014.



