Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Сетевые и графовые модели охватывают довольно широкий класс задач, встречающихся при проектировании систем, планировании работ, распределении продукции, организации транспортных перевозок, размещении различных центров обслуживания и т.п.

Задач, в которых используется понятие достижимости, довольно много. Вот одна из них. Граф может быть моделью какой-то организации или социальной сети, в которой люди представлены вершинами, а дуги интерпретируют каналы связи. При рассмотрении такой модели можно поставить вопрос, может ли информация от одного лица хi быть передана другому лицу хj, т.е. существует ли путь, идущий от вершины хi к вершине хj. Если такой путь существует, то говорят, что вершина хj достижима из вершины хi. Можно интересоваться достижимостью вершины хj из вершины хi только на таких путях, длины которых не превосходят заданной величины или длина которых меньше наибольшего числа вершин в графе и т.п. задачи.

Характерной особенностью таких задач является большая размерность, что обусловливает необходимость конструирования более скоростных алгоритмов. Плодотворной основой для построения таких алгоритмов могут служить их сетевые и графовые формализации [1, 7].

Программные реализации указанных задач весьма универсальны и просто программируемы при небольших размерностях графа. Однако при значительном увеличении количества узлов или дуг графа время программного решения при последовательном исполнении инструкций становится практически неприемлемым. Аппаратные реализации хотя и обеспечивают необходимую скорость за счет параллельной обработки информации, но не обладают достаточной алгоритмической гибкостью, в силу этого – их адаптация к изменениям логики вычислений не всегда возможна [2, 3, 4, 5]. Решением данной проблемы является использование таких вычислительных алгоритмов, которые бы совмещали скорость аппаратных вычислений с легкостью программной модификации в параллельных алгоритмах [6, 8, 9].

В рассматриваемых алгоритмах графы заданы с помощью матрицы смежности, которая дает его компактное представление, особенно если есть возможность работать с двоичными битами в машинном слове. Анализ алгоритмов решения оптимизационных задач на графах приводит к выводу, что большинство операций на графах могут выполняться параллельно для каждой из вершин, что позволяет значительно ускорить обработку данных.

Допустим, что мы имеем граф, структура которого описана матрицей смежности (рис. 1) размерностью n×n, (где n – число вершин графа), однозначно представляющая его структуру:

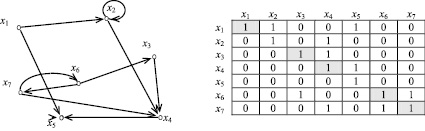
а б

Рис. 1. Пример 1: а ‒ граф; б ‒ матрица смежности графа

A = {aij}, i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

aij = 1, если существует дуга из вершины xi в вершину xj,

aij = 0, если нет дуги из вершины xi в вершину xj.

Достижимость в графе описывается матрицей достижимости

R = [rij], i, j = 1, 2, ... n, где n – число вершин графа, а каждый элемент определяется следующим образом:

rij = 1, если вершина хj достижима из хi,

rij = 0, в противном случае.

Множество вершин R(xi) графа G, достижимых из заданной вершины xi, состоит из таких элементов xj, для которых (i, j)-й элемент в матрице достижимостей равен 1. Очевидно, что все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из себя самой путeм длины 0. Поскольку прямое отображение 1-го порядка Г+1 (xi) является множеством таких вершин xj, которые достижимы из xi с использованием путей длины 1, то множество Г+(Г+1(xi)) = Г+2 (xi) состоит из вершин, достижимых из xi с использованием путей длины 2. Аналогично Г+p(xi) является множеством вершин, которые достижимы из xi с помощью путей длины p.

Так как любая вершина графа, которая достижима из xi, должна быть достижима с использованием пути (или путей) длины 0 или 1, или 2, ..., или p, то множество вершин, достижимых для вершины xi, можно представить в виде

R(xi) = {xi } ∪ Г+1 (xi) ∪ Г+2(xi) ∪ ... ∪ Г+p(xi).

Как видим, множество достижимых вершин R(xi) представляет собой прямое транзитивное замыкание вершины xi, т.е. R(xi) = T+(xi). Следовательно, для построения матрицы достижимости находим достижимые множества R(xi) для всех вершин xi ∈ X. Полагая rij = 1, если xj ∈ R(xi) и rij = 0 в противном случае.

Суть предлагаемого параллельного алгоритма нахождения матрицы достижимости заключается в следующем:

1. Так как каждая вершина достижима сама для себя, то в матрице достижимости R1 на главной диагонали должны стоять 1. Единицы можно предварительно занести на главную диагональ матрицы смежности, для того чтобы в п. 2 алгоритма использовать общую формулу преобразования.

2. По матрице смежности для каждой вершины графа xi находим строку в матрице R1 как результат логического сложения тех (j-х) строк матрицы смежности, для которых xij = 1

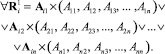
Например, для вершины x1 в матрице смежности элементы a11, a12 и a15 равны 1, следовательно, строка в матрице R1 для вершины x1 будет получена как результат логического сложения элементов соответствующих позиций первой, второй и пятой строк матрицы смежности.

Операция построения матрицы достижимостей R1 может быть выполнена параллельно для всех вершин графа.

3. По матрице R1 для каждой вершины графа находим матрицу следующего уровня R2 по аналогичным формулам:

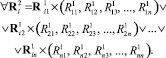
4. Далее процедура построения матрицы достижимости Rk по матрице достижимости предыдущего уровня Rk–1 повторяется до тех пор, пока Rk не будет равной Rk–1.

В нашем примере на рис. 1 построение матрицы достижимости произошло за одну итерацию, так как R2 = R1.

Количество итераций зависит от структуры графа, а именно от длины простых цепей и контуров. Рассмотрим второй пример, показанный на рис. 2. Как видим из примера, матрица достижимости строится за три итерации, то есть только R4 = R3. Таким образом, количество итераций равно длине самой длинной простой цепи и не зависит от количества вершин графа. В реальных сетевых моделях, где велика степень связности графа, скорость построения матрицы еще более возрастет.

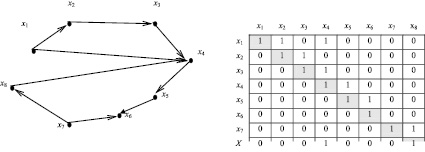
а б

Рис. 2. Пример 2: а ‒ граф; б ‒ матрица смежности графа

По сравнению с последовательным алгоритмом, в котором время выполнения зависит от размерности графа, предлагаемое решение позволяет значительно увеличить быстродействие.

Операция построения матрицы достижимости является ключевой в задаче разбиения графа на максимальные сильно связные подграфы, в задаче построения кратчайших путей и в ряде других задач.

Шатров А.В., д.ф.-м.н., профессор, зав. кафедрой «Математическое моделирование в экономике» Вятского государственного университета, г. Киров;

Бутаев М.М., д.т.н., профессор, ученый секретарь ОАО «НПП Рубин», г. Пенза.

Работа поступила в редакцию 26.02.2014.