Сложность протекания большинства технологических, а также природных процессов приводит к необходимости решения многокомпонентных задач и установлению многопараметрических зависимостей, что затрудняет построение точной математической модели.
установление аналитической многофакторной зависимости, которая может быть выявлена с помощью экспериментальных данных, является основным методом описания процесса. Но чем больше параметров исследования, тем более трудоемкими становятся вычисления, вследствие этого аналитические зависимости теряют свою наглядность.
Известно, что к наглядным методам относится геометрическое моделирование. Данный метод позволяет успешно прогнозировать динамику состояний различных компонентов природной среды. Наиболее эффективным представляется изучение процессов динамических систем и протекающих в них процессов, а также решение многих технических и управленческих задач путем нахождения неизвестной функции, описывающей рассматриваемый процесс, при условии, что известны соотношения, связывающие эту функцию и ее производные (дифференциальное уравнение) на их геометрических моделях.
Среди последних чаще всего используются статистические, аппроксимационные модели. Они строятся на основе данных, полученных в активном либо пассивном эксперименте. Аналитические зависимости, моделирующие процесс, трудно отнести к наглядным представлениям процесса. Замена же аналитических моделей на их геометрические аналоги значительно упрощает решение многих задач.
Геометрическое пространство и его элементы – это база, на которую опираются всевозможные методы геометрического моделирования. Возможность геометрического решения и геометрического описания многофакторной задачи приводит к конструкции, расположенной в многомерном пространстве. Как следствие, возникает задача однозначного взаимного отображения многопараметрических многомерных объектов на некоторые геометрические многообразия [5].
Анализ специальной литературы показал, что наибольшее распространение получили алгебраические и дробно-алгебраические поверхности, описываемые полиноминальными или дробно-полиноминальными зависимостями.
Цель исследования: применение метода геометрического моделирования для оценки качества атмосферного воздуха, установление зависимости изменения индекса загрязнения атмосферы (ИЗА) от метеорологических параметров комплексного и по отдельным загрязняющим веществам для прогнозирования возникновения той или иной экологической ситуации.
Разработка модели для оценки качества атмосферного воздуха начинается с выявления интервалов со значительным превышением уровня загрязнения атмосферы. Затем устанавливаются корреляционные зависимости между отмечавшимся в эти периоды увеличением предельно допустимых концентраций загрязняющих веществ (ПДК) и некоторыми метеорологическими параметрами, а также их определенными сочетаниями, рассматриваемыми в качестве предикторов. С учетом всех полученных данных разрабатывается модель прогноза качества атмосферного воздуха мегаполиса.
Выбор предиктантов обычно осуществляется из общих представлений о возможных причинах изменений концентраций примесей – изменении направления или скорости ветра, способности приземного слоя атмосферы города к самоочищению, вымывании или трансформации примесей. При этом используются некоторые качественные выводы теории атмосферной диффузии, в том числе о влиянии задерживающих слоев в приграничном слое атмосферы как причины изменения концентрации примесей.
Для получения зависимости динамики ПДК пяти основных загрязняющих веществ (сероводорода, диоксида серы, диоксида азота, оксида углерода, пыли) в атмосферном воздухе урбанизированной территории в зависимости от времени года, количества выпавших осадков, влажности воздуха, направления и скорости ветра использовались статистические данные, приведенные в табл. 1 и 2.
Таблица 1
Динамика средних показателей загрязняющих веществ г. Оренбурга относительно превышения ПДК в холодный период
|
№ п/п |
Температура воздуха Т, °С |
Осадки, мм |
Влажность, % |
Румб, d/10 |
Скорость ветра V, м/c |
Концентрации основных ЗВ, приведенных к ПДК |
||||
|
H2S |
NO2 |
SO2 |
Пыль |
CO |
||||||
|
1 |
–4,2 |
9,6 |
87 |
18 |
3,5 |
0 |
0 |
0 |
0 |
0 |
|
2 |
–14 |
0,5 |
77 |
20 |
5,3 |
0,001 |
0,01 |
0,001 |
0,1 |
1 |
|
3 |
–3,9 |
2,4 |
88 |
20 |
5 |
0,002 |
0,02 |
0,004 |
0,15 |
1,5 |
|
4 |
–11,4 |
0,7 |
81 |
20 |
4,3 |
0,003 |
0,03 |
0,005 |
0,2 |
2 |
|
5 |
–4,1 |
1,9 |
87 |
21 |
2,7 |
0,004 |
0,04 |
0,006 |
0,15 |
3 |
|
6 |
–8,5 |
0.4 |
81 |
27 |
4 |
0,005 |
0,05 |
0,008 |
0,1 |
4 |
|
7 |
–18,6 |
0,2 |
81 |
20 |
1 |
0,006 |
0,06 |
0,009 |
0,1 |
1,5 |
|
8 |
–8 |
0,9 |
82 |
16 |
3,6 |
0,008 |
0,08 |
0,01 |
0,2 |
2 |
|
9 |
–11,6 |
0,1 |
83 |
21 |
3,7 |
0,009 |
0,09 |
0,011 |
0,1 |
2 |
|
10 |
–15,3 |
0,4 |
96 |
15 |
2 |
0,01 |
0,1 |
0,013 |
0,1 |
3 |
|
11 |
–2,3 |
0,9 |
80 |
19 |
6 |
0,011 |
0,11 |
0,017 |
0,1 |
4 |
|
12 |
–14,5 |
0 |
93 |
22 |
2 |
0,013 |
0,12 |
0,02 |
0,15 |
0 |
|
13 |
1,2 |
0 |
85 |
10 |
5 |
0,08 |
0,13 |
0,03 |
0,2 |
1 |
Исследование поведения изменения ПДК позволило составить базу данных для построения универсальной математической модели прогнозирования качества атмосферы промышленного города.
метод геометрического моделирования позволяет учесть все факторы и параметры, необходимые для оценки качества атмосферного воздуха, и построить зависимость изменения ИЗА от метеоусловий как комплексного, так и по отдельным загрязняющим веществам. Выявленные закономерности изменения ИЗА от метеорологических параметров позволяют достаточно быстро оценить состояние экологического благополучия территории населенного пункта по качеству атмосферы. Причем погрешность данного метода лежит в пределах 15 % от наблюдаемой.
Для построения номограмм динамики комплексного ИЗА был использован метод группового учета аргументов. Данный метод позволяет использовать некоторое математическое обобщение метода графической регрессии, в котором субъективное построение кривых заменено построением зависимостей по способу наименьших квадратов. В данном методе аппроксимация нелинейной зависимости предиктанта ИЗА от предикторов xl, х2, х3, ..., xn (метеорологические условия) осуществляется за счет введения промежуточных переменных, определяемых парами предикторов [4].
Таблица 2
Динамика средних показателей загрязняющих веществ г. Оренбурга относительно превышения ПДК в теплый период
|
№ п/п |
Температура воздуха Т, °С |
Осадки, мм |
Влажность, % |
Румб, d/10 |
Скорость ветра V, м/c |
Концентрации основных ЗВ, приведенных к ПДК |
||||
|
H2S |
NO2 |
SO2 |
Пыль |
CO |
||||||
|
1 |
18,9 |
0,4 |
60 |
20 |
4,6 |
0 |
0 |
0 |
0 |
0 |
|
2 |
18,7 |
0,9 |
58 |
19 |
2,8 |
0,001 |
0,01 |
0,001 |
0,1 |
1 |
|
3 |
24 |
0,2 |
56 |
12 |
1,7 |
0,002 |
0,02 |
0,002 |
0,2 |
2 |
|
4 |
22,4 |
0,7 |
50 |
8 |
2,8 |
0,003 |
0,03 |
0,003 |
0,25 |
3 |
|
5 |
16,5 |
0,3 |
56 |
20 |
4,5 |
0,004 |
0,05 |
0,005 |
0,25 |
4 |
|
6 |
26,2 |
2,7 |
54 |
20 |
2,6 |
0,005 |
0,08 |
0,008 |
0 |
6 |
|
7 |
19,2 |
0,2 |
55 |
18 |
2,3 |
0,006 |
0,09 |
0,01 |
0,1 |
0 |
|
8 |
16,7 |
0 |
75 |
35 |
2 |
0,007 |
0,1 |
0,018 |
0,1 |
0 |
|
9 |
19,3 |
1,4 |
61 |
22 |
4,6 |
0,008 |
0,11 |
0,02 |
0,2 |
0 |
|
10 |
24,5 |
0,3 |
54 |
20 |
4,4 |
0,009 |
0,12 |
0,03 |
0 |
1 |
|
11 |
19,2 |
0 |
51 |
19 |
2 |
0,01 |
0,15 |
0,04 |
0,1 |
2 |
|
12 |
21,9 |
0 |
61 |
5 |
1,7 |
0,011 |
0,17 |
0,05 |
0 |
3 |
|
13 |
21,1 |
5,1 |
66 |
31 |
1 |
0,013 |
0,19 |
0,06 |
0,1 |
4 |
В качестве примера использования поверхностей плоскопараллельного переноса нами предложена модель зависимости изменения Индекса загрязнения атмосферы (ИЗА) в условиях тумана.
Если допустить, что факторы, определяющие гиперповерхность D (ИЗА), взаимно независимы, можно представить ее результат изменения параметров влажности, ветровой нагрузки, времени и температурного режима.
В этом случае уравнение такой поверхности будет иметь вид:
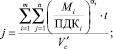(1)
где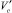 
– объем атмосферного воздуха, в котором рассеиваются примеси, м3; Mi – количество выбросов i-й примеси в атмосферу, т/год; m – число источников выбросов на территории населенного пункта; n – количество загрязняющих веществ; αi – безразмерная константа, позволяющая соотнести степень вредности i-го вещества с вредностью диоксида серы [3].
Наличие уравнения позволяет решать задачи на оптимальность.
Кроме того, при наличии достоверной информации, при необходимости, на данную систему могут быть наложены граничные условия, в свою очередь это позволит значительно повысить достоверность полученной модели.
При таком подходе факторно-параметрическое пространство изучаемого процесса, как правило, представляется расширенным евклидовым n-мерным пространством Еn+, где n – сумма числа факторов и параметров системы, а сам процесс и его компоненты рассматриваются как k-поверхности (k = 0, …, n – 1) этого пространства Еn+.
Вместе с этим следует отметить, что вид зависимости по таблицам исходных данных определить не представляется возможным, и полученные по экспериментальным данным статистические модели далеки от совершенства.
Однако анализ одномерных k-поверхностей (линий каркаса), принадлежащих конструируемой поверхности, во многих случаях позволяет определить вид искомой зависимости.
В пространстве аналитическая геометрия изучает поверхности, которые в прямоугольных декартовых координатах определяются алгебраическими уравнениями первой, второй и последующих степеней относительно Х, Y, Z:
Ax + By + Cz + D = 0; (2)
Ах2 + Ву2 + Сz2 + 2Dху + 2Ехz + 2Fуz + 2Мх + 2Nу + 2Lz + К = 0; (3)
Такой подход к построению геометрических моделей проходящих процессов позволяет значительно расширить базу исследуемых зависимостей, используемых для их описания.
регрессионные модели для ИЗА и связанных с ними концентраций основных загрязняющих веществ были созданы для определения количественных обусловленностей между параметрами. метеорологические показатели в данной системе обозначены как параметры-аргументы.
Применение полученного алгоритма с использованием статистических данных позволило построить номограммы динамики комплексного ИЗА для г. Оренбурга в условиях тумана, графические изображения которых представлены на рисунке [4].
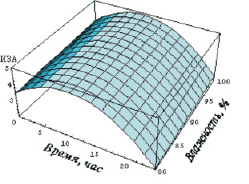
а
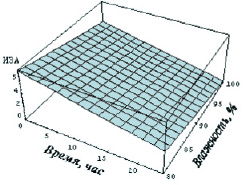
б
динамика комплексного Иза для г. Оренбурга в условиях тумана: а – T > 0; б – T < 0
Эффективность решения во многом зависит от корректности выбора граничных условий. Кроме этого, нелинейность уравнений приводит к необходимости осреднения полученных уравнений для того, чтобы по возможности избежать появления моментов более высокого порядка. Для этого на определенном этапе расчетов применяют параметризацию неизвестных выражений.
Построенные в результате работы графики значительно упрощают процесс оценки качества атмосферы и прогнозирования экологической ситуации местности.
Проведенный анализ полученных результатов исследования позволяет заключить, что построенные геометрические модели являются поверхностями плоскопараллельного переноса, что существенно упрощает процесс исследования поведения тех или иных выходных параметров от задаваемых.
Рецензенты:Чепасов В.И., д.т.н., профессор кафедры информационных систем и технологий, заведующий кафедрой информационных систем и технологий, ФГБОУ ВПО «Оренбургский государственный университет», г. Оренбург;
Межуева Л.В., д.т.н., профессор кафедры пищевой биотехнологии, начальник патентного отдела управления научных исследований, ФГБОУ ВПО «Оренбургский государственный университет», г. Оренбург.
Работа поступила в редакцию 26.02.2014.