Металлы и сплавы являются основой большинства современных конструкционных материалов и передовых технологий. Сталь и полупроводники, драгоценные, редкие и тугоплавкие металлы используются в различных отраслях промышленности. Как и для ряда прочих товаров, мировые цены на металлы устанавливаются по результатам торгов на Лондонской бирже, Шанхайской фьючерсной бирже, Бразильской товарно-фьючерсной бирже, Токийской и Нью-Йоркской товарных биржах и др. Однако основной объем мировой торговли цветными металлами приходится на Лондонскую биржу металлов (LME). Так, по отчетным данным LME за 2013 г. биржа зарегистрировала рекордный объем торгов, составивший 171,1 млн лотов, что на 7,1 % больше, чем в 2012 г. Данный объем эквивалентен 4 млрд т или 14,6 трлн USD. В конце 2013 г. доля LME на глобальном рынке биржевых фьючерсов на металлы превысила 84 %. Цены, установленные на LME, определяются потребностями в производственном секторе и служат глобальными ориентирами при осуществлении сделок по купле-продаже металлов. Уровень и динамика цен на цветные металлы выступают важными ценообразующими факторами по широкому спектру товаров. При этом изменения спроса на отдельный металл определенным образом соответствуют колебаниям конъюнктуры рынков других металлов. В связи с этим весьма актуальным является изучение взаимозависимостей цен отдельных металлов, торгующихся на LME [5, 6].
Для анализа указанных зависимостей в рамках выполненной работы исследовались цены LME на основные цветные металлы, а также цены на драгметаллы и жидкие топливно-энергетические ресурсы (ТЭР) для выявления возможных дополнительных связей. Данные о ежедневных ценах анализировались за период с 01.01.2009 по 01.11.2013 включительно – всего 1766 значений. Первично из временных рядов цен на вышеназванные товары были удалены трендовые составляющие, сезонные и циклические компоненты и автокорреляция. Это позволило получить из них необходимые случайные величины, которые были в дальнейшем использованы для построения соответствующих регрессионных моделей [1, 7]
Так как значения по разным временным рядам отличались на порядок, их стандартизировали следующим образом:
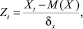 (1)
(1)
где Zt – стандартизированные значения временного ряда; Xt – нестандартизированные значения цен на выбранные товары в t-й день; M(X) – математическое ожидание значений ряда; δx – среднеквадратическое отклонение значений ряда.
Анализ автокорреляционной функции сезонные и циклические компоненты не выявил. Трендовая составляющая из «стандартизированных» рядов цен была удалена так:
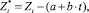 (2)
(2)
где a и b – коэффициенты линейной парной регрессии в уравнении 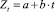 ;
; 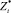 – значения, полученные из временного ряда после удаления тренда.
– значения, полученные из временного ряда после удаления тренда.
От автокорреляции избавлялись следующим образом:
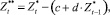 (3)
(3)
где 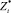 – значения временного ряда после удаления тренда;
– значения временного ряда после удаления тренда; 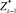 – значения временного ряда после удаления тренда, смещенные на один день назад; c и d – коэффициенты линейной парной регрессии в уравнении
– значения временного ряда после удаления тренда, смещенные на один день назад; c и d – коэффициенты линейной парной регрессии в уравнении 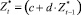 ;
; 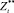 – стандартизированные случайные величины, полученные из временного ряда после удаления тренда и автокорреляции.
– стандартизированные случайные величины, полученные из временного ряда после удаления тренда и автокорреляции.
После удаления автокорреляции осталось 1765 значений каждой цены. Остаточные компоненты стали являться случайными величинами, над которыми в дальнейшем был проведен корреляционный анализ с помощью линейного критерия Пирсона (табл. 1).
Таблица 1
Парные коэффициенты корреляции цен анализируемых товаров на LME
|
Алюминий |
Медь |
Никель |
Олово |
Свинец |
Цинк |
Золото |
Серебро |
Платина |
Палладий |
Нефть Брент |
Нефть Лайт |
Мазут |
Бензин |
|
|
Алюминий |
1 |
|||||||||||||
|
Медь |
0,59 |
1 |
||||||||||||
|
Никель |
0,65 |
0,54 |
1 |
|||||||||||
|
Олово |
0,47 |
0,40 |
0,52 |
1 |
||||||||||
|
Свинец |
0,60 |
0,52 |
0,55 |
0,51 |
1 |
|||||||||
|
Цинк |
0,65 |
0,55 |
0,59 |
0,51 |
0,79 |
1 |
||||||||
|
Золото |
0,24 |
0,35 |
0,21 |
0,17 |
0,21 |
0,20 |
1 |
|||||||
|
Серебро |
0,33 |
0,46 |
0,31 |
0,27 |
0,28 |
0,27 |
0,76 |
1 |
||||||
|
Платина |
0,39 |
0,52 |
0,34 |
0,28 |
0,32 |
0,32 |
0,69 |
0,67 |
1 |
|||||
|
Палладий |
0,40 |
0,53 |
0,37 |
0,30 |
0,31 |
0,31 |
0,49 |
0,56 |
0,72 |
1 |
||||
|
Нефть Брент |
0,41 |
0,45 |
0,41 |
0,31 |
0,34 |
0,35 |
0,26 |
0,37 |
0,40 |
0,41 |
1 |
|||
|
Нефть Лайт |
0,42 |
0,52 |
0,38 |
0,31 |
0,34 |
0,33 |
0,27 |
0,39 |
0,43 |
0,45 |
0,82 |
1 |
||
|
Мазут |
0,38 |
0,46 |
0,38 |
0,29 |
0,33 |
0,32 |
0,25 |
0,36 |
0,41 |
0,41 |
0,87 |
0,80 |
1 |
|
|
Бензин |
0,32 |
0,38 |
0,30 |
0,23 |
0,24 |
0,26 |
0,20 |
0,32 |
0,34 |
0,36 |
0,75 |
0,69 |
0,74 |
1 |
По корелляционной матрице были построены корреляционные плеяды. На рисунке показаны наиболее сильные связи между ценами, выявленные в процессе анализа.
По корреляционным плеядам видно, что наибольшие коэффициенты корреляции между собой имеют цены товаров однородных групп. Это можно объяснить относительной синхронностью колебаний спроса на товары, имеющие схожее потребительское назначение. Однако весьма неожиданным является наличие связей примерно одинаковой силы всех трех товарных групп через цену меди. Выявление в результате статистического анализа подобного факта дает определенную возможность использовать цены LME на медь в качестве усредненного индикатора конъюнктурных колебаний как для рынков цветных, так и драгоценных металлов, а также жидких ТЭР. Объяснить данную зависимость можно статистически равновеликой чувствительностью спроса на медь к изменениям ситуации на рынках промышленных металлов, углеводородов и инвестиций в 2009–2013 гг. [8, 10, 11].
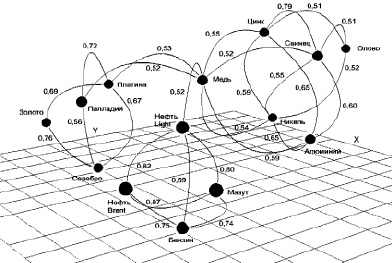
Корреляционные плеяды цен LME на металлы и углеводороды
На следующем этапе исследования при построении регрессионной зависимости между ценой LME на отдельный цветной металл и ценами на остальные цветные, драгоценные металлы и углеводороды для устранения мультиколлинеарности был использован метод главных компонент (МГК). Этот прием факторного анализа позволяет выявить непосредственно неизмеряемые факторы, в той или иной степени связанные с измеряемыми случайными величинами, и минимизировать корреляцию между этими скрытыми факторами. Собственно факторный анализ проводился с применением программы Statistica 8 [2].
Первой строилась регрессия для цены на алюминий. После процедуры анализа цен по МГК из 13 переменных (без цен на алюминий) было извлечено 3 фактора F1, F2 и F3, которые были повернуты по методу варимакс-вращения с нормализацией Кайзера. Анализ полученной матрицы компонент позволил разделить имеющиеся переменные по трем группам исходя из величины связей между ними. Результаты анализа представлены в табл. 2.
Таблица 2
Факторная структура для цены алюминия
|
F1 |
F2 |
F3 |
|
|
Медь |
0,324 |
0,582 |
0,409 |
|
Никель |
0,236 |
0,738 |
0,162 |
|
Олово |
0,130 |
0,676 |
0,124 |
|
Свинец |
0,123 |
0,851 |
0,126 |
|
Цинк |
0,129 |
0,869 |
0,114 |
|
Золото |
0,047 |
0,062 |
0,884 |
|
Серебро |
0,196 |
0,164 |
0,825 |
|
Платина |
0,232 |
0,206 |
0,836 |
|
Палладий |
0,284 |
0,253 |
0,701 |
|
Нефть Brent |
0,893 |
0,231 |
0,183 |
|
Нефть Light |
0,844 |
0,233 |
0,237 |
|
Мазут |
0,892 |
0,204 |
0,191 |
|
Бензин |
0,847 |
0,111 |
0,143 |
Как видно из табл. 2, в данном случае наибольшие нагрузки по фактору F1 дают цены LME на ТЭР, взаимосвязь между ними прямая. Поэтому фактор F1 был назван «энергетическим». Наибольшие нагрузки по фактору F2 дают цены цветных металлов, взаимосвязь между ними также прямая. Учитывая преимущественно производственное потребление цветных металлов, фактору F2 было присвоено название «производственный». И, наконец, наибольшие нагрузки по фактору F3 также с прямой связью привносят цены драгметаллов. Исходя из роли драгметаллов в экономике, фактор F3 был назван «финансовым». Идентифицированные факторы объединяют совокупность соответствующих однородных причин, обуславливающих конъюнктурные флуктуации на рынке алюминия (для прочих цветных металлов аналогично – см.далее). Используя выделенные факторы, была построена регрессионная модель зависимости цены LME на алюминий от F1, F2 и F3.
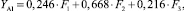 (4)
(4)
где F1 – энергетический фактор; F2 – производственный фактор; F3 – финансовый фактор; YAl – стандартизированная случайная величина, полученная из цены на алюминий после удаления из нее тренда и автокорреляции.
Регрессионный анализ показал, что величина коэффициента множественной корреляции R = 0,744 свидетельствует о высокой взаимосвязи между результатом и факторными признаками, а значение коэффициента детерминации R2 = 0,553 показывает, что включенные в модель факторы объясняют более половины вариации результативного признака – цены алюминия. Рассчитанное по коэффициенту детерминации (R2) значение критерия Фишера Fрасч = 726,2474 больше, чем табличное значение для уровня значимости α = 0,05 Fтабл(0,05; 3; 1761) = 2,6099, поэтому уравнение регрессии следует признать адекватным. Коэффициенты при переменных F1, F2 и F3 по t-критерию Стьюдента статистически значимы, поскольку для них tрасч = 15,424, tрасч = 41,925, tрасч = 13,534 соответственно больше по модулю для уровня значимости α = 0,05, чем tтабл(0,05; 1761) = 1,9613. Кроме того, по t-критерию Стьюдента свободный член уравнения (4) статистически незначим, т.к. tрасч = –1,7E–15 меньше по модулю для уровня значимости α = 0,05, чем tтабл(0,05; 1761) = 1,9613.
Из уравнения регрессии (4) видно, что энергетический и финансовый факторы оказывают в среднем в 3 раза меньшее влияние на движение цены алюминия, чем производственный фактор (0,668), что, очевидно, обусловлено формированием спроса на алюминий в основном на рынках производственных товаров.
Аналогичным образом был выполнен факторный анализ для цен LME на остальные цветные металлы – медь, никель, олово, свинец, цинк. Данные о факторной нагрузке на цены этих металлов по компонентам для каждого из них приведены в табл. 3-7.
Таблица 3
Факторная структура для цены меди
|
F1 |
F2 |
F3 |
|
|
Алюминий |
0,228 |
0,769 |
0,197 |
|
Никель |
0,229 |
0,754 |
0,157 |
|
Олово |
0,131 |
0,661 |
0,134 |
|
Свинец |
0,122 |
0,837 |
0,130 |
|
Цинк |
0,126 |
0,865 |
0,114 |
|
Золото |
0,048 |
0,071 |
0,889 |
|
Серебро |
0,197 |
0,167 |
0,827 |
|
Платина |
0,233 |
0,211 |
0,835 |
|
Палладий |
0,285 |
0,253 |
0,697 |
|
Нефть Brent |
0,892 |
0,239 |
0,183 |
|
Нефть Light |
0,844 |
0,234 |
0,233 |
|
Мазут |
0,892 |
0,206 |
0,190 |
|
Бензин |
0,846 |
0,121 |
0,142 |
Таблица 4
Факторная структура для цены никеля
|
F1 |
F2 |
F3 |
|
|
Алюминий |
0,758 |
0,234 |
0,200 |
|
Медь |
0,592 |
0,323 |
0,401 |
|
Олово |
0,656 |
0,136 |
0,124 |
|
Свинец |
0,856 |
0,124 |
0,118 |
|
Цинк |
0,881 |
0,129 |
0,105 |
|
Золото |
0,066 |
0,047 |
0,884 |
|
Серебро |
0,163 |
0,197 |
0,826 |
|
Платина |
0,215 |
0,232 |
0,834 |
|
Палладий |
0,258 |
0,284 |
0,700 |
|
Нефть Brent |
0,227 |
0,894 |
0,182 |
|
Нефть Light |
0,238 |
0,844 |
0,235 |
|
Мазут |
0,199 |
0,893 |
0,191 |
|
Бензин |
0,116 |
0,846 |
0,142 |
Как видно из таблиц, выделенные факторы четко сохраняют свою нагрузку по компонентам, однако в структуре скользят по порядку наименования. Поэтому для построения регрессии и сохранения единообразия было произведено переобозначение факторов при сохранении их первичного поименования: Ф1 – энергетический фактор, определяющий вариацию цен LME на цветные металлы в зависимости от конъюнктурных колебаний на рынках жидких энергоресурсов; Ф2 – производственный фактор, определяющий вариацию цен LME на цветные металлы в зависимости от конъюнктурных колебаний на рынках производственных товаров (в данном исследовании – на рынках самих же цветных металлов – прим.авт.); Ф3 – финансовый фактор, определяющий вариацию цен LME на цветные металлы в зависимости от конъюнктурных колебаний на рынках финансовых активов.
Таблица 5
Факторная структура для цены олова
|
F1 |
F2 |
F3 |
|
|
Алюминий |
0,218 |
0,790 |
0,190 |
|
Никель |
0,312 |
0,612 |
0,398 |
|
Олово |
0,225 |
0,756 |
0,152 |
|
Свинец |
0,116 |
0,840 |
0,121 |
|
Цинк |
0,118 |
0,878 |
0,105 |
|
Золото |
0,047 |
0,068 |
0,884 |
|
Серебро |
0,198 |
0,159 |
0,827 |
|
Платина |
0,229 |
0,222 |
0,832 |
|
Палладий |
0,281 |
0,263 |
0,698 |
|
Нефть Brent |
0,892 |
0,237 |
0,181 |
|
Нефть Light |
0,842 |
0,241 |
0,236 |
|
Мазут |
0,891 |
0,210 |
0,190 |
|
Бензин |
0,846 |
0,123 |
0,142 |
Таблица 6
Факторная структура для цены свинца
|
F1 |
F2 |
F3 |
|
|
Алюминий |
0,208 |
0,182 |
0,805 |
|
Медь |
0,306 |
0,393 |
0,618 |
|
Олово |
0,206 |
0,138 |
0,795 |
|
Свинец |
0,116 |
0,113 |
0,677 |
|
Цинк |
0,128 |
0,113 |
0,825 |
|
Золото |
0,052 |
0,887 |
0,059 |
|
Серебро |
0,196 |
0,825 |
0,169 |
|
Платина |
0,229 |
0,832 |
0,223 |
|
Палладий |
0,274 |
0,692 |
0,286 |
|
Нефть Brent |
0,890 |
0,180 |
0,244 |
|
Нефть Light |
0,841 |
0,233 |
0,250 |
|
Мазут |
0,892 |
0,190 |
0,210 |
|
Бензин |
0,845 |
0,141 |
0,129 |
Результаты построения моделей линейной множественной регрессии, проведенного аналогично построению модели для алюминия, представлены в табл. 8 и 9. Как видно из указанных таблиц, коэффициенты множественной корреляции R в уравнениях свидетельствуют о высокой взаимосвязи между результатами Yi и факторными признаками Ф1, Ф2 и Ф3. Следует подчернуть, что для цен LME на олово величина связи в соответствии с величиной R в уравнении (8) несколько меньше, чем для прочих металлов, однако по шкале Чеддока считается заметной [4].
Таблица 7
Факторная структура для цены цинка
|
F1 |
F2 |
F3 |
|
|
Алюминий |
0,213 |
0,184 |
0,791 |
|
Медь |
0,309 |
0,394 |
0,610 |
|
Никель |
0,208 |
0,136 |
0,792 |
|
Олово |
0,110 |
0,105 |
0,696 |
|
Свинец |
0,126 |
0,129 |
0,791 |
|
Золото |
0,052 |
0,888 |
0,059 |
|
Серебро |
0,195 |
0,824 |
0,176 |
|
Платина |
0,229 |
0,832 |
0,224 |
|
Палладий |
0,274 |
0,691 |
0,288 |
|
Нефть Brent |
0,891 |
0,179 |
0,243 |
|
Нефть Light |
0,839 |
0,232 |
0,255 |
|
Мазут |
0,890 |
0,188 |
0,216 |
|
Бензин |
0,848 |
0,143 |
0,120 |
Значения коэффициентов детерминации R2 говорят о том, что включенные в модель факторы объясняют более половины вариации результативного признака для алюминия, меди, никеля, свинца, цинка и более трети для олова. Так как рассчитанные по коэффициенту детерминации R2 значения F-критерия Фишера для анализируемых цен LME на цветные металлы (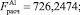
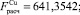
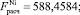
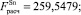
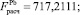
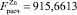 ) больше, чем табличное значение для уровня значимости α = 0,05 (Fтабл(0,05; 3; 1761) = 2,6099), то уравнения регрессии следует признать адекватными.
) больше, чем табличное значение для уровня значимости α = 0,05 (Fтабл(0,05; 3; 1761) = 2,6099), то уравнения регрессии следует признать адекватными.
Из табл. 9 видно, что по критерию Стьюдента свободные коэффициенты уравнения регрессии статистически незначимы, поскольку 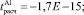
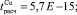
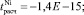
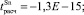
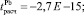
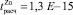 меньше по модулю для уровня значимости α = 0,05, чем tтабл(0,05; 1761) = 1,9613. Коэффициенты при факторных переменных статистически значимы для всех металлов, поскольку рассчитанные значения критерия Стьюдента для Φ1, Φ2 и Φ3 больше по модулю для уровня значимости α = 0,05, чем соответствующие табличные значения по каждому металлу.
меньше по модулю для уровня значимости α = 0,05, чем tтабл(0,05; 1761) = 1,9613. Коэффициенты при факторных переменных статистически значимы для всех металлов, поскольку рассчитанные значения критерия Стьюдента для Φ1, Φ2 и Φ3 больше по модулю для уровня значимости α = 0,05, чем соответствующие табличные значения по каждому металлу.
Поэтому уравнения линейной множественной регрессии принимают вид:
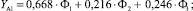 (5)
(5)
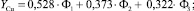 (6)
(6)
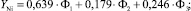 (7)
(7)
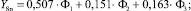 (8)
(8)
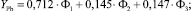 (9)
(9)
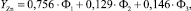 (10)
(10)
где Φ1 – фактор рынка производственных товаров; Φ2 – фактор рынка финансовых активов; Φ3 – фактор рынка ТЭР; YMe – стандартизированные случайные величины, полученные из цен LME на алюминий, медь, никель, олово, свинец и цинк после удаления из них тренда и автокорреляции.
Таблица 8
Характеристики регрессионных моделей для алюминия, меди, никеля, олова, свинца и цинка
|
Алюминий |
Медь |
Никель |
Олово |
Свинец |
Цинк |
|
|
Множественный коэффициент корреляции R |
0,744 |
0,723 |
0,708 |
0,554 |
0,742 |
0,781 |
|
Коэффициент детерминации R2 |
0,553 |
0,522 |
0,501 |
0,307 |
0,550 |
0,609 |
|
Стандартная ошибка |
0,669 |
0,692 |
0,707 |
0,833 |
0,671 |
0,626 |
|
Наблюдения |
1765 |
1765 |
1765 |
1765 |
1765 |
1765 |
Таблица 9
Коэффициенты уравнений линейной множественной регрессии
|
Для цен на алюминий |
Для цен на медь |
Для цен на никель |
||||
|
Коэффициенты |
Значение |
t-критерий |
Значение |
t-критерий |
Значение |
t-критерий |
|
Свободный член а0 |
–2,7 E–17 |
–1,7 E–15 |
9,4 E–17 |
5,7 E–15 |
–2,3 E–17 |
–1,4 E–15 |
|
а1 при Ф1 |
0,668 |
41,925 |
0,528 |
32,068 |
0,639 |
37,940 |
|
а2 при Ф2 |
0,216 |
13,534 |
0,373 |
22,665 |
0,179 |
10,629 |
|
а3 при Ф3 |
0,246 |
15,424 |
0,322 |
19,545 |
0,246 |
14,592 |
|
Для цен на олово |
Для цен на свинец |
Для цен на цинк |
||||
|
Коэффициенты |
Значение |
t–критерий |
Значение |
t–критерий |
Значение |
t–критерий |
|
Свободный член а0 |
–2,5 E–17 |
–1,3 E–15 |
–4,3 E–17 |
–2,7 E–15 |
1,9 E–17 |
1,3 E–15 |
|
а1 при Ф1 |
0,507 |
25,562 |
0,712 |
44,545 |
0,756 |
50,746 |
|
а2 при Ф2 |
0,151 |
7,599 |
0,145 |
9,081 |
0,129 |
8,675 |
|
а3 при Ф3 |
0,163 |
8,214 |
0,147 |
9,215 |
0,146 |
9,827 |
Таким образом, по результатам исследований можно сделать следующие выводы. Во-первых, построенные уравнения регрессии показывают, что за анализируемый период с 01.01.2009 по 01.11.2013 г. в среднем более половины вариаций цен цветных металлов объяснялось отобранными факторами. При этом наиболее низкий коэффициент детерминации имеет уравнение (8) для цен олова, что, вероятно, объясняется высоким уровнем монополизации рынка данного металла [3]. Во-вторых, наибольшее влияние на изменение цены отдельного цветного металла оказывали цены прочих металлов, рассматриваемых в данном исследовании. В среднем влияние фактора Ф1 в ~3 раза сильнее каждого из двух других факторов. Это, по-видимому, объясняется особенностями групповой динамики цен на цветные металлы, отражающей их потребление в той или иной фазе экономического цикла [9]. В-третьих, наиболее равномерно влияние факторов распределено в уравнении (6) для меди, что соответствует связям, отраженным в корреляционных плеядах на рисунке. Это, по мнению авторов, дает возможность использовать цены LME на медь как первичный индикатор конъюнктурных колебаний на рынках цветных и драгоценных металлов, а также энергоресурсов [12].
Вероятно, распределение влияния обозначенных факторов на изменения цен цветных металлов носит устойчивый характер и сохранится в будущем. Однако, для подтверждения этого нужны дополнительные прогностические исследования.
Рецензенты:
Попов В.Л., д.э.н., профессор кафедры «Менеджмент и маркетинг», ФГБОУ ВПО Пермский национальный исследовательский политехнический университет, г. Пермь;
Елохова И.В., д.э.н., профессор кафедры «Управление финансами», ФГБОУ ВПО Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 06.03.2014.



