Известно, что в формировании электронных свойств магнитных полупроводников важную роль играют флуктуации спиновой плотности [2–5]. С помощью спин-флуктуационной теории полупроводников и полуметаллических соединений переходных металлов авторы [2] показали, что исходный электронный спектр расщепляется флуктуирующими обменными полями, при этом рост с температурой амплитуды спиновых флуктуаций в рассматриваемой системе электронов приводит к подавлению щели не только в d-, но и в sp-зонах.
Однако предложенный подход позволяет описать только равновесные электронные превращения в магнитных полупроводниках [2, 6, 7], которые отличаются плавным температурным возрастанием электропроводности, сопровождаемым формированием промежуточного состояния с исчезающе малым значением ТКС, а в сильных электрических полях электронный фазовый переход полупроводник‒металл носит неравновесный характер.
В данной работе развитая ранее спин-флуктуационная теория дополняется учетом влияния на флуктуации спиновой плотности внешних электрических полей (за счет явления саморазогрева). При этом учитывается, что внутренняя температура полупроводника T′, находящегося в условиях саморазогрева, зависит от плотности тока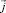 
и приложенной разности потенциалов ∆j, и определяется из условия динамического равновесия
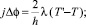(1)
здесь T – температура окружающей среды, отличная от внутренней температуры образца Т′, l – коэффициент теплопроводности полупроводника, постоянный по всей толщине образца h.
Используя условие электронейтральности, показано, что плотность состояний как sp-, так и d-электронов претерпевает спин-флуктуационные перенормировки и в отсутствие ферромагнитного упорядочения имеет вид
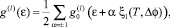(2)
где g0(l)(e) – плотность состояний невзаимодействующих sp-(l = s) или d-(l = d) электронов, ξl(Т, ∆j) – величина спин-флуктуационного расщепления энергетического спектра sp- или d-электронов, зависящая (в условиях саморазогрева) от температуры (T) и приложенной разности потенциалов (∆j).
С учетом полученных в [2] результатов для ξl(Т′) и условия (1) имеем, что амплитуда спиновых флуктуаций становится зависящей от приложенного напряжения и плотности тока, текущего по образцу:
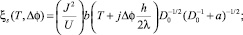(3)
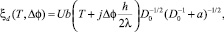(4)
где U – параметр внутриатомного кулоновского отталкивания d-электронов, J – параметры sp, d-обменного взаимодействия, D0 – фактор обменного усиления однородной магнитной восприимчивости d-электронов, a и b – коэффициенты, определяющиеся из нейтронографических данных или из данных магнитных измерений [2].
Последнее приводит к трансформации электронного спектра при изменении ∆j и j, а также к зависимостям от напряжения и плотности тока других физических величин (в частности фактора обменного усиления однородной магнитной восприимчивости d-электронов – D0, химического потенциала – m, плотности электронных состояний, ширины запрещенной зоны – Eg и т.д.). При этом в отличие от обычных полупроводников, влияние напряжения и плотности тока на свойства магнитных полупроводников оказывается значительно усиленным из-за большой величины фактора обменного усиления.
Саморазогрев образца ведет не только к тривиальному увеличению термически активированных носителей тока, но и перестройке всего электронного спектра и, как следствие, к еще более сильному изменению плотности тока. Для самосогласованного описания зависимости плотности электронных состояний sp,d-электронов от приложенного к образцу напряжения почти магнитных полупроводников система уравнений (1)–(4) дополняется уравнениями для плотности тока и теплопроводности
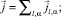
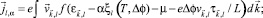(5)
здесь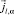 
– плотности тока каждой из групп sp-(l = s) или d-(l = d) электронов, 
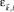– энергия электронов с квазиимпульсом 
; 
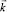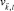– проекция скорости электронов на направление электрического поля, a = ±1, 
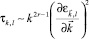– время релаксации; fF(ε – μ) – функция Ферми-Дирака; m – химический потенциал, определяющийся из условия электронейтральности; r – параметр, равный 3/2 в случае рассеяния электронов на фононах;
l = lфон + λd, (6)
где l = lфон – фононный вклад в теплопроводность; λd – вклад d-электронов, определяющийся согласно закону Видемана-Франса как произведение теплоемкости на проводимость, а выражение для проводимости возьмем из работы [1]. Таким образом, теплопроводность d-электронов может быть записана в виде
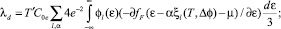(7)
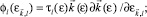
здесь fF(e – m) – функция Ферми-Дирака; m – химический потенциал, определяющийся из условия электронейтральности; C0e – одноэлектронная теплоемкость, перенормированная флуктуациями
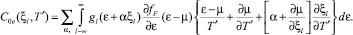(8)
Система уравнений (1)–(8) позволяет корректно описать плотность электронных состояний магнитных полупроводниковых соединений, находящихся в условиях саморазогрева под действием сильных электрических полей. Эффект саморазогрева будет дополнительно усиливаться сужением энергетической щели в спектре таких полупроводников. Однако аналитическое решение этой системы уравнений в общем случае невозможно. Поэтому данная система была решена численно на примере FeSi. При вычислении плотности электронных состояний использовались значения спин-флуктуационных параметров a = 0 и b = 10/U, значение sp,d-обмена– J = 0,1U, найденные в [2] из анализа нейтронографических данных.
а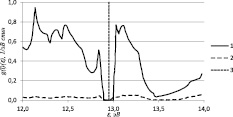 
б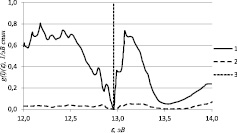 
в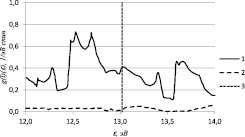 
Рис. 1. Плотность электронных состояний FeSi: 1 – соответствует d-электронам; 2 – sp-электронам; 3 – положение химического потенциала. Температура окружающей среды T = 50 K: а – ∆j = 0В, саморазогрев отсутствует; б – ∆j = 0,18В; в – ∆j = 0,23В
В работе [2] показано, что рост температуры исследуемого соединения приводит к наблюдаемому на эксперименте при Т′ ~ 100 K электронному фазовому переходу из полупроводникового в металлическое состояние, который обусловлен ростом тепловых спиновых флуктуаций, ведущих к «схлопыванию» энергетической щели в спектре d-электронов и смещению химического потенциала в область делокализованных состояний. В свою очередь химический потенциал (из-за несимметричности d-зон) начинает смещаться влево по шкале энергий и при Т′ ≈ 200 K попадает в валентную зону sp-электронов, вследствие чего состояние последних также становится металлическим. Таким образом, при внутренних температурах образца ниже 100 К проводимость моносилицида железа формируется только за счет активационного механизма, в интервале от 100 и до 200 К – металлического и активационного одновременно, а выше 200 К – только металлического [2].
Анализ результатов численных расчетов плотности электронных состояний sp,d-электронов показывает, что под действием внешних электрических полей металлизация образца происходит при значительно более низких температурах окружающей среды.
Графики плотности электронных состояний FeSi, находящегося в условиях саморазогрева под действием электрических полей, приведены на рис. 1 и 2. В отсутствии внешнего электрического поля при температуре окружающей среды T = 50 K в спектре как d-, так и sp-электронов имеется энергетическая щель (рис. 1, а) и реализуется активационная проводимость, что согласуется с экспериментом и работой [2, 7]. Рост напряжения, приложенного к образцу, приводит к постепенному сужению энергетической щели в спектре d-электронов. Из рис. 1, б видно, что при температуре окружающей среды T = 50 K энергетическая щель исчезает уже при значении приложенного напряжения ∆j ≈ 0,18 В. Дальнейший рост напряжения приводит к схлопыванию энергетической щели и в спектре sp-электронов – при ∆j ≈ 0,23 В, а также перестройке всего электронного спектра (рис. 1, в).
а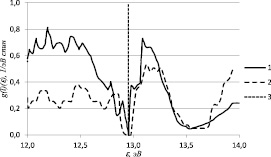 
б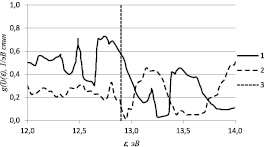
Рис. 2. Плотность электронных состояний FeSi: 1 – соответствует d-электронам; 2 – sp-электронам, умноженная на 10; 3 – положение химического потенциала. Температура окружающей среды T = 100 K: а – ∆j = 0В, саморазогрев отсутствует; б – ∆j = 0,14В
Рис. 2 демонстрирует плотность электронных состояний FeSi, находящегося в условиях саморазогрева под действием электрических полей при температуре окружающей среды T = 100 K. Как известно, при этой температуре состояние d-электронов сразу является металлическим (рис. 2, а), щель в sp-спектре не исчезает. С увеличением внешнего электрического поля, вследствие саморазогрева образца, химический потенциал начинает смещаться влево по шкале энергий и при ∆j ≈ 0,14 В попадает в валентную зону sp-электронов (рис. 2,б), что ведет к тому, что состояние sp-электронов металлизируется. При этом энергетическая щель в спектре sp-электронов не исчезает, хотя и продолжает сужаться. Дальнейшее увеличение напряжения до ∆j ≈ 0,16 В приводит к схлопыванию энергетической щели и в спектре sp-электронов. Полученные при этом плотности состояний d- и sp-электронов имеют такой же вид, как на рис. 1,в, что объясняется совпадением внутренних температур образца (при T = 50 K, ∆j ≈ 0,23 В и T = 100 K, ∆j ≈ 0,16 В).
Таким образом, на основе спин-флуктуационной теории развит подход, позволяющий описать влияние саморазогрева под действием сильных электрических полей на плотность электронных состояний магнитных полупроводников на примере FeSi. Показано, что выделение тепла, вследствие протекания тока, обусловливает рост амплитуды спиновых флуктуаций и расщепление ими электронных спектров, что в свою очередь ведет к схлопыванию энергетической щели.
Рецензенты:
Чикова О.А., д.ф.-м.н., профессор, зав. кафедрой технологии, ФГБОУ ВПО «Уральский государственный педагогический университет», г. Екатеринбург;
Сидоренко Ф.А., д.ф.-м.н., профессор кафедры физики, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 06.03.2014.