В современном научном мире нередко можно встретить случаи, когда при проведении наблюдений над одними и теми же объектами различные исследователи получают данные, существенно отличающиеся друг от друга [1]. Не является исключением и мониторинг экзогенных процессов (например, карстовых и суффозных) [4, 7, 8]. Это связано с рядом причин. Во-первых, разные исследователи при наблюдении за одними и теми же параметрами могут использовать различные методики. Во-вторых, могут использоваться различные приборы, отличающиеся точностью и погрешностью измерений. В-третьих, при проведении исследований могут возникать ошибки вследствие воздействия помех, неправильной работы оборудования и человеческого фактора [6].
Возникает проблема согласования и обработки данных, полученных из различных источников (исследователей). Особо остро проблема стоит в том случае, когда разные источники дают неполные данные (с разной периодичностью, с наличием пропусков за определенные периоды и т.д.).
Цель работы – рассмотреть особенности согласования и обработки данных, полученных из различных источников при проведении мониторинга экзогенных процессов.
Несогласованность данных
В 2013 году в ходе выполнения гранта РФФИ № 13-07-97510 проводились исследования влияния подземных вод на развитие экзогенных процессов [9]. Была проведена оценка состояния поверхностных и подземных вод округа Муром. В качестве основы для исследований были использованы данные, непосредственно полученные на кафедре техносферной безопасности МИ ВлГУ, данные Санитарно-гигиенического мониторинга Муромского района, сведения Роспотребнадзора и МУП «Водопровод и канализация». При анализе данных возникли некоторые сложности. Оказалось, что данные из разных источников плохо стыкуются друг с другом.
а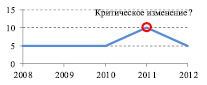 
б
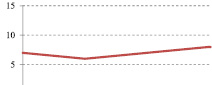
Рис. 1. Значения одного из параметров наблюдений за экзогенными процессами по данным различных источников: а – источник 1; б – источник 2
На рис. 1, а приведено изменение показателя «Цветность» воды (измеряемого в градусах) по данным одного из источников. Как можно заметить, в 2011 году наблюдается существенный рост показателя (в 2 раза). Это может свидетельствовать о неких критических изменениях в режиме подземных вод и их влиянии на развитие экзогенных процессов. Однако при детальном анализе оказывается, что измерение параметра осуществляется с шагом 5 градусов. Таким образом, фактически произошло изменение на один шаг измерения. Анализ данных другого источника (рис. 1, б) для этого же показателя продемонстрировал иную картину. Шаг измерения этого источника составляет 1 градус. Как можно заметить, резких изменений показателя в 2011 году не наблюдается. Фактически колебания составили 1 градус (с 7 в 2010 году до 8 в 2011). Таким образом, округления значений в первом случае при большом шаге измерений могут привести к ошибочным выводам.
Согласование данных
Пусть данные получаются из двух источников информации D1 и D2.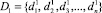 
, 
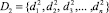, где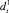 
– данные наблюдений источника D1 за i-й период, 
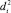– данные наблюдений источника D2 за i-й период (см. рис. 2). На практике данные источников за i-й период могут не совпадать друг с другом, т.е. 
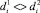[3].
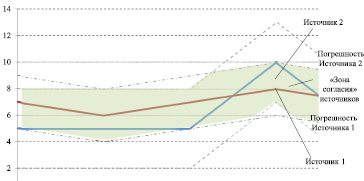
Рис. 2. Данные, полученные из разных источников
Каждый источник информации может иметь свои погрешности измерений (вызванные используемым оборудованием и методами исследования) [2]. Обозначим погрешность измерений источника D1 как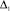 
, погрешность источника D2 как 
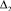. Тогда фактическое значение параметров от источника D1 будет лежать в диапазоне 
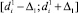(«зоне погрешности»), от источника D2 в диапазоне 
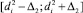. Другими словами, для каждого наблюдения можно задать как полученное значение, так и диапазон, в пределах которого могут быть отклонения этого значения от реальной (фактической) величины.
Данные, поступающие от каждого источника, имеют определенный шаг изменения значений. Это связано с ограничениями шкалы измерений приборов (последний учитываемый знак), особенностями используемой методики исследования и т.д. Шаг может варьироваться в больших пределах в зависимости от вида исследуемого параметра. Обозначим s1 шаг измерений источника D1, s2 – шаг источника D2. Шаг измерений можно связать с погрешностями источников: погрешность должна составлять не менее половины шага измерения, т.е.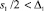 
и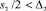 
.
Пересечение диапазонов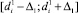 
и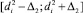 
дает «зону согласия» [5]. Таким образом
,
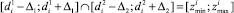где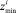 
и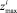 
– нижняя и верхняя границы «зоны согласия» для i-го периода.
При отсутствии ошибок значения обоих источников D1 и D2 для i-го периода будут лежать в «зоне согласия». Фактическое значение параметров также будет лежать в этой области. Это позволяет сузить область фактических значений.
В случае, если диапазоны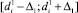 
и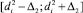 
не пересекаются, либо значения не входят в «зоны согласия», т.е. 
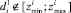или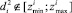 
, можно говорить о наличии ошибок в значениях одного из источников. Определить, какой же из источников содержит значения с ошибками, можно, например, вычислив тренд изменения значений и найдя наибольшее отклонение от него.
При необходимости совместного использования данных, полученных из нескольких источников (например, для заполнения пропусков в периодичности наблюдений), возникает вопрос: как объединить данные? Можно ли просто взять недостающие данные из разных источников и использовать их без предварительной обработки и корректировки? Чаще всего – нет. Пример рис. 1 показал, насколько могут отличаться данные. По этой причине необходима выработка более продуктивного подхода.
Для обеспечения возможностей использования данных из различных источников предлагается использование следующего решения [3, 5]. Вместо того чтобы использовать непосредственное значение показателя, взятого из того или иного источника, мы предлагаем использовать тройку «значение, погрешность, шаг измерения»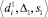 
, преобразовывая их при необходимости к единым единицам измерения (например, из г/м3 в мг/дм3). Такое решение позволяет собрать достаточно полную информацию об исследуемых процессах и обеспечить достаточную адекватность данных, собранных из различных источников, фактическому состоянию.
Рассмотрим алгоритм согласования данных мониторинга. В общем виде его можно представить следующим образом:
- Преобразование данных различных источников к одинаковым единицам измерения.
- Определение для каждого j-го источника погрешности измерения Δj.
- Определение для каждого j -го источника шага измерения sj.
- Преобразование данных в тройку «значение, погрешность, шаг измерения»
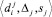. - Определение «зоны согласия» источников
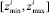, где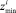 
– нижняя граница «зоны согласия» для i-го периода, 
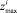– верхняя граница «зоны согласия» для i-го периода. - Проверка корректности данных (попадания значений в «зону согласия»)
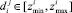. - Корректировка данных источников в случае необходимости (если
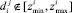). - Приведение данных с разной точностью к единой точности и порядку.
Выявление значимых изменений наблюдаемого параметра
Допустим, что имеется ряд наблюдений параметра за определенный n-й период. Данные наблюдений собраны из разных источников. Возникает вопрос: как выявить значимые изменения параметра в n + 1 период при наличии данных из разных источников за предшествующие периоды? Алгоритм выявления значимых изменений наблюдаемого параметра можно представить следующим образом [3].
- Составление троек «значение, погрешность, шаг измерения»
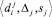для n предшествующих периодов для всех источников. - Получение тройки
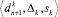для n + 1 периода от источника k. - Расчет «зон согласия» источников за n предшествующих периодов.
- Проверка, существуют ли случаи невхождения данных от источника k в «зону согласия», т.е.
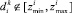. Если да – источник недостаточно надежен. Требуются дополнительные наблюдения. - Проверка, имеются ли тройки
, 
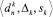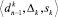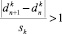, … для предшествующих периодов. Если да – переход к п. 6, иначе – п. 7. - Если
или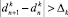 
, то произошли значимые изменения параметра наблюдения. - Поиск источника l с минимальным значением
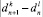. - Если sk ≥ sl, вычисляем
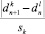, иначе вычисляем 
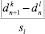. Если полученное значение больше 1, то произошли значимые изменения параметра наблюдения. - Если при Δk ≥ Δl верно
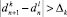, или при Δk < Δl верно 
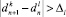, то произошли значимые изменения параметра наблюдения.
Заключение
Использование тройки «значение, погрешность, шаг измерения» позволяет осуществлять более точное согласование данных. Кроме того, это позволяет совместно использовать данные из различных источников с учетом их специфики. Анализ информации с учетом погрешностей позволяет, с одной стороны, исключить ошибочные выводы о значительных изменениях некоторых параметров наблюдений, а с другой стороны, выявить существенные закономерности в развитии экзогенных процессов. Предлагаемый подход не ограничивается экзогенными процессами и может использоваться в мониторинге других природных процессов и явлений.
Работа выполнена при поддержке гранта РФФИ № 13-07-97510 р_центр_а.
Рецензенты:
Жизняков А.Л., д.т.н., профессор, первый заместитель директора, Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Муром;
Орлов А.А., д.т.н., доцент, заведующий кафедрой «Физика и прикладная математика», Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Муром.
Работа поступила в редакцию 06.03.2014.