Развитие космической техники и высотной гиперзвуковой авиации требует развития методов определения аэродинамических характеристик (АДХ) во всем диапазоне режимов течения – от орбитального полета до посадочного режима. Обтекание космического аппарата (КА) на высотах ниже 60–70 км происходит в условиях сплошной среды. Числа Кнудсена в этих условиях достаточно малы (Kn << 1). Для исследования сплошносредных течений используются континуальные методы. Между этими предельными режимами КА проходит переходной режим обтекания, когда необходимо учитывать как столкновения молекул набегающего потока с поверхностью, так и межмолекулярные столкновения. Переходной режим характеризуется числами Кнудсена: 0,001 ≤ Kn ≤ 10. В этих условиях сплошносредные методы исследования неприменимы вследствие высокой разреженности и термохимической неравновесности газа [6]. Экспериментальное моделирование высокоскоростных разреженных течений довольно проблематично, и в настоящее время практически единственным средством получения информации об аэродинамической обстановке около КА на больших высотах полета являются методы вычислительной аэродинамики [1, 9]. Для анализа аэродинамических характеристик КА в переходном режиме необходимо использовать кинетический подход (решение уравнения Больцмана или его моделей). Математическое моделирование аэродинамики КА в переходном режиме является весьма сложным и требует больших вычислительных и временных ресурсов.
Компьютерное моделирование позволяет при помощи физических моделей и математических методов быстро проводить анализ аэродинамических характеристик гиперзвуковых летательных аппаратов. В настоящее время существует несколько подходов решения аэродинамических характеристик гиперзвуковых летательных аппаратов, и также проведены многочисленные исследования аэродинамических характеристик космических аппаратов вдоль всей траектории [4, 6, 7]. Однако метод Монте-Карло обладает достаточно хорошей точностью, но требует большого времени для вычисления. Другие основы на упрощенных инженерных методиках требуют малых затрат расчетного времени. Целью настоящей работы является анализ методов моделирования аэродинамических характеристик воздушно-космических аппаратов в переходном режиме.
Методы расчета аэродинамических характеристик тел в переходном режиме
В настоящее время условно можно выделить два инженерных подхода к вычислению аэродинамических характеристик по числам Рейнольдса. Первый подход состоит в построении функции аппроксимации при известных предельных значениях: свободномолекулярного С(0) и сплошносредного, обычно моделируемого по методу Ньютона С(∞).
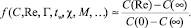
Функция f зависит от свойств газа, параметров набегающего потока, геометрии поверхности и др. В данной работе используется классический метод локальности и предполагается [4]
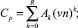
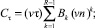
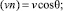
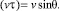
В предельном случае сплошной среды по методу Ньютона получаем
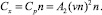
В другом предельном свободномолекуляном случае получаем
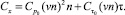
В данной работе используются выражения для элементарных сил давления и трения в форме работы [3].
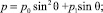
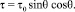
Здесь коэффициенты p0, p1, t0 (коэффициенты режима течения) зависят от числа Рейнольдса Re0 = r∞u∞L/m0, температурного фактора tw = Tw/T0, коэффициентов аккомодации и отношения удельных теплоемкостей c, L – характерный размер, m = m(T0) – коэффициент вязкости, T0, Tw – температура торможения и температура поверхности.
Зависимость коэффициентов режима в гиперзвуковом случае должна обеспечивать переход к свободномолекулярным значениям при Re0 → 0 и значениям теории Ньютона, методов тонких касательных клиньев или конусов при Re0 → ∞. На основе анализа расчетных и экспериментальных данных предложены эмпирические формулы
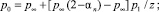
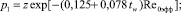
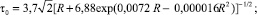
здесь
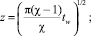
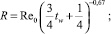
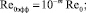
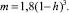
где h – относительные поперечные размеры аппарата, равные отношению его высоты к длине.
Предложенная методика хорошо зарекомендовала себя для расчета гиперзвукового обтекания выпуклых не очень тонких и пространственных тел. Расчет полностью отражает качественное поведение Сx в зависимости от разреженности среды во всем диапазоне углов атаки и дает количественное соответствие с экспериментом и расчетом по уравнению Больцмана с точностью около 5 %.
О точности соотношений локального метода можно сказать следующее. Ясно, что они применимы с наименьшей погрешностью в случае тел, близких к сфере, и неприменимы в случае очень тонких тел, когда не выполняется условие M∞ sin q >> 1. В рассматриваемых методах не учитывается влияние взаимодействия пограничного слоя с гиперзвуковым невязким потоком при больших числах Rе0. Расчетные и экспериментальные значения Cх конуса в переходном режиме согласуются удовлетворительно, данные по Cy согласуются значительно хуже. Необходимо подчеркнуть, что предложенная методика качественно верно отражает немонотонность зависимости Cy конуса от Rе0. Расчетные и экспериментальные результаты по Cх при a = 10° и 15° для пластины хорошо согласуются, данные же для Cх при a = 5° и Cy согласуются плохо. Это является следствием неучтенного в локальном методе влияния взаимодействия пограничного слоя с невязким потоком.
Таким образом, локальный метод расчета аэродинамических характеристик тел в гиперзвуковом потоке разреженного газа в переходном режиме дает хороший результат по Cх для широкого класса тел и качественно верный результат по Cy. При малых углах атаки (a < 5°) точность результата ухудшается, в этом случае необходимо привлекать более полные модели, учитывающие наличие пограничного слоя [1, 3, 6, 8].
Результаты исследования и их обсуждения
На рисунках представлены зависимости коэффициентов сил сопротивления Cx, подъемной Cy и момента тангажа mz от угла атаки (a = 0–90°) при различных значениях числа Рейнольдса Re. Параметры задачи были следующие: отношение теплоемкостей g = 1,4, температурный фактор tw = Tw/T0 = 0,4, скоростное отношение s = 10, число Рейнольдса Rе0 = 0, 10, 102, 104.
На рис. 2–4 представлены сравнения результатов зависимости Cx(a), Cy(a), mz(a) для воздушно-космического аппарата (ВКА) «Клипер», модель ЦАГИ [2], и гиперзвукового летательного аппарата (ГЛА) «Falcon HTV-2» (рис. 1) с помощью локального метода.


Рис. 1. Расчетные схемы ВКА «Клипер» и ГЛА «Falcon HTV-2»
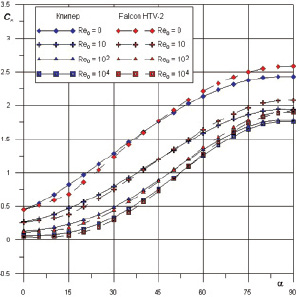
Рис. 2. Зависимость Cx(a) для «Клипер» и «Falcon HTV-2»
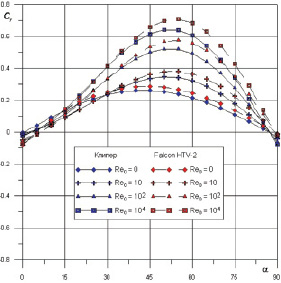
Рис. 3. Зависимость Cy(a) для «Клипер» и «Falcon HTV-2»
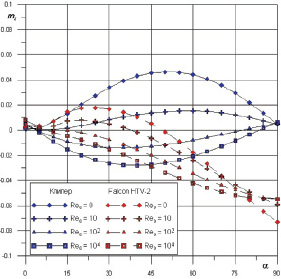
Рис. 4. Зависимость mz(a) для «Клипер» и «Falcon HTV-2»
Из этих результатов видно, что с увеличением числа Рейнольдса коэффициент сопротивления тела уменьшается (что можно объяснить уменьшением нормальных и касательных напряжений p1(Re0) и t0(Rе0)), при этом общий характер зависимости Cx(a) не изменяется. Зависимость Cy(a) является несимметричной при Re0 → ∞, так что значение Cy при положительных углах атаки существенно больше по модулю Cy при отрицательных углах атаки. Из этих результатов чувствительно, что коэффициенты силы сопротивления «Falcon HTV-2» меньше чем, «Клипера», и изменение числа Рейнольдса оказывает сильное влияние на все аэродинамические характеристики. Можно сказать, что число Рейнольдса влияет формы тела, и локальный метод дает хорошие результаты в переходном режиме для широкого класса тел.
Выводы
Проведен анализ различных подходов к расчету аэродинамических характеристик перспективных гиперзвуковых летательных аппаратов. Рассмотрен локальный метод для определения аэродинамических характеристик воздушно-космических систем. Представленные методики расчета имеют практический интерес для организаций и специалистов, занимающихся определением аэродинамических характеристик гиперзвукового летательного аппарата на конструкцию технических систем. Методики и результаты смогут быть полезны при создании современных и перспективных воздушно-космических аппаратов нового поколения.
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Рецензенты:
Боголепов В.В., д.ф.-м.н., главный научный сотрудник ФГУП «ЦАГИ», профессор МФТИ, г. Жуковский;
Липатов И.И., д.ф.-м.н., начальник отдела ФГУП «ЦАГИ», профессор МФТИ, г. Жуковский.
Работа поступила в редакцию 11.02.2014.



