Заготовки ковочных молотов при ударном деформировании проявляют упругие, пластические и вязкие свойства. При высоких уровнях нагружения, когда в заготовке возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации, т.е. заготовка проявляет пластические свойства.
Основная часть энергии удара молота расходуется на деформирование заготовки (работа деформации), часть энергии теряется на упругие деформации бойков, бабы, штока, стоек, станин, колебание шабота, фундамента и др. Заготовка в процессе деформирования поглощает механическую энергию (работу) в процессе ударной нагрузки, тем самым проявляя вязкие свойства.
Подавляющее большинство заготовок перед дальнейшей ковкой проходит операцию осадки, при которой в результате продольного удара увеличивается площадь поперечного сечения заготовки за счет уменьшения ее высоты.
Известен способ моделирования заготовки методом конечных элементов, реализуемый программным комплексом Аnsis. При использовании этого характеристики заготовки получаются случайным образом, вследствие чего не удается назначать вполне определенные технологические процессы ковки, исключающие брак.
Сущность предлагаемого подхода заключается в том, что заготовка моделируется в виде вязкоупругого тела Максвелла. Задача оценки осадки заготовки решается частотным методом, подробно описанным в работах [1, 2, 3, 4, 5].
Для вязко-упругого элемента Максвелла существуют следующие зависимости:
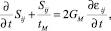
где tM – время релаксации напряжений; Sij – тензор напряжений; εij – тензор деформаций.
Вводя параметр преобразования Лапласа 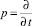 и учитывая, что при построении АФЧХ p = iω, получим:
и учитывая, что при построении АФЧХ p = iω, получим:
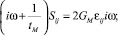
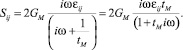
Откуда получаем выражения для характеристики E:
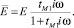
Коэффициент tM определяется экспериментальным путем.
Расчетная схема рассматриваемой задачи представлена на рис. 1.
Расчетной схеме (рис. 1) соответствует следующая система разрешающих уравнений:
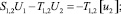
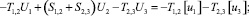
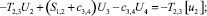 (1)
(1)
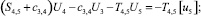
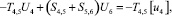
где
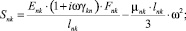
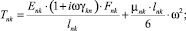
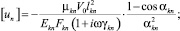
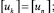
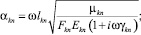
n, k – индексы, указывающие соответственно начало и конец участка; j – номер узла (i = 1,2…19); i – мнимая единица, 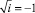 ; Еnk – модуль упругости участка nk, Па; Fnk – площадь поперечного сечения участка nk, м2; lnk – длина участка nk, м; mnk – масса единицы длины стержня участка nk, кг/м; V0 – скорость соударения с заготовкой, м/с; γnk – коэффициент сопротивления участка nk; ω – частота колебаний, с-1.
; Еnk – модуль упругости участка nk, Па; Fnk – площадь поперечного сечения участка nk, м2; lnk – длина участка nk, м; mnk – масса единицы длины стержня участка nk, кг/м; V0 – скорость соударения с заготовкой, м/с; γnk – коэффициент сопротивления участка nk; ω – частота колебаний, с-1.
Из системы разрешающих уравнений находятся изображения перемещений U(ω) в узлах системы. Для получения переходного процесса используется дискретное преобразование Фурье. Результат можно получить, осуществив численное интегрирование при t = 0…∞ по формуле
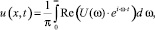 (2)
(2)
где u(x, t) – продольное перемещение поперечного сечения; х – координата сечения; t – время; ω – частота.
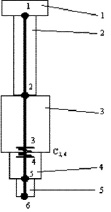
Рис. 1. Падающие части ковочного молота при ударе о заготовку: 1 – поршень; 2 – шток; 3 – баба; 4 – верхний боек; 5 – заготовка
Определение постоянных математической модели при ковке заготовки, взятой в виде тела Максвелла, производится следующим образом:
1. Производится экспериментальный удар молотом по разогретой заготовке.
2. Замеряется величина осадки заготовки.
3. Связь между постоянными тела Максвелла и осадкой заготовки находится по формуле (1), согласно которой строится переходный процесс.
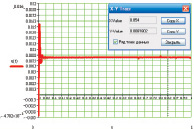
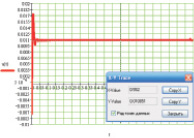
Построим кривые (рис. 2), заданные уравнениями (1, 2) при следующих исходных данных (табл. 1), взятых для ковочного молота модели М1345 и заготовок из табл. 2.
а 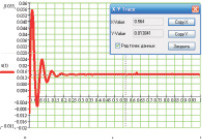 б
б 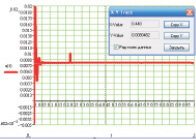
 г
г 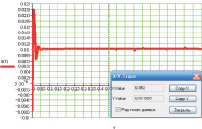
 е
е 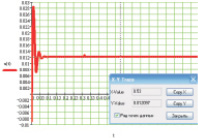
Рис. 2. Переходный процесс в точке контакта верхнего бойка с заготовкой ковочного молота: а, б, в, г, д, е – заготовки 1, 2, 3, 4, 5, 6 соответственно (табл. 2)
В результате численных расчетов, осуществленных с помощью программного комплекса MathCAD2001, получен переходный процесс в точке контакта верхнего бойка молота с заготовкой, представленный на рис. 2. Постоянные Максвелла подобраны так, чтобы расчетная осадка заготовки согласовывалась с данными экспериментальных исследований (табл. 3).
Предлагаемый подход теоретического расчета осадки заготовки имеет ценность, заключающуюся в возможности предварительной оценки ее прочности. Возможность теоретического расчета напряжений и деформаций, возникающих в деталях ковочного молота и заготовки, позволяет назначать оптимальные технологические режимы ковки.
Таблица 1
Исходные данные для расчетов
|
Начало участка |
Конец участка |
l, м |
Е, Па |
F, м2 |
ρ, кг/м3 |
|
1 |
2 |
1,6 |
2,1∙1011 |
0,024 |
7800 |
|
2 |
3 |
0,906 |
2,1∙1011 |
0,39 |
7800 |
|
3 |
4 |
пружина с жесткостью 75×106 кг/м |
|||
|
4 |
5 |
0,3 |
2,1∙1011 |
0,204 |
7800 |
|
5 |
6 |
0,115 |
7∙109 |
0,0016 |
7620 |
Таблица 2
Результаты экспериментальных исследований
|
№ п/п |
Материал заготовки |
Температура ковки, °С |
Форма и размеры заготовки, мм |
Расстояние от заготовки до верхнего бойка до удара, мм |
Величина отскока, мм |
Размеры заготовки после удара, мм |
Осадка заготовки, мм |
|
1 |
АК6 |
470 |
∅50×90 |
860 |
20 |
∅54×75 |
15 |
|
2 |
АК6 |
470 |
∅250×327 |
623 |
150 |
∅254×317 |
10 |
|
3 |
12Х18Н10Т |
1180 |
∅105×137 |
813 |
18 |
∅108×130 |
7 |
|
4 |
30ХГСА |
1180 |
∅50×70 |
880 |
20 |
∅54×60 |
10 |
|
5 |
ВТ-22 |
950 |
∅170×272 |
678 |
20 |
∅174×260 |
12 |
|
6 |
ВТ-6 |
980 |
∅70×120 |
830 |
50 |
∅73×110 |
10 |
Таблица 3
Результаты определения постоянных математической модели
|
№ п/п |
Материал заготовки |
Экспериментальная осадка заготовки, мм |
Расчетная осадка заготовки согласно формуле (1) |
Расхождение, % |
Экспериментальный коэффициент tM |
|
1 |
АК6 |
15 |
13,8 |
8 |
0,002 |
|
2 |
АК6 |
10 |
8 |
20 |
0,005 |
|
3 |
12Х18Н10Т |
7 |
8,1 |
16 |
0,003 |
|
4 |
30ХГСА |
10 |
11,1 |
11 |
0,005 |
|
5 |
ВТ-22 |
12 |
10,8 |
10 |
0,003 |
|
6 |
ВТ-6 |
10 |
12,1 |
21 |
0,007 |
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск;
Антонец И.В., д.т.н., профессор Ульяновского государственного технического университета, г. Ульяновск.
Работа поступила в редакцию 27.01.2014.



