Задача прогнозирования состояния организма человека относится к классу плохо формализуемых задач, поскольку речь идет о сложной и нерешенной в настоящее время задаче определения границы между здоровьем и болезнью. На практике для решения плохо формализуемых задач часто привлекают аппарат, обеспечивающий изучение структуры данных с выдвижением соответствующих гипотез на языке специалистов исследуемой предметной области. В анализе данных таким аппаратом является вычислительный эксперимент. Для решения задач классификации вычислительный эксперимент реализуется с помощью диалоговых интерактивных систем распознавания образов (ДСР) [1, 2].
Для привлечения ДСР к решению задач прогнозирования рассмотрим такой ее двухальтернативный вариант: класс ω0 – обследуемый в течение заданного времени Т0 не переходит в состояние болезни с именем ℓ (не переходит в класс ωℓ); класс ωℓ – обследуемый в течение времени Т0 переходит в состояние ωℓ. Таким образом, задача прогнозирования превращается в задачу классификации двух состояний ω0 и ωℓ, которая имеет ряд особенностей, значительно осложняющих соответствующую задачу обучения в терминологии распознавания образов. Основными из этих особенностей являются: отсутствие полного статистического материала, одновременно охватывающего различные стороны функционирования исследуемого объекта; наличие казуистических ситуаций; присутствие в обучающем материале объектов с неточными или ошибочными описаниями; часто «учитель» не имеет возможности точно указать класс объекта на обучающей выборке и не дает информации о наличии переходных зон между классами, хотя в обучающей выборке эти объекты имеются; объекты одного и того же класса в исходном пространстве могут быть представлены различными группами, которые, в свою очередь, распределены среди групп других классов и т.д. [1, 2, 4, 5].
Для разрешения этих и ряда других проблем, связанных с особенностями задач медицинского прогнозирования, в данной работе предлагается использовать модификацию известных ДСР, определенную в работах [2, 4] как метод интерактивного конструирования двумерных классификационных пространств (ИКДКП), который способен сохранять работоспособность при плохо формализованной структуре классов с нарушениями гипотезы о компактности, при большом количестве артефактов в обучающей выборке, в условиях не полностью определенных «учителем» классов, возможной «вложенности» их друг в друга и др. [2].
Основная идея предлагаемого метода заключается в том, что обучение и классификация ведутся в двумерном отображающем пространстве Φ = Y1×Y2, куда многомерные объекты X = (x1, x2, ..., xn) отображаются с помощью пары отображающих функций Y1 = φ1(A, X), Y2 = φ2(B, X), где A = (a1, a2, ..., an) и B = (b1, b2, ..., bn) – векторы настраиваемых параметров. Задача обучения состоит в нахождении таких значений параметров векторов А и В и видов функциональных зависимостей φ1 и φ2, при которых непересекающиеся образы в многомерном пространстве N при отображении в Ф будут разделимы или будут иметь минимальное (допустимое) наложение классов ω0 и ωℓ. С математической точки зрения задача обучения заключается в минимизации функционала качества вида:
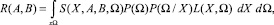(1)
где P(Ω) – априорная вероятность появления класса Ω; P(Ω/X) – условная вероятность появления Ω; L(X, Ω) – функция потерь от ошибочной классификации, например, из-за недостаточной классификации «учителя»; S(X, A, B, Ω) – площадь наложения классов в Ф.
Задача классификации заключается в определении местоположения отображения объектов X = (x1, ..., xn) относительно границ различных классов, полученных в Ф.
В качестве функций отображения могут применяться как простейшие линейные формы, так и нелинейные модели.
Известно несколько способов динамического конструирования отображающего пространства. Например, один из его вариантов основан на том, что в исходном пространстве признаков выбирается эталонная структура и создается механизм ее скольжения по некоторой средней (в смысле выбранного критерия усреднения) линии, представляющей каждый из исследуемых классов. Получающуюся в результате такого скольжения линию называют «скелетной», поскольку она является основой, вокруг которой формируется вся гиперконфигурация класса, подобно тому, как вокруг скелета формируется конфигурация тела [3].
В практических приложениях исследуемые классы состояний ω0 и ωℓ достаточно сильно пересекаются и имеют размытые границы в исходном пространстве признаков, что, естественно, передается и в отображающее пространство. В таком варианте целесообразно использовать нечеткое описание отображений классов с выделением соответствующих областей уверенности в классификации, коэффициентов уверенности и (или) функций принадлежности [2, 3, 5].
Для изображения в Ф зон с различной уверенностью в классификации удобно использовать линии равных значений коэффициентов уверенности (значений функций принадлежности) или соответствующие цветовые гаммы. Для отображающего пространства Ф функция принадлежности к классу ωℓ может быть определена на базовой переменной, соответствующей расстоянию dk от отображения исследуемого объекта с координатами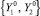 
до опорных конфигураций Lk класса ωℓ.
В качестве опорных конфигураций в зависимости от целей и типов решаемых задач могут быть выбраны координаты центра отображений классов, опорные точки с координатами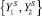 
внутри или вне классов, скелетные (усредняющие) линии классов (прямые линии с уравнениями типа a1Y1 + a2Y2 + a0 = 0, ломаные линии), эталоны различных конфигураций (круги, квадраты, прямоугольники), собственно границы классов, которые в общем случае описываются уравнениями вида fk(A, Y1, Y2) = 0.
На этапе обучения специальная компьютерная программа или группа экспертов определяет семейство функций принадлежности μℓ(dk). Далее уверенность в принятии решения определяется по отношению к ближайшей Lk.
Например, если границы классов в пространстве Ф определяются кусочно-линейной аппроксимацией, то до каждой из k линий базовая переменная dk определяется выражением
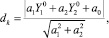(2)
а общая уверенность (коэффициент уверенности) в классификации ωℓ определяется выражением
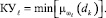(3)
В качестве практического примера рассмотрим решение задачи синтеза решающего правила для прогнозирования послеоперационных осложнений после трансуретральной резекции предстательной железы класс ωR [5].
Для получения прогностических решающих правил было отобрано 12 медицинских признаков для построения соответствующих математических моделей: x1 – наличие в анамнезе острой задержки мочеиспускания, катетеризации мочевого пузыря; x2 – наличие эпицистостомы; x3 – степень инфицирования мочи (КОЕ/мл); x4 – количество лейкоцитов в поле зрения; x5 – наличие сопутствующих воспалительных заболеваний мочевыделительной системы; x6 – суммарный балл оценки симптомов (I – PSS); x7 – качество жизни вследствие расстройств мочеиспускания (L); x8 – состояние иммунитета по показателю CD 8; x9 – показатель иммунитета по интерлейкину – 4; x10 – показатель иммунитета по тесту восстановления нитросинеготетразолия (НСТ – тест); x11 – антиокислительная активность (АОА) сыворотки крови (в %); x12 – количество церулоплазмина в сыворотке крови.
В ходе проведения разведочного анализа с использованием пакета прикладных программ, описанного в работах [2, 4], было установлено, что при разделении классов ω0 и ωR наибольшей информативностью обладают признаки x4, x6, x11 и x12, причем пара признаков x4 и x6 оперативно и легко получается в ходе обследования. На объектах репрезентативной обучающей выборки в системах координат {x4, x6} были построены образы классов: ω0 – осложнений не ожидается; и ωR – ожидаются послеоперационные осложнения (рис. 1).
Таким образом, отображающее пространство Ф в данном варианте построено на координатах исходного пространства признаков: Y1 = x6; Y2 = x4.
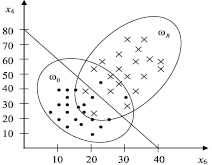
Рис. 1. Расположение классов ω0(x) и ωR(x) в двумерном пространстве признаков
Анализ изображений полученных образов показал, что между классами ω0 и ωR может быть проведена разделяющая линия типа x4 + 2x6 = 80 с выделением зоны пересечений этих классов.
Рассматривая зону пересечения как область нечеткой классификации и используя переменную Z = x4 + 2x6 в качестве базовой переменной, была построена пара функций принадлежности к классам ω0 и ωR (рис. 2).
Максимальное значение функций принадлежности на уровне 0,92 определяет доверие экспертов к полученному решающему правилу. Решение о прогнозировании принимается по максимальной величине соответствующих функций принадлежности.
Предложенный метод классификации обеспечивает хорошие результаты и при решении задач ранней и дифференциальной диагностики различных заболеваний. В качестве второго примера рассмотрим задачу нечеткой классификации вибрационной болезни по трем классам: здоров (ω0); ранняя (доклиническая, донозологическая) стадия (класс ωp); клиническая стадия (класс ωk) вибрационной болезни.
Для решения классификационной задачи было выбрано 24 признака xi: х1 – профстаж работы с инструментом не менее 8 лет; х2 – парастезия рук после работы и ночью; х3 – боли в руках после работы и ночью; х4 – зябкость рук; х5 – тугоподвижность пальцев рук по утрам; х6 – судорожные стягивания пальцев рук; х7 – прерывистость сна из-за болей и парастезий в руках; х8 – побеление или посинение пальцев; х9 – гиперемированный акроцианоз с мраморностью; х10 – акрогипотермия; х11 – акрогипергидроз; х12 – трофическое изменение кистей; х13 – гипалгезия (гипреалгезия) по типу «перчаток»; х14 – снижение вибрационной чувствительности; х15 – спастический или спастикоатонический тип капилляров; х16 – термоассиметрия на кистях и груди более 0,5 °С; х17 – акрационаз при холодной пробе; х18 – акроспазмы (синдром Рейно); х19 – замедленное восстановление кожной температуры после холодовой пробы; х20 – снижение силы рук; х21 – преобладание периферических сосудистых нарушений над церебральными по данным РЭГ, ПРГ; х22 – костные нарушения кистей и позвоночника; х23 – наличие неврита лучевого, локтевого нерва; х24 – хроническая коронарная недостаточность.
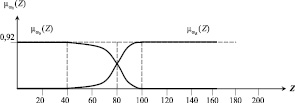
Рис. 2. Графики функций принадлежностей к классам ω0 и ωR
В ходе обучения была получена пара отображающих функций вида:
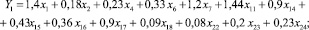
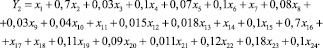
Относительно выделенных экспертами границ классов в пространстве Ф согласно рекомендациям [1, 3] получены функции принадлежности, графики которых приведены на рис. 3.
а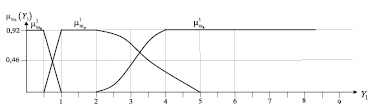
б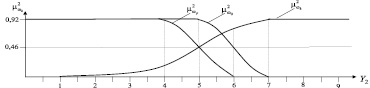
Рис. 3. Графики функций принадлежности к классам вибрационной болезни по шкале: а – Y1; б – Y2
Решение о принадлежности к каждому из классов ωℓ (ℓ = 0, p, k) принимаются в соответствии с выражениями
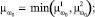
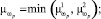
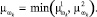
Решение о классификации принимается по максимальной величине функций принадлежности. При равных значениях функций принадлежности предпочтения отдаются в следующем порядке ωk, ωp, ω0, начиная с ωk.
Проверка качества классификации на контрольной выборке объемом 50 человек на каждый класс показала, что полученная диагностическая эффективность решающих правил превышает 0,9, что позволяет рекомендовать их к использованию в медицинской практике.
Аналогичные результаты были получены в задаче диагностики профессиональных заболеваний сварщиков с уверенностью в дифференциальной диагностике таких заболеваний, как интоксикация, пневмокониоз и хронический бронхит на уровне 0,9 при диагностической эффективности не ниже 0,88.
Выводы
Рассматриваемый метод интерактивного конструирования двумерных классификационных пространств позволяет решать задачи прогнозирования, ранней и дифференциальной диагностики заболеваний в условиях плохой формализации, недостаточной статистики, различной структуры классов и признакового описания, при наличии казуистических ситуаций, отсутствии информации об объективно существующих переходных зонах между классами и отсутствии априорной информации о структуре классов. Кроме того, разработанные методы позволяют изучать структурные особенности исследуемых классов, получать дополнительные сведения как о структуре классов, так и о системе признаков, представляющих эти классы, включая выяснение роли признаков в формировании того или иного класса или зоны перехода между классами.
Практическая апробация метода интерактивного конструирования двумерных классификационных пространств показывает приемлемые для практической медицины результаты по качеству классификации.
Рецензенты:
Мишустин В.Н., д.м.н., профессор, декан факультета последипломного образования, ГОУ ВПО «Курский государственный медицинский университет» Росздрава, г. Курск;
Бурмака А.А., д.т.н., профессор, главный научный сотрудник НИЦФГУП 18 ЦНИИ МО РФ, г. Курск.
Работа поступила в редакцию 27.01.2014.