Теория катастроф как раздел математики начала формироваться еще в середине ХХ века на основе теории особенностей гладких отображений, заложенной математиком Хасслером Уитни, и теории бифуркаций динамических систем А. Пуанкаре и А.А. Андронова. Теория особенностей представляет собой обобщение исследования функций на максимум и минимум, при этом в теории Уитни [11] функции заменены отображениями – наборами нескольких функций нескольких переменных. Теория бифуркаций (раздвоений) изучает качественные перестройки различных объектов при изменении параметров, от которых они зависят. Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий [1].
Создателями теории катастроф являются французский математик Р. Том [10] и российский математик В.И. Арнольд [1]. Большой вклад в ее развитие внесли Т. Постон, И. Стюарт [4], Дж.М.Т. Томпсон [6], Р. Гилмор [7, 8], К. Зиман [12].
Среди семи элементарных катастроф большое значение имеет катастрофа сборки, потенциальная функция которой определяется
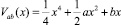, (1)
и многообразие M катастрофы задается уравнением
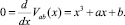(2)
Рис. 1 иллюстрирует поведение поверхности равновесия (или многообразие катастрофы) с ее проекцией на плоскость ab, определяющую управляющие параметры a и b.
Точка (a,b), медленно изменяя свои координаты a и b, описывает некоторую траекторию на плоскости ab. Тогда наблюдаемое положение равновесия пройдет путь на поверхности M, лежащий над путем в плоскости ab. Из-за сборки на поверхности равновесия M этому пути, возможно, придется перескакивать с одного листа поверхности на другой. Это объясняется тем, что точки многообразия M, расположенные на внутренней поверхности складки, соответствуют неустойчивому состоянию системы. Такой очень быстрый скачок системы (катастрофа) наступает только при выходе из области I, так как у системы не остается другого выбора (принцип максимального промедления (perfect delay) Р. Тома [10]). Таким образом, гладкие изменения переменных управления a и b могут повлечь за собой разрывные изменения переменной состояния x, вызывая катастрофические прыжки.
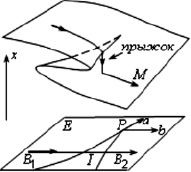
Рис. 1. Катастрофа сборки
Кубическое уравнение (2) имеет от одного до трех вещественных корней. Природа этих корней зависит от дискриминанта
D = 4a3 + 27b2. (3)
Пространство управляющих параметров, образующих плоскость ab, разбивается на пять подмножеств: B1, B2, P, I, E, изображенных на рис. 2. Линия, образуемая множествами B1, B2, и P, соответствует условию D = 0, т.е. 4a3 + 27b2 = 0.
При этом, если a ≠ 0 и b ≠ 0, то точка (a, b) лежит в B1 или в B2, и уравнение (2) имеет три вещественных корня, два из которых совпадают между собой. Точка P соответствует a = b = 0 и имеются три совпадающих вещественных корня, равных нулю. Точка P называется точкой возврата.
Если (a, b) ∈ I, то имеется три различных вещественных корня и D < 0.
Если (a, b) ∈ E, то имеются только один вещественный корень (D > 0).
Катастрофа происходит, когда траектория точки (a, b) покидает область I и при этом D меняет знак с отрицательного на положительный.
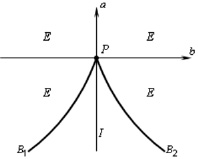
Рис. 2. Пространство управляющих параметров
Полагаем, что изменения управляющих параметров являются случайными. Случайными величинами или случайными функциями можно описывать нагрузку, размеры элементов конструкций вследствие их рассеяния в пределах полей допусков, механические свойства материалов и т.д. Для практических целей важен статистический анализ положений равновесия вблизи критических точек. Поэтому представляется целесообразным рассмотреть с позиций теории катастроф вопросы оценки показателей надежности при наличии случайных возмущающих факторов.
Рассмотрим катастрофу сборки (1) со стохастических позиций. Переменные управления a и b в общем случае изменяются во времени, и характеристика состояния будет определяться случайным процессом D(t). Таким образом, необходимо решать задачу о выбросах случайного процесса из области I. При этом вероятность возникновения катастрофы
P(t) = P{D(t) > 0}.
Пусть D(t) – дифференцируемый случайный процесс,
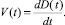
Нас интересует вероятность того, что реализация случайного процесса D(t) пересечет нулевой уровень (рис. 3). Для того чтобы выброс произошел, необходимо осуществление двух событий:
1) в момент времени t, предшествующий выбросу, ордината D(t) должна быть меньше нуля (D(t) < 0);
2) в момент времени t + dt, следующий за моментом t (в тот момент, когда произойдет выброс) ордината случайной функции должна быть положительной, т.е. D(t + dt) > 0.
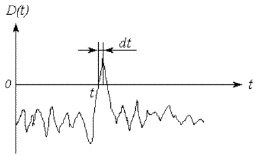
Рис. 3. Реализация случайного процесса D(t)
Таким образом, вероятность того, что выброс произойдет в бесконечно малом интервале времени (t, t + dt) [9]
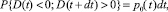(4)
где p0(t) – временная плотность вероятности.
Выразим в выражении (4) D(t + dt) через D(t). Для этого разложим D(t + dt) в ряд Тейлора в окрестности точки t
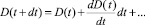
Отсюда
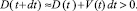
После переноса V(t)dt в правую часть неравенства получим
D(t) > 0 – V(t)dt.
С учетом зависимости (4)
– V(t)dt < D(t) < 0.
вероятность выброса запишется в виде
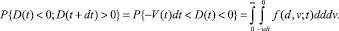
Здесь f(d, v; t) – двумерный закон распределения ординат D и скоростей V.
После применения теоремы о среднем
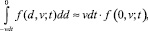
получим
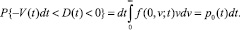
Здесь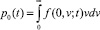 
– временная плотность для вероятности выброса.
Временную плотность p0(t) можно трактовать как среднее число пересечений случайным процессом D(t) нулевого уровня в единицу времени.
В общем случае среднее число пересечений уровня 0 за время τ (математическое ожидание числа выбросов)
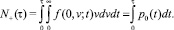(5)
Для стационарного процесса плотность распределения ординат и скоростей не зависит от времени, т.е. f(d, v; t) = f(d, v) и, следовательно, p0(t) = p0. Отсюда
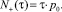(6)
Во многих задачах практический интерес представляет вариант, при котором среднее число выбросов за данный промежуток времени достаточно мало и можно считать появления последовательных выбросов независимыми «редкими» событиями. В этом случае число появлений выбросов можно считать приближенно подчиняющимся закону распределения Пуассона [5], при этом единственным параметром, входящим в закон распределения, является математическое ожидание числа выбросов, определяемое формулами (5) или (6). Тогда в общем случае вероятность безотказной работы определится
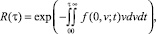(7)
для стационарного процесса
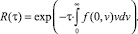(8)
Имеет место и другой подход, изложенный в работах А.В. Питухина [2, 3]. При этом для оценки вероятности катастрофы сборки предложены аналитический метод и метод статистической линеаризации для варианта, когда управляющие параметры a и b являются случайными величинами. Воспользуемся методом статистической линеаризации для оценки математического ожидания и дисперсии случайного процесса D(t) в случае, когда переменные управления являются стационарными случайными функциями (процессами). Исходя из формулы (3), получим
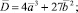(9)
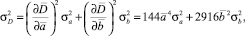(10)
где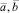 
– математические ожидания стационарных случайных процессов a(t) и b(t); 
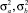– дисперсии стационарных случайных процессов a(t) и b(t).
Имея значения оценок (9) и (10) и полагая вид закона распределения дискриминанта D известным, применяя метод моментов Пирсона, можно определить неизвестные значения параметров θ1, θ2 предполагаемого распределения F(d, θ1, θ2).
Тогда вероятность безотказной работы определится
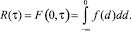(11)
Вероятность отказа (вероятность катастрофы сборки)
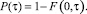(12)
Предложенные подходы позволяют произвести статистический анализ положений равновесия вблизи критических точек, что важно для практических целей. Полученные зависимости могут быть применены для оценки вероятности безотказной работы различных элементов конструкций машин и оборудования с позиций теории катастроф.
Работа выполнена при поддержке Программы стратегического развития (ПСР) Петрозаводского государственного университета в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.
Рецензенты:
Григорьев И.В., д.т.н., профессор кафедры технологии лесозаготовительных производств Санкт-Петербургского государственного лесотехнического университета, г. Санкт-Петербург;
Заика Ю.В., д.ф.-м.н., профессор, заведующий лабораторией моделирования природно-технических систем, Институт прикладных математических исследований Карельского научного цента РАН, г. Петрозаводск.
Работа поступила в редакцию 27.01.2014.