Сцепляющее (или диспергирующее) усилие в аппаратах с магнитоожиженным слоем ферротел (электромагнитных механоактиваторах, приборах контроля загрязненности технологических сред ферропримесями, электромагнитных мешалках и т.д.) [1, …, 6] создается с использованием двух потоков энергии: энергии постоянного по знаку и регулируемого по величине электромагнитного поля, а также энергии, поступающей от приводного электродвигателя. Использование двух потоков энергии позволяет осуществлять тонкое и надежное управление величиной силовых взаимодействий между ферромагнитными рабочими элементами в процессе их переориентации в структурных группах [7, 8, 9]. Множество факторов, которыми в магнитоожиженном слое ферротел можно воздействовать на продукт в нужном направлении, требует, прежде всего, знания физической сущности происходящих в рабочих объемах явлений и их основных закономерностей.
Цель работы ‒ исследование эффективности работы аппаратов с магнитоожиженным слоем на основании анализа динамики рабочего процесса деформации и разрушения структурной группы из ферромагнитных элементов сферической формы при формировании сцепляющего (или диспергирующего) усилия.
Материалs и методы исследований
Предметом исследований являются физико-механические процессы в магнитоожиженном слое феррочастиц сферической формы при формировании сцепляющего (или диспергирующего) усилия.
Результаты исследования и их обсуждение
При рассмотрении задачи о движении цепочки из металлических шаров в радиальном магнитном поле рабочих объемов аппаратов с магнитоожиженным слоем различного целевого назначения [1, …, 6] принимаем во внимание, что диаметр внутреннего вращающегося электрода R велик по сравнению с диаметром R0 размольных шаров. Эту задачу в первом приближении можно заменить задачей о движении структурной группы шаров в однородном поле (рис. 1). Ошибка от такой замены имеет порядок 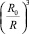 .
.
Для описания движения цепочки шаров примем следующие обобщенные координаты: x – абсцисса центра 0-го шара; φ0 – угол поворота 0-го шара; νi – угол, который составляет линия, соединяющая центры i – 1 и i-го шаров с осью ординат; φi – угол поворота i – шара.
В задаче рассматривается n + 1 число шаров, причем, i-й и i + 1 (i = 0,…, n) касаются друг друга.
Условием разрыва цепочки шаров является достижение какого-либо угла ν значения ±νкр, которое определяется формулой [7, 9]
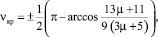 (1)
(1)
где μ – магнитная проницаемость размольных шаров.
В этот момент сила давления между шарами обращается в ноль.
Момент инерции шара относительно оси, проходящей через его центр, равен:
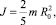 (2)
(2)
где m – масса шара.
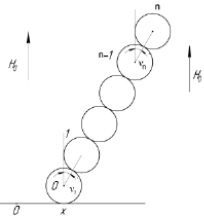
Рис. 1. Схема движения структурных групп из ферромагнитных шаров в однородном магнитном поле
Из рис. 1 следует, что координаты к-го шара определяются уравнениями
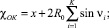
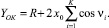 (3)
(3)
Скорость центра к-го шара νок с учетом уравнений (3) описывается следующим выражением:
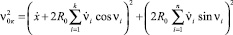
или
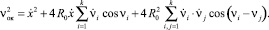 (4)
(4)
Таким образом, кинетическая энергия системы из к шаров определяется следующей рекурентной формулой:
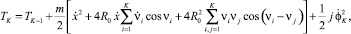 (5)
(5)
где ТК-1 – кинетическая энергия системы K – 1 шаров.
Для шара, расположенного в основании структурной группы, т.е. у поверхности стенки рабочего объема, кинетическая энергия Т0 равна:
 (6)
(6)
Для рассматриваемой системы выражение для элементарной работы δАК имеет вид:
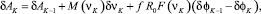 (7)
(7)
где δАК-1 – элементарная работа системы шаров к – 1; М(νк) и F(νк) – соответственно силы и момент сил взаимодействия однородного магнитного поля с системой шаров. Их значения определяются формулами 8 и 9 соответственно:
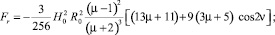 (8)
(8)
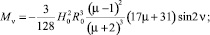 (9)
(9)
f – коэффициент трения 0-го шара о стенку рабочего объема;
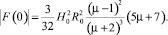
Для составления уравнений движения структурной группы из феррошаров в рабочем объеме ЭММА воспользуемся уравнениями Лагранжа второго рода:
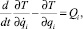 (10)
(10)
где qi – обобщенные координаты; Qi – обобщенные силы.
Анализ уравнения Лагранжа второго рода для рассматриваемой задачи показывает, что уравнения распадаются на две группы. К первой группе относятся уравнения, в которые входят только переменные x, νi и их производные, а во вторую группу все остальные уравнения. Для решения поставленной задачи интерес представляют только уравнения первой группы. Эти уравнения можно получить, если в выражениях для кинетической энергии (5) и элементарной работы (6) и (7) положить все φi = 0.
Итак, рассмотрим цепочку, состоящую из двух шаров в однородном магнитном поле, и составим дифференциальные уравнения движения этой цепочки.
Для рассматриваемого случая из уравнений (5) и (7) получим:
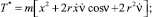 (11)
(11)
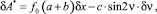 (12)
(12)
где
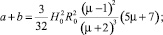
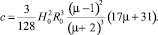
Тогда уравнения Лагранжа второго рода примут следующий вид:
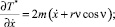
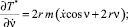
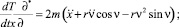
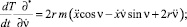
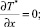
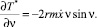
Отсюда дифференциальные уравнения движения цепочки определяются выражениями
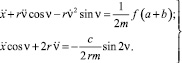 (13)
(13)
Исключая из уравнения (13)  , получим:
, получим:
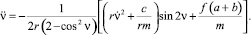 (14)
(14)
Уравнение (14) можно представить в виде следующей системы:
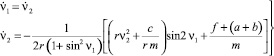 (15)
(15)
с начальными условиями v1(0) = 0 и v2(0) = 0.
Численное интегрирование системы (15) осуществлялось с использованием ПК с помощью метода Runge-cutt с постоянным выбором шага интегрирования. Из всего многообразия полученных данных для различных сочетаний входных параметров наибольший интерес представляют результаты, представленные на рис. 2.
Установлено, что решающее значение на процесс разрушения структурной комбинации из ферротел сферической формы оказывает параметр f = f0 (здесь f0 – коэффициент трения 0-го шара о стенку рабочей емкости).
При значениях f0 ˂ 0,8 линии, описывающие изменение угла деформации ν цепочки и критического угла ее наклона νкр, при котором сила взаимодействия между шарами равна 0, не пересекаются. То есть для данных условий деформации не достигается равенство ν = νкр, и цепочка из ферротел не подвергается разрушению. Визуальными наблюдениями на макетах аппаратов с магнитоожиженным слоем (с открытыми для наблюдений рабочими объемами) установлено, что «слой скольжения» в рассматриваемых случаях смещается в основания структурных построений и организуется между стенками рабочей емкости и смежными с ними шарами структуры.

Рис. 2. Анализ деформации и разрушения структурной группы из ферромагнитных размольных элементов сферической формы в рабочем объеме аппаратов с магнитоожиженным слоем: 1 – f0 ˂ 0,8; 2 – f0 = 0,8; 3 – f0 > 0,8
Представленные на рис. 2 данные свидетельствуют, что при f ≥ 1 угол ν в процессе деформирования цепочки достигает своего критического значения ν = νкр, что обусловливает ее разрушение. Причем более динамичное разрушение осуществляется при больших значениях коэффициента трения между шарами, расположенными в основании структуры, со стенками рабочего объема исследуемых аппаратов с магнитоожиженным слоем.
Заключение
В результате исследований движения мелющих тел в постоянном по знаку электромагнитном поле при относительном смещении поверхностей рабочего объема получена математическая модель, описывающая динамику рабочего процесса формирования сцепляющего (или диспергирующего) усилия. На основании анализа решений дифференциальных уравнений Лагранжа II рода, составленных с учетом физических аспектов создания силовых контактов в слое ферротел, определены принципы конструктивного исполнения аппаратов. Из изложенного следует, что одним из основных условий эффективной работы аппаратов с магнитоожиженным слоем является создание устойчивых оснований структурных построений из феррочастиц. Это достигается за счет увеличения коэффициента трения f0 между внутренним электродом аппаратов и феррочастицами в основании структурных построений. Устройство ребер, рифлений и т.д. на смещающихся друг относительно друга поверхностях рабочего объема [2] обеспечивает жесткое сцепление оснований структурных групп с этими поверхностями и способствует организации «слоя скольжения» в средней части рабочего объема. Целенаправленная и регулируемая переориентация ферроэлементов в средней части магнитоожиженного слоя с образованием «слоя скольжения» обеспечивает заданные условиями производства силовые и энергетические условия проведения технологических процессов [3, 4, 9, 10].
Рецензенты:
Карпов В.Н., д.т.н., профессор Института технических систем, сервиса и энергетики, заслуженный деятель науки и образования России, г. Санкт-Петербург;
Ракутько С.А., д.т.н., профессор, заведующий лабораторией энергоэффективных электротехнологий, ГНУ СЗ НИИМЭСХ, г. Санкт-Петербург.
Работа поступила в редакцию 21.01.2014.



