Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Выявление взаимосвязей между малыми телами Солнечной системы представляет несомненный интерес, так как позволяет решать вопросы их происхождения и эволюции. Уже в 1876 г. Д. Кирквуд выявил 10 групп астероидов, двигавшихся по сходным орбитам и состоявших из 2–3 астероидов [6]. По его мнению, эти астероиды можно было рассматривать как осколки более крупных тел. К 1899 г. среди 417 астероидов было выявлено 20 пар с близкими орбитами. Однако, по мнению Хираямы [13], сходство орбит еще не означает общность их происхождения. Такое сходство могло быть и случайным, образовавшимся под действием различных факторов. С другой стороны, даже если астероиды и имеют общее происхождение и на начальном этапе элементы их орбит близки между собой, то под действием планетных возмущений орбиты могли очень сильно измениться. Хираяма поставил вопрос: можно ли выявить семейства астероидов, образовавшиеся в далеком прошлом?

Для решения этой задачи Хираяма использовал так называемые собственные элементы орбит, которые слабо изменяются под действием планетных возмущений. Исследуя собственные наклоны и эксцентриситеты, он выявил пять семейств астероидов в главном поясе, в которые вошли десятки известных астероидов.

Для выявления семейств довольно часто применяется критерий Тиссерана – T, который вычисляется по формуле

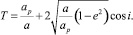(1)

В формуле (1) ap – большая полуось орбиты возмущающей планеты, а – большая полуось орбиты астероида, e – ее эксцентрисистет, а i – наклон.

Критерий Тиссерана использовался, например, в работе [15] для поиска возможных семейств среди коротко-периодических комет и околоземных астероидов.

Рассматривая только вековые возмущения, в работах [2–3] были получены две константы C1 и C2 (постоянные Лидова), которые вычислялись по формулам

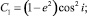
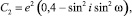(2)

где ω – аргумент перигелия орбиты астероида. Постоянство C1 вытекает из критерия Тиссерана, если учесть, что большие полуоси не содержат вековых возмущений. C2 также слабо изменяется под действием вековых возмущений и вместе с C1 описывает синхронные изменения эксцентриситета, наклона и аргумента перигелия. При ω = 0 или 180° наклон достигает максимума, а эксцентриситет – минимума, при ω = 90° или 270° наклон минимальный, а эксцентриситет – максимальный.

Для выявления близких орбит на текущий момент времени для последующего изучения возможности их взаимосвязи разработан ряд критериев [11, 14, 16]. Исторически первым является D-критерий Саутворта и Хокинса [18]. Считается, что этот критерий является метрикой в пятимерном нелинейном пространстве элементов орбит. Значение критерия вычисляется по формуле

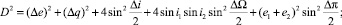(3)

где

Δe = e1– e2; Δi = i1 – i2; Δq = q1 – q2; ΔΩ = Ω1 – Ω2; Δπ = π1 – π2, (4)

а e1, e2, i1, i2, q1, q2, Ω1, Ω2, π1, π2 – эксцентриситеты, наклоны, перигелийные расстояния, долготы восходящих узлов и долготы перигелиев двух сравниваемых орбит соответственно. Отметим, что неявно этот критерий использует условие пересечения орбит исследуемых объектов с орбитой Земли, в одном из узлов, и по этой причине является метрикой в четырехмерном пространстве.

Предельное значение D-критерия – DС, оценивается по формуле [14]

DС = 0,20(360/N)1/4, (5)

в которой N – объем базы данных.

Отметим, что поиск семейств малых тел в Солнечной системе ведется непрерывно [4–5, 11–16, 19]. Наиболее актуальным направлением, по нашему мнению, является выявление семейств среди астероидов групп Аполлона и Атона [17].

Астероид 2004MN4 был открыт 19 июня 2004 г. в обсерватории Китт Пик (США) [10]. В 2004 г. были выполнены первые расчеты эволюции его орбиты и предсказана возможность столкновения этого астероида с Землей в 2029 г. В 2005 г. астероиду было присвоено имя египетского бога – Апофис и порядковый номер 99942.

Дополнительные наблюдения и более точные вычисления планетных возмущений выявили высокую вероятность его столкновения с Землей в 2036 г. Поэтому астероид Апофис (99942) был классифицирован как потенциально опасный для Земли. Размер Апофиса оценивается примерно в 270 м, масса – 2,7 1010 кг, а скорость его столкновения с Землей составит 12,59 км/с [8]. По различным оценкам, энергия, выделяющаяся при таком столкновении, будет эквивалентна 500–800 Мт в тротиловом эквиваленте. Последствия такой катастрофы могут быть губительны для жизни на Земле.

Астероид Апофис, с периодом обращения вокруг Солнца менее года, является часто наблюдаемым объектом. На данный момент известно более 1525 наблюдений, выполненных с 2004 по 2012 гг. Новые астрометрические данные используются для повышения точности орбиты и, следовательно, помогут уточнить вероятность столкновений. Так как большая полуось орбиты Апофиса a < 1 a.e., а афелийное расстояние Q > 1 a.e., то он был классифицирован как астероид группы Атона [17].

Элементы орбиты Апофиса приведены в табл. 1 согласно [8]. В ней даны: большая полуось – a, эксцентриситет – e, перигелийное расстояние – q, афелийное расстояние – Q, наклон – i, долгота восходящего узла – Ω, аргумент перигелия – ω и долгота перигелия – π = ω + Ω.

Таблица 1

Элементы орбиты Апофиса на эпоху 30,0 сентября 2012 г. (равноденствие 2000.0) по данным Jet Propulsion Laboratory (США)

Вторжения астероидов и комет в атмосферу Земли, а также твердых продуктов их разрушения происходят со скоростями от 11,2 до 72 км/с и порождает болидные и/или метеорные явления. Поиск болидов, возможно связанных с Апофисом [1], дал положительный результат – было обнаружено 4 таких болида. Следовательно, можно сделать вывод, что возраст Апофиса достаточно велик и в прошлом Апофис, или его родительское тело подверглось разрушению в результате столкновения с другим астероидом (астероидами). В результате таких столкновений с его поверхности могли быть выбиты фрагменты самых разных размеров. Возможно, что и сам Апофис является результатом дробления более крупного астероида. При этом могли образоваться не только относительно мелкие осколки, породившие болиды, но и крупные, которые могут наблюдаться в виде астероидов. Поэтому есть смысл поиска других крупных фрагментов среди астероидов группы Атона.

С точки зрения динамики и физики малых тел Солнечной системы нет принципиальной разницы между астероидами групп Атона и Аполлона (q < 1 a.e., Q > 1 a.e.). По данным на сентябрь 2013 г., база данных содержит орбиты почти 5,5 тысяч астероидов из группы Аполлона. Поиск близких к Апофису орбит проводился и по этой базе.

Для поиска астероидов, возможно связанных с Апофисом, на первом этапе мы применили методику, аналогичную методике выявления метеороидных роев с использованием D-критерия Саутворта и Хокинса [18].

В метеорной астрономии считалось, что два объекта принадлежат одному метеорному рою, если значение D-критерия для их орбит не превышало 0,20. При этом предполагалось, что метеороиды, образующие рои, генетически связаны – то есть образовались при разрушении одного родительского тела. Такой вывод имеет право на существование, так как скорости разлета осколков при кометных выбросах или при столкновениях астероидов, как правило, малы по сравнению с орбитальными скоростями. Поэтому различия орбит осколков и родительского тела на начальном этапе эволюции невелики. Затем, под действием планетных возмущений и негравитационных эффектов это различие увеличивается и может стать препятствием при установлении взаимосвязи объектов. Для решения таких задач необходимо в дальнейшем исследовать эволюцию орбит на длительных интервалах времени.

Очевидно, что дисперсия элементов орбит увеличивается со временем. С этой точки зрения, чем больше различие между орбитами членов какого-либо роя, тем больше его возраст, при равенстве прочих начальных условий. С другой стороны, если поиск проводится среди большого числа орбит, то возможная близость орбит может быть случайной. Поэтому предельное значение D-критерия необходимо корректировать в соответствие с формулой (5).

В качестве исходной базы данных элементов орбит астероидов группы Атона и Аполлона использовались каталоги NASA [7, 9]. На 13 сентября 2013 г. эти каталоги содержали информацию об орбитах 786 астероидов группы Атона и 5475 орбитах группы Аполлона.

Согласно формуле (5) предельное значение DС для группы Атона составляет 0,17, а для группы Аполлона – 0,10. В результате проведенных исследований нами было найдено 30 астероидов группы Атона и 2 астероида группы Аполлона, орбиты которых отличаются от орбиты Апофиса не более чем на DС по D-критерию Саутворта и Хокинса. Элементы орбит Апофиса и объектов его роя приведены в табл. 2 вместе со значениями D-критерия, T-критерия Тиссерана и постоянных Лидова С1 и С2. В табл. 2 значения С2 даются умноженными на 100.

Представление о пространственной форме роя дают рис. 1–3. Единица масштаба на графиках составляет 1 а.е. На рис. 1 представлены орбиты 33 астероидов роя, включая Апофис, в трехмерной эклиптической гелиоцентрической системе координат. Плоскость ХоУ совпадает с плоскостью эклиптики (то есть с плоскостью орбиты Земли).

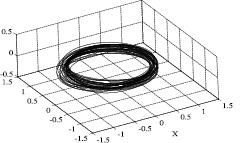
Рис. 1

Этот рисунок дает представление о пространственной форме, однако выявить рой по этому рисунку довольно сложно.

Более наглядную картину дают проекции орбит роя на плоскость эклиптики (рис. 2).

Рис. 2

Рис. 2 показывает, что орбиты астероидов роя Апофиса имеют некоторую дисперсию, которая обусловлена в основном дисперсией долгот перигелиев π. Разница в долготах вполне могла образоваться под действием планетных возмущений.

На рис. 3 представлены проекции тех же самых 33 орбит астероидов роя Апофиса, но с совмещенными направлениями на перигелии орбит. Полагалось что долготы перигелиев для всех орбит π = 0. Таким образом, выполнен качественный учет дисперсии долгот перигелиев, возникшей из-за действия планетных возмущений.

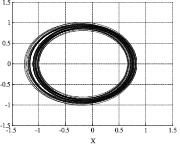
Рис. 3

Рис. 3, возможно, свидетельствует в пользу реальности существования астероидного роя Апофиса.

Таблица 2

Элементы орбит атонцев объектов роя Апофиса для которых значения D-критерия не превосходят 0,17

Рецензенты:

Заусаев А.Ф., д.ф.-м.н., профессор кафедры «Прикладная математика и информатика», Самарский государственный технический университет, г. Самара;

Кристя В.И., д.ф.-м.н., профессор кафедры прикладной математики и информатики, Институт управления, бизнеса и технологий, г. Калуга.

Работа поступила в редакцию 17.01.2014.