Многоразовая воздушно-космическая система предназначена для решения широкого круга задач в космосе, в том числе:
- Выведение на околоземную орбиту и возврат с орбиты людей и полезных грузов;
- Транспортно-техническое обеспечение космических объектов различного назначения;
- Проведение аварийно-спасательных работ на орбите;
- Проведение научно-технических и технологических экспериментов в космосе;
- Осуществление международного контроля за космическим пространством.
Создание следующих друг за другом, поколений космической техники невозможно без умения решать, наверное, самое сложное уравнение математической физики – кинетическое уравнения Больцмана.
Большую часть срока службы воздушно-космический аппарат (ВКА) находится на большой высоте, при условиях свободномолекулярного обтекания. Экспериментальные исследования таких течений (натурные и трубные) чрезвычайно сложны и дорогостоящи. Поэтому методы вычислительной аэродинамики разреженного газа в настоящее время являются практически единственным средством получения информации об аэродинамической обстановке около космического аппарата на больших высотах. Особенности исследований высотной аэродинамики связаны с тем, что при проектировании и эксплуатации ВКА необходимо рассчитывать аэродинамические характеристики (АДХ) в широком диапазоне изменения различных определяющих параметров.
Проявление методов статистического моделирования (Монте-Карло) в различных областях прикладной математики связано с необходимостью решения качественно новых задач, возникающих из потребностей практики. Метод прямого статистического моделирования является наиболее распространенным среди численных методов решения прикладных задач динамики разреженного газа [2, 6]. Метод Монте-Карло широко применяется в аэродинамике как универсальный метод расчета тел сложной формы с учетом затенения и многократных соударений с поверхностью отраженных частиц. Более того, возможности применения этого метода к расчету всего спектра течений – от сплошной среды до свободномолекулярного течения делают его все более привлекательным.
Определение граничных условий на обтекаемых разреженным газом поверхностях является одной из важнейших проблем кинетической теории газов [5]. Несмотря на значительные усилия, эта проблема до сих пор остается открытой. Взаимодействие газа с поверхностью обтекаемого тела играет определяющую роль в высотной аэродинамике [1]. Аэротермодинамические характеристики тел в потоке газа определяются передачей импульса и энергии на поверхность тела, то есть связью между скоростями и энергиями падающих на поверхность и отраженных от нее молекул, что и составляет суть кинетических граничных условий на поверхности.
Целью данной работы является определение метода вычисления АДХ ВКА в высокоскоростном потоке разреженного газа. В работе представлены результаты расчетов аэродинамических характеристик перспективных воздушно-космических аппаратов, полученные методом прямого статистического моделирования (ПСМ).
Метод и алгоритм моделирования АДХ ВКА
Развитие численных методов в динамике разреженных газов связано в первую очередь с использованием метода прямого статистического моделирования процессов, описываемых кинетическим уравнением Больцмана [2, 6, 7],
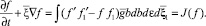
Здесь f = f(t, x, y, z, xx, xy, xz) – функция распределения молекул по времени, координатам и скоростям. f, f1, f′, f1′ – функции распределения, соответствующие скоростям пары частиц до и после столкновения, 
– относительная скорость, b – прицельное расстояние, e – азимутальный угол в плоскости, перпендикулярной плоскости столкновения. В практической реализации методы прямого статистического моделирования, основанные на подходах Бёрда [8] (моделирование динамики ансамбля молекул) и Хэвиленда [10] (моделирование индивидуальных траекторий молекул), оказались наиболее эффективными и их модификации с переменным успехом осуществляли победное шествие по вычислительной аэродинамике. Рассмотрим моделирование свободномолекулярного течения методом Монте-Карло. Алгоритм метода Монте-Карло выглядит следующим образом:
- Ввод данных.
- Выбор границы, которой стартует частица.
- Вычисление координат точки влета частицы в область.
- Вычисление скорости частицы.
- Вычисление координаты точки пересечения траектории частицы с поверхностью тела.
- Вычисление импульса и энергии, приносимых частицей.
- Вычисление скорости отраженной частицы.
- Вычисление импульса и энергии отраженной частицы.
- Выполнение пп. 4–7 до покидания молекулой расчетной области.
- Осреднение данных.
Так как частицы не сталкиваются между собой, отраженная частица либо взаимодействует с поверхностью, либо покидает расчетную область. В алгоритме происходит передача управления на пункт 1 и вычисляется траектория следующей частицы. Если тело невыпуклое или имеется несколько тел, алгоритм несколько усложняется. После пункта 8 отраженная частица может попасть на другую часть тела, поэтому управление передается на пункт 5, где вычисляются координаты точки пересечения траектории частицы с поверхностью. Если траектория частицы не пересекает тело, частица покидает область и управление передается на пункт 1.
Модели взаимодействия молекул газа с поверхностью
Роль законов взаимодействия молекул с поверхностью проявляется тем сильнее, чем более газ разрежен [5]. Граничным условиями для уравнения Больцмана являются условия, ввязывающие функцию распределения падающих и отраженных молекул [1].
В модели Максвелла плотность распределения отраженных молекул имеет вид
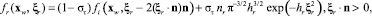
и ядро рассеяния [1, 2] имеет вид
; 
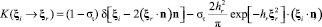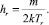
Здесь полагается, что доля (1 – st) молекул отражается зеркально, а остальная часть st молекул – диффузно, параметр 0 ≤ st + 1 определяет коэффициент аккомодации касательной компоненты импульса st = (Pti – Ptr)/Pti.
Компоненты вектора скорости при диффузном отражении моделируются в локальной сферической системе координат, ось которой направлена вдоль вектора внешней нормали к поверхности, с помощью выражений [8]
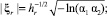
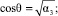
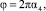
где a1, a2, a3, a4 – независимые случайные числа, равномерно распределенные в интервале (0, 1), q и j – полярный и азимутальный углы.
К. Черчиньяни и М. Лампис предложили феноменологическую модель (CL), которая также удовлетворяет принципу взаимности и является усовершенствованием максвелловской модели [9]. Модель основана на введении двух параметров, которые представляют собой коэффициент аккомодации sn = sEn по кинетической энергии, связанной с нормальной компонентой скорости, и коэффициент аккомодации касательной компоненты импульса st. Модель CL хорошо соответствует результатам лабораторных исследований с высокоскоростными молекулярными пучками [2]. Хотя сравнение ограничено лабораторными условиями, модель CL является теоретически обоснованной и относительно простой. Позднее появились модификации ядра рассеяния модели CL [12], однако они дают незначительное улучшение при сравнении с лабораторными экспериментами. В общем случае модель взаимодействия имеет несколько параметров произвольного физического смысла, которые позволяют добиться разумного согласия с результатами лабораторных исследований в некотором диапазоне условий. Универсальная модель должна использовать ядро рассеяния, полученное на основе физического эксперимента в широком диапазоне чисел Кнудсена и скоростей потока [2].
Использованное преобразование расширяет CL модель для учета обмена вращательной энергией между газом и поверхностью [12]. Модель в таком виде называется моделью Черчиньяни‒Лампис‒Лорда (CLL). Потом были предложены модификации модели [13] для учета обмена колебательной энергией и расширения диапазона состояний рассеянных молекул. Модель CLL в настоящее время получила широкое признание в работах [3, 11, 14–18].
Результаты расчетов
Рассмотрим результаты расчета коэффициентов силы сопротивления и подъемной для возвращаемого аппарата в свободномолекулярном потоке разреженного газа. Используются различные модели взаимодействия молекул с поверхностью (Максвелла и Черчиньяни‒Лампис‒Лорда, CLL). Представлены результаты расчета различным моделями взаимодействия газа с поверхностью (Максвелла и CLL) методом Монте-Карло. Значения параметров: температурный фактор tw = Tw/T∞ = 0,1; скоростное отношение s = 20; коэффициенты аккомодации тангенциального импульса и нормальной энергии στ, σn = 0,5. Расчет проводился с использованием 5·106 частиц.
Рис. 1. Геометрическое представление варианта возвращаемого аппарата
На рис. 2 представлены зависимости коэффициентов силы сопротивления Cx, подъемной силы Cy от угла атаки a от 0 до 90° для возвращаемого аппарата (рис. 1).
При уменьшении коэффициент аккомодации στ от 1 до 0.5, величина Cx увеличивается при 0° < α < 55° и значение достигает до 2,72 при α = 0°. Коэффициент Cy снижает в несколько раз по модулю при уменьшении στ от 1 до 0.5 при 0° < α < 80°. Можно объяснить, что при нулевой аккомодации все молекулы отражаются зеркально, и полной аккомодации отражаются диффузно. Зеркальные отраженные молекулы передают поверхности больший импульс, чем диффузно рассеянные от холодной стенки молекулы.
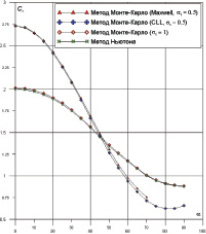
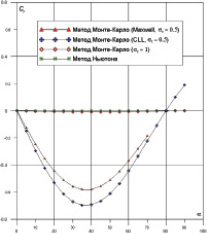
Рис. 2. Зависимости Cx(α) и Cy(α) при στ = 0,5 и 1 (tw = 0,1)
При диффузном отражении касательное напряжение от отраженных молекул равно нулю, так как при этом все направления отражения являются одинаково вероятными. Отметим, что близость результатов, полученных с помощью моделей Максвелла и CLL, отмечалась ранее в работе [14] для тел с высокими коэффициентами аккомодации поверхности, что позволяло достигнуть лучшего согласования с результатами эксперимента в аэродинамической трубе [15].
Заключение
Представлены результаты расчетов аэродинамических сил сопротивления Cx, подъемной Cy возвращаемого аппарата методом Монте-Карло при различных значениях коэффициентов аккомодации с использованием различных моделей взаимодействия молекул с поверхностью. Исследовано влияние на АДХ особенностей модели взаимодействия молекул с поверхностью. Разработанные программные системы позволяют оперативно получать АДХ разрабатываемых и эксплуатируемых ВКА на орбите и на начальном участке траектории спуска и могут быть использованы при проектировании перспективных космических аппаратов.
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Рецензенты:
Боголепов В.В., д.ф.-м.н., действительный член РАЕН, главный научный сотрудник, ФГУП ЦАГИ, профессор МФТИ, г. Жуковский.
Липатов И.И., д.ф.-м.н., чл.-корр. РАН, действительный член РАЕН, начальник отдела ФГУП ЦАГИ, профессор МФТИ, г. Жуковский.
Работа поступила в редакцию 17.01.2014.