Развитие энергетики, машиностроения, химии, транспорта в XX в. привело к тому, что человеческая деятельность стала сравнима по масштабам с естественными энергетическими и материальными процессами, происходящими в биосфере. Антропогенные воздействия приводят к нарушению практически всех природных биогеохимических циклов, в том числе включающих в себя тяжелые металлы. В настоящее время все крупные промышленные центры нуждаются в постоянном контроле выбросов, совершаемыми как стационарными, так и передвижными источниками загрязнения. Для моделирования мониторинга экологического состояния промышленного региона необходима адекватная математическая модель, следуя которой возможно не только рассчитать концентрацию загрязняющих веществ, но и строить прогноз концентраций на ближайшие периоды времени. Рассматриваемое диффузионное уравнение является одной из качественных и адекватных математических моделей для решения поставленной задачи. [1]
Пусть q(P, t) – функция, значение которой в момент времени t в точке P(x, y, z) совпадает со значениями мгновенной концентрации примеси, переносимой в атмосфере потоками воздуха. Предполагается, что функция q(P, t) непрерывно дифференцируема по x, y, z, t. Полуэмпирическое уравнение турбулентной диффузии записывают в виде [3]:
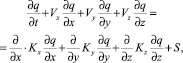(1)
где S – источник примеси, находящийся в точке P0 (x0, y0, z0) и производящий мгновенный выброс загрязняющих примесей в момент времени t0 в количестве Q0.
Для расчета средних концентраций примеси в пограничном слое атмосферы от мгновенного точечного источника используется решение уравнения (1):
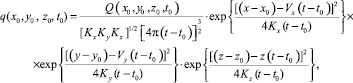(2)
называемое гауссовой функцией распределения концентрации примеси. Решение (2) получено методом функции Грина. Для расчета концентрации аэрозолей в пункте наблюдения необходимо, прежде всего, определить и задать значения исходных данных и провести нормировку основных параметров и параметризацию задачи. Исходными данными для уравнения (2) будут:
а) момент времени, когда источник производит выброс загрязняющих веществ (ЗВ) – t0;
б) координаты источника P0 (x0, y0, z0) (м);
в) расстояние от источника до пункта наблюдения R (м) – расстояние от точки P0 – источника выбросов загрязняющих веществ до точки Р – пункта наблюдения.
г) Q0 (10–3 кг/с) – количество загрязняющих веществ, выброшенное источником в начальный момент времени t0;
д) турбулентность атмосферы в пограничном слое, характеризуемая коэффициентом турбулентной диффузии К = {Kx, Ky, Kz} (м2/с);
е) скорость ветра V = {Vx, Vy, Vz} (м/с).
Помимо исходных данных необходимо также вычислить следующие параметры задачи: координаты пункта наблюдения Р, в котором проводятся замеры концентрации загрязняющих веществ, поступающих от источника:
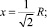
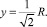(3)
Далее проводим нормирование переменных задачи. Положим, что
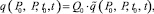(4)
где
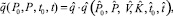(5)
, 
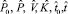– нормированные величины, принимающие значения в интервале (0,1). Пронормируем переменные и распределения задачи следующим образом: 
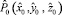, где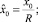 
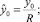
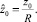Аналогично получаем 
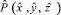, где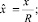 
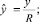
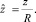Коэффициенты турбулентной диффузии и скорости ветра пронормируем как обычно:
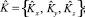
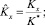
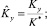
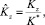(6)
где K* = max{Kx, Ky, Kz};
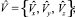
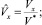
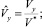
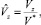(7)
где V* = max{ Vx, Vy, Vz }.
Далее нормируем переменные
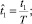
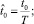
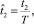
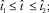(8)
T = t* – t0 – временной интервал, в течение которого в пункт наблюдения будут поступать загрязнения.
С учетом вышеизложенного уравнение (5) можно записать таким образом:
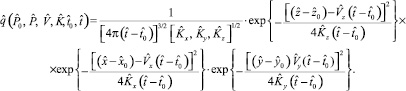(9)
Рассмотрим случай, когда в точке P0 (x0, y0, z0) работает источник в течение конечного промежутка времени [ζ, ζ0 + T] и в точке наблюдения Р(x, y, z) происходит процесс накопления загрязняющих веществ. Предполагается, что в пункте наблюдения ведутся замеры (прием) концентрации поступивших примесей от источников в моменты времени t ∈ [t1, t2]. Функция S(P0, ζ) имеет смысл интенсивности источника, при этом функция S(P0, ζ) Δζ (10–3 кг/м3) определяет количество вещества, выброшенного в атмосферу за элементарный интервал времени Δζ в окрестности ζ. Согласно рассмотренной теории, импульс возмущения загрязняющих веществ S(P0, ζ) будет приниматься в точке Р в интервале [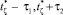
]. В силу этого начальное возмущение S(P0, ζ) будет приниматься в точке Р во время 
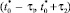, а последнее – во время 
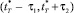. Объединение этих интервалов дает интервал 
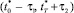. Таким образом, становится видно, что интервал [ζ, ζ0 + T] соответствует интервалу 
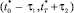. Моменты времени ζ и 
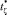связаны простым преобразованием:
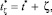(10)
и, следовательно, интервал [ζ, ζ0 + T] соответствует интервалу
ζ0 + t* – τ1 ≤ t ≤ ζ0 + T + t* + τ2.
В итоге имеем:
ζ0 + t* – τ1 ≤ t ≤ ζ0 + T + t* + τ2. (11)
Неравенство (11) определяет время возможного приема импульса возмущения загрязняющих веществ или, иными словами, время прохождения импульса возмущения загрязняющих веществ через точку Р – пункт наблюдения.
Теперь нужно построить интегральную форму Q(P0, P, t), определяющую количество загрязняющих веществ, накопившееся за время работы источника в точке Р. Для этого выберем на интервале [ζ, ζ0 + T] точку ζk и интервал Δζk следующим образом:
ζk = ζ0 + k∆ζ, (12)
где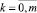 
и ∆ζk = ζk + 1 – ζk.
Введем в рассмотрение точку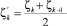 
и примем в точке P0 выброс:
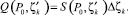(13)
Тогда в точке Р реакция будет следующей: [3]
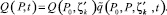(14)
В итоге можно записать:
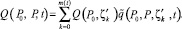(15)
Это интегральная сумма, остается перейти к пределу при ∆ζ → 0 и сделать замену m(t) → ζ(t), получим:
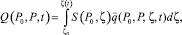(16)
где ζ0 ≤ ζ < ζ0 + T,
ζ0 + t* – τ1 ≤ t ≤ ζ0 + T + t* + τ2
или t1 ≤ t ≤ t2, если принять
t1 = ζ0 + t* – τ1;
t2 = ζ0 + T + t* + τ2; ζ(t) = t – t*. (17)
Далее рассмотрим вариант, когда источник работает непрерывно, а в точке Р фиксируется количество загрязняющих веществ в течении определенного промежутка времени [t1, t2]. Необходимо определить
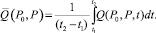(18)
Выражение (18) задает усредненное значение концентрации загрязняющих веществ, приходящееся на один кубический метр и накопившееся за время [t1, t2]. В данном случае интервал [t1, t2] задан и требуется определить соответствующий ему интервал [ζ1, ζ2]. Согласно (13) t1 = ζ0 + t* – τ1, t2 = ζ0 + T + t* + τ2. Отсюда находим ζ0 = t1 + τ1 – t* и ζ0 + T = t2 – t* – τ2. Обозначим ζ1 = ζ0 и ζ2 = ζ0 + T. В результате получаем ζ1 = t1 + τ1 – t* и ζ2 = t2 – t* – τ2. В итоге имеем следующие расчетные формулы:
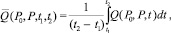(19)
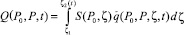(20)
ζ1 = t1 + τ1 – t*;
ζ2 = t2 – t* – τ2; t1 ≤ t ≤ t2. (21)
Проведем расчет концентрации примесей, поступающих в точку наблюдения от источника согласно методике (16), (18). Для этого необходимо, прежде всего, задать исходные данные и провести нормировку основных переменных и полей задачи. Затем необходимо вычислить прихода Р – максимума загрязняющих веществ, поступающих от источника. Затем задаем разбиение отрезка [t1, t2] и формируем массив {tl},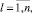 
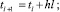
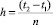[4]. После нормирования переменных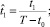 
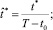
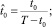
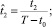
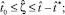
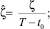dζ = (T – t0), 
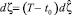можно записать:
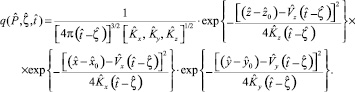(22)
Далее рассмотрим функцию источника. Допустим, что
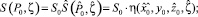(23)
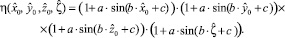
В итоге имеем [3]:
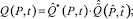(24)
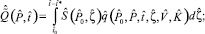(25)
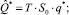S0 = Q0. (26)
Таким образом, показана возможность практического применения разработанной расчетно-аналитической методики оценки концентрации загрязняющих веществ к прикладным задачам оперативного контроля состояния промышленного региона, что позволяет осуществить его экологический прогноз [1]. Таким образом, показана возможность практического применения разработанной расчетно-аналитической методики оценки концентрации загрязняющих веществ к прикладным задачам оперативного контроля состояния промышленного региона, что позволяет осуществить его экологический прогноз.
Рецензенты:
Джомартова Ш.А., д.т.н., профессор, кафедра «Информационные системы», механико-математический факультет, Казахский национальный университет имени аль-Фараби, г. Алматы;
Дауылбаев М.К., д.ф.-м.н., кафедра дифференциальных уравнений и теории управления, механико-математический факультет, Казахский национальный университет имени аль-Фараби, г. Алматы.
Работа поступила в редакцию 17.01.2014.