При исследовании надежности и долговечности деталей и узлов молота возникает необходимость в определении действующих нагрузок. Прочность деталей молота, качественные показатели этой машины зависят от силы сопротивления поковки деформированию. Доказано, что динамический расчет частей ковочного молота без учета деформации заготовки совершенно недопустим [1].
Подавляющее большинство заготовок перед дальнейшей ковкой проходит операцию осадки, при которой в результате продольного удара увеличивается площадь поперечного сечения заготовки за счет уменьшения ее высоты.
Высокие уровни нагружения вызывают в заготовках ковочных молотов значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации, которые и составляют осадку. Т.е. в заготовках имеют место вязкоупругие деформации.
Таким образом, падающие части ковочного молота в процессе ударного взаимодействия с заготовкой можно моделировать сложной вязкоупругой стержневой системой с распределенными параметрами, соударяющейся с препятствием.
Заготовка, обладающая одновременно упругостью, вязкостью и пластичностью в различных формах и соотношениях, моделируется в виде вязко-упругого тела Максвелла. Учет рассеяния энергии осуществляется согласно [5].
Для вязко-упругого элемента Максвелла существуют следующие зависимости:
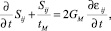
где tM – время релаксации напряжений; Sij – тензор напряжений; εij – тензор деформаций.
Вводя параметр преобразования Лапласа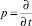 
, и учитывая, что при построении АФЧХ p = iω получим:
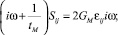
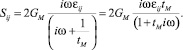
Откуда получаем выражения для характеристики E:
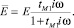
Коэффициент tM определяется экспериментальным путем.
Детали молота моделируются упругой стрежневой системой с распределенными параметрами, испытывающей ударные нагрузки. Подкладка под шаботом, состоящая из дубовых брусьев, моделируется упругим основанием с сосредоточенной жесткостью с в соответствующих узлах системы. Поскольку соединение верхнего бойка с бабой, нижнего бойка с подушкой и подушки с шаботом осуществляется фигурным пазом типа «ласточкин хвост», то контактное взаимодействие таких стыков можно моделировать пружиной. Методика расчета контактных деформаций стыков с учетом реальных условий заимствована из работы [2].
Рассмотрим для примера паровоздушный ковочный молот арочного типа модели М1345 (рис. 1).
Рассмотрим частотный метод динамического расчета нестационарных колебаний ковочного молота в процессе ударного взаимодействия с заготовкой. Предлагаемая методика использует модификацию метода конечных элементов (МКЭ), основанную на точном интегрировании дифференциального уравнения для конечного элемента [3] и позволяет рассчитывать продольные и поперечные колебания стержней ступенчато-переменного сечения с учетом или без учета рассеяния энергии при соударении с жестким препятствием [4].
Предлагаемый подход справедлив для стержней неограниченной длины, поэтому разбиение на участки молота можно проводить в любых сечениях, но наиболее целесообразно там, где меняются физические или геометрические характеристики объекта. При составлении расчетной схемы молота считалось, что в штоке, бабе, бойках, подушке и верхней части шабота возникают продольные колебания, а в основании шабота – поперечные.
Таким образом, расчетная схема ковочного молота (рис. 1) будет состоять из 19 узлов. Участки 7–8, 12–13 и 14–15 моделируют стыки. Узлы 17, 18 и 19 имеют упругое основание, заменяющее влияние подкладки из дубовых брусьев. На участках между 1 и 18 узлом имеют место продольные колебания, а на участках 17–18 и 18–19 – поперечные. На завершающей стадии удара верхний боек считается присоединившимся к заготовке (рис. 1).
Предлагаемой расчетной схеме соответствует следующая система разрешающих уравнений для построения амплитудно-фазо-частотных характеристик (АФЧХ) перемещений:
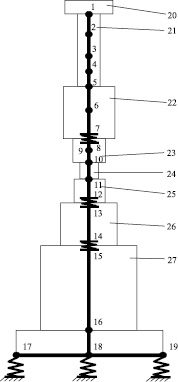
Рис. 1
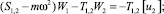
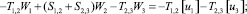
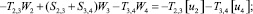
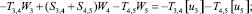
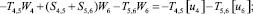
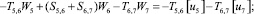
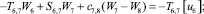
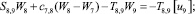
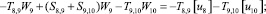
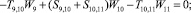
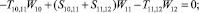
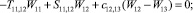
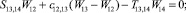
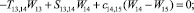
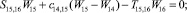
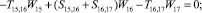
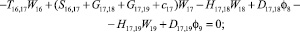
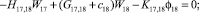
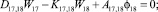
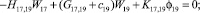
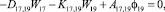
где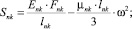 
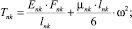
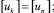
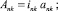
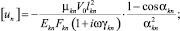
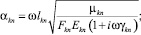
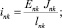
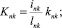
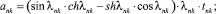
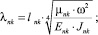
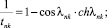
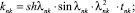
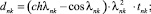
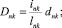
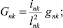
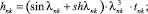
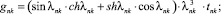
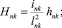
n, k – индексы, указывающие соответственно начало и конец участка; j – номер узла (i = 1,2…19); i – мнимая единица,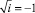 
; Jnk – осевой момент инерции сечения участка nk, м4; Еnk – модуль упругости участка nk, Па; Fnk – площадь поперечного сечения участка nk, м2; lnk – длина участка nk, м; µnk – масса единицы длины стержня участка nk, кг/м; V0 – скорость соударения с заготовкой, м/с; γnk – коэффициент сопротивления участка nk; ω – частота колебаний, с–1; Wj – перемещение j-го узла, м; ϕj – угол поворота j-го узла, рад; сj – жесткости пружин, моделирующих упругое основание в j-м узле, кг/м; сnk – жесткости пружин, моделирующих стыки nk, кг/м .
Из этой системы находятся изображения перемещений в узлах системы. Зная перемещения начала и конца стержня, рассчитываются продольные усилия Ni(ω) (рис. 2). Переходя к оригиналам N(t), находятся напряжения σ(t) и деформации ε(t), которые связаны с усилиями следующими зависимостями:
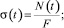
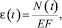
где σ(t) – напряжение, Па; N(t) – продольная сила, Н; t – время, с; ε(t) – деформации, м; F – площадь поперечного сечения, м2; Е – модуль упругости, Па.
В ходе исследований выявлен информативный диапазон частот, позволяющих идентифицировать получаемые АФЧХ. Для этого провели анализ спектра колебаний падающих частей молота при жестком ударе и при ударе о заготовки различных размеров и материалов с разными скоростями соударения в диапазоне частот от 0 до 500 с–1 в различных узлах стержневой системы.
а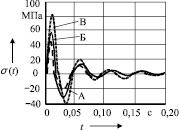 
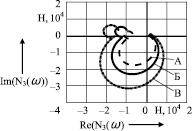
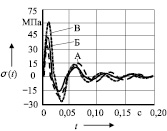
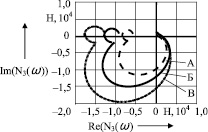
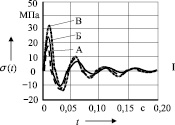
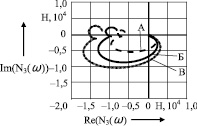
Рис. 2
Все дальнейшие вычисления проводятся в выявленном информативном диапазоне частот. При этом материал поковки существенно не влияет на указанный диапазон частот, вызывая лишь некоторое увеличение резонансной частоты по мере уменьшения модуля упругости Е и коэффициента сопротивления материала поковки γ. Так, при жестком ударе значение резонансной частоты в месте заделки штока в бабу составило 160 с–1, для поковки из стали 45 (Е = 2,1⋅1011 Па, ρ = 7850 кг/м3, γ = 0,01) – 204 с–1, для титанового сплава ОТ4 (Е = 1,03⋅1011 Па, ρ = 7000 кг/м3, γ = 0,01) – 223 с–1, а для алюминиевого сплава АК6 (Е = 1,05⋅1011 Па, ρ = 2700 кг/м3, γ = 0,007), обладающего меньшим пределом прочности – 250 с–1.
а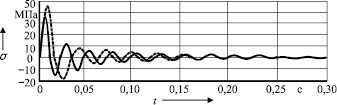 
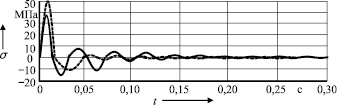
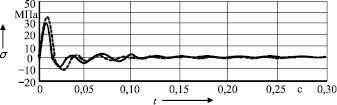
Рис. 3
К изменяемым параметрам при работе молота относятся скорость соударения, материал и размеры поковки. Теоретические исследования следующего этапа показали, что на напряжения, возникающие в различных узлах системы при соударении падающих частей с заготовкой, влияют все вышеперечисленные параметры (рис. 2).
Результаты сравнения теоретических и экспериментальных результатов показали, что средняя погрешность вычислений составляет 14 % (рис. 3), что свидетельствует об адекватности построенных математических моделей и достаточной точности предлагаемого способа определения напряжений в заготовке при ковке.
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск;
Антонец И.В., д.т.н., профессор Ульяновского государственного технического университета, г. Ульяновск.
Работа поступила в редакцию 17.01.2014.